复变：认识复数

本文主要参考视频：

2.4.解析函数：解析函数与调和函数_哔哩哔哩_bilibili

仅复习一些基础内容，供本人学习之用。

另外有一篇文章说的挺有意思，可以看看：

数字——虚数概述 - 知乎 (zhihu.com)

虚数单位和复数

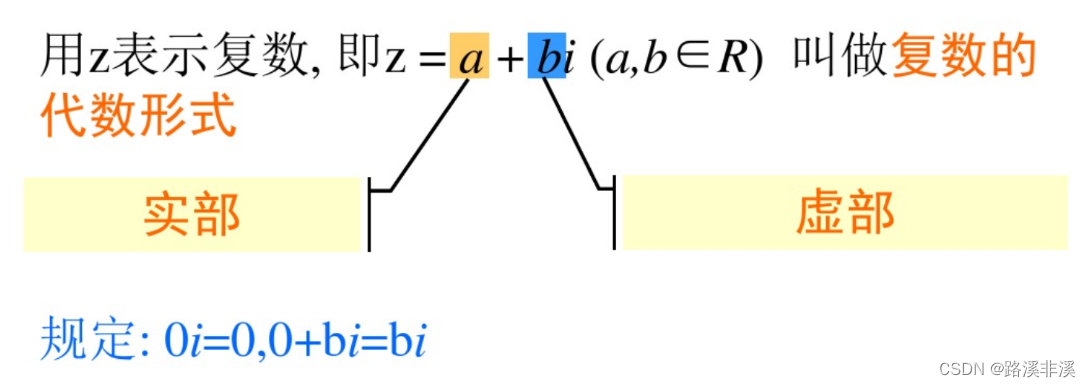
复数的表示方法

复数有三种表示方法

向量表示式

向量表示中，有一些概念需要搞清楚

Arg，argument，辐角

如果只看辐角，那么范围是无限的，因为转一圈2π，转k圈就是2kπ……

所以，我们一般都是看主值，范围在-π到π之间

三角表示式

 

这个公式很好理解，对于z=x+iy来说，x就是复数构成的三角形的θ角的邻边，y就是对边，又有复数的模r是斜边的长度，根据三角函数的定义，有x=rcosθ，y=rsinθ，带入得z=r*cosθ+r*isinθ，把r提出来，就是z=r(cosθ+isinθ)

指数表示式

学习指数表示式之前，得熟悉下“欧拉公式”

总结如下：

上小节我们知道了复数的三角表示式z=r(cosθ+isinθ)

显然，括号里可以使用欧拉公式变成e^iθ

因此，复数可以使用指数来表示为

z=re^iθ

更加简洁。

复数的运算

交换律、结合律和分配率

复数的共轭和四则运算

注意，相除时分母上的虚数部分通过同时乘以分母的共轭，来将虚数单位给化掉了。

复数的乘幂和方根

复数运算的几何意义

加减的几何意义

乘积和商的几何意义

注意，这里是模相乘，不是什么系数相乘。

比如i*i，模相乘得1，角度相加得π，最后结果是-1

下面的内容暂时做个简单了解即可。 

---

复变函数

注意，这里是写成了实部和虚部的标准形式。

复变函数的极限

复变函数的连续性

解析函数

柯西-黎曼方程

函数在某点可导的充要条件

求导公式

解析

初等函数

这里的初等函数指的是复数的初等函数