笔记：ML-LHY-6 Brief Introduction of Deep Learning-CSDN博客

本文链接：https://blog.csdn.net/qq_29598161/article/details/107525351

从1958年感知机的提出到2012年AlexNet在图像竞赛中的突破，深度学习经历了一系列关键进展。课程涵盖神经网络、反向传播、受限玻尔兹曼机等核心概念，探讨了深度模型的必要性和GPU加速的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

这节课主要介绍介绍了深度学习的发展，神经网络概念，层的作用
pdf 视频

Deep Learning 发展

1958：感知机(线性模型，和Logistic Regression非常像，没有sigmoid)
1969：发现感知机的限制
1980s：多层感知机(和现在的深度学习方法没有明显区别)
1986：反向传播(发现超过3层隐藏层没有帮助)
1989：发现1个隐藏层就可拟合任何函数，为什么需要深度(多层隐藏层)
2006：使用受限玻尔兹曼机(RBM)初始化(和多层感知机的区别就是有无使用RBM初始化然后进行GD，RBM使用图模型并且复杂，但是提升似乎不够明显)，使用了RBM初始化被称为Deep Learning
2009：GPU加速(矩阵运算)
2011：开始使用Deep Learning进行语音识别
2012：ALexNet在ILSVRC图像竞赛中取得很好的性能

Deep Learning 步骤

和Logistic Regression一样定义函数结构、找最好的模型(损失的定义)、得到最好的结果(梯度下降)

定义函数结构

Deep Learning的函数结构就是Neural Network
在这里插入图片描述

在这里插入图片描述

这里可以用上节最后的多个Logistic Regression来理解，神经元的输入可以是上层神经元的输出
在这里插入图片描述
这里的激活函数还是Sigmoid函数： $\sigma(z)=\frac{1}{1+e^{-z}}$ ，上图有2个隐藏层,1个输入层和1个输出层。因为层和上一层的神经元是全连接的（一个神经元输出连接到下一层所有神经元上，下一层的神经元把上一层所有神经元的输出作为输入），并且传递时正向的，所以叫做全连接正向网络(Fully Connect Feedforward Network)
上图表示为函数形式的输入和输出：

$f\left(\left[\begin{array}{c} 1 \\ -1 \end{array}\right]\right)=\left[\begin{array}{l} 0.62 \\ 0.83 \end{array}\right] \quad f\left(\left[\begin{array}{l} 0 \\ 0 \end{array}\right]\right)=\left[\begin{array}{l} 0.51 \\ 0.85 \end{array}\right]$

多个特征(输入特征 $x_1,x_2...x_n$ )和层次划分：
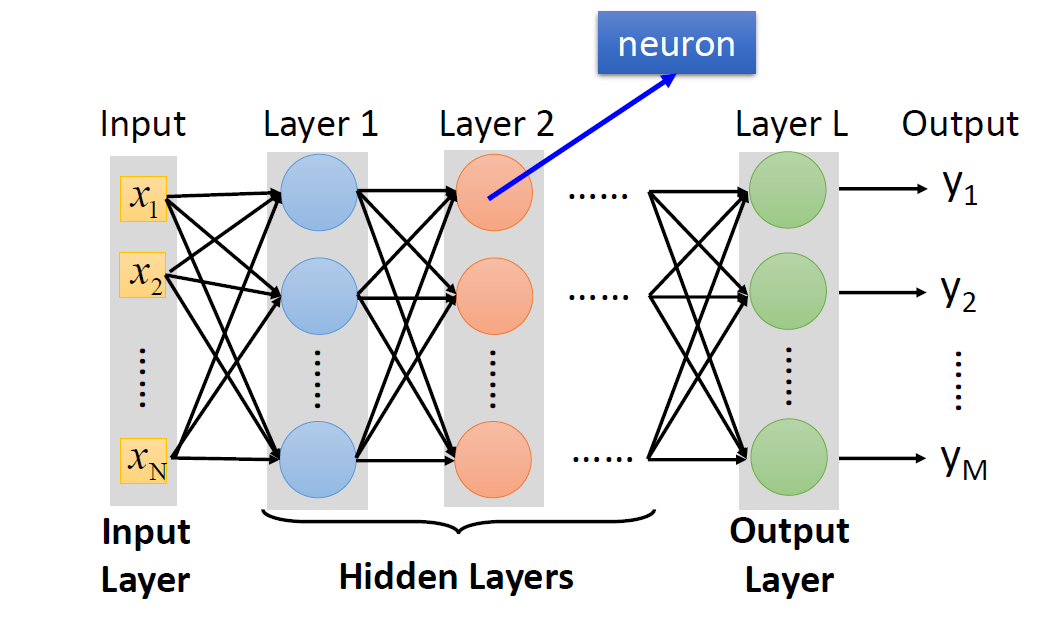
在这里插入图片描述

层数对比：
在这里插入图片描述
各个模型paper笔记：ALexNet、VGG、GoogLeNet、Residual Net

表示为矩阵操作

在这里插入图片描述
然后
$y = f (x)$
就可以表示为：
$\left.\left.\left.f(x)=\sigma\left(\begin{array}{ccccccccc} W^{L} & \cdots & \sigma( & W^{2} & \sigma( & W^{1} & x & + & b^{1} \end{array}\right)+b^{2}\right) \cdots+b^{L}\right)\right)$