[今日Arxiv] LLM推理中的错误自迭代改进，DeepMind_when can llms actually correct their own mistakes?-CSDN博客

本文链接：https://blog.csdn.net/qq_29883477/article/details/142263153

最近思维链微调范式很火，翻出来DeepMind的文章分享出来。

大致讲了推理过程中的自改进迭代思路，注重推理过程。

来自 1UC Berkeley, 2Google DeepMind, ♦Work done during an internship at Google DeepMind 的文章

文章标题：

Scaling Llm Test-Time Compute Optimally Can Be More Effective Than Scaling Model Parameters

URL：https://arxiv.org/abs/2408.03314

注：翻译可能存在误差，详细内容建议查看原始文章。

摘要

使LLM能够通过使用更多测试时间计算来改进其输出是朝着构建普遍自改进代理的关键一步，这些代理可以在开放的自然语言上操作。在这篇论文中，我们研究了推理时间计算在LLMs中的扩展性，重点在于回答这个问题：如果一个 LLM被允许使用固定但非微不足道的推理时间计算量，它能在多大程度上提高其在挑战性提示下的性能？回答这个问题不仅对实现LLM的性能有影响，而且对未来预训练和如何权衡推理时间和预训练计算也有影响。尽管它很重要，但很少有研究试图理解各种测试时间推理方法的扩展行为。此外，目前的工作主要为这些策略提供负面结果。在这项工作中，我们分析了两种扩测试时间计算的主要机制：(1)针对密集、基于过程的验证奖励模型进行搜索；以及(2)根据提示在测试时间时适应性地更新模型对响应的分布。我们发现，在这两种情况下，扩测试时间计算效果的不同方法的有效性在很大程度上取决于提示难度。这一观察结果激发了“最优运算”缩放策略的应用，该策略以每种提示最有效地分配测试时间计算的方式运行。通过使用这种最优运算策略，我们可以将测试时间计算缩放的效率提高4倍以上与最佳N基线相比。
此外，在浮点操作匹配评估中，我们发现对于基础模型在其中取得某种程度非微不足道成功率的问题，可以利用测试时间计算超越14倍更大的模型。

Enabling LLMs to improve their outputs by using more test-time computation is a critical step towards building generally self-improving agents that can operate on open-ended natural language. In this paper, we study the scaling of inference-time computation in LLMs, with a focus on answering the question: if an LLM is allowed to use a fixed but non-trivial amount of inference-time compute, how much can it improve its performance on a challenging prompt? Answering this question has implications not only on the achievable performance of LLMs, but also on the future of LLM pretraining and how one should tradeoff inference-time and pre-training compute. Despite its importance, little research attempted to understand the scaling behaviors of various test-time inference methods. Moreover, current work largely provides negative results for a number of these strategies. In this work, we analyze two primary mechanisms to scale test-time computation: (1) searching against dense, process-based verifier reward models; and (2) updating the model's distribution over a response adaptively, given the prompt at test time. We find that in both cases, the effectiveness of different approaches to scaling test-time compute critically varies depending on the difficulty of the prompt. This observation motivates applying a "compute-optimal" scaling strategy, which acts to most effectively allocate test-time compute adaptively per prompt. Using this compute-optimal strategy, we can improve the efficiency of test-time compute scaling by more than 4× compared to a best-of-N baseline.Additionally, in a FLOPs-matched evaluation, we find that on problems where a smaller base model attains somewhat non-trivial success rates, test-time compute can be used to outperform a 14× larger model.

1. 介绍

1. Introduction

人类倾向于在难题上思考更长的时间，以可靠地提高他们的决策([9, 17, 18])。

我们能否将类似的能力注入到当今的大型语言模型(LLM)中呢？更具体地说，面对一个棘手的输入问题时，我们是否能够使语言模型在测试阶段最有效地利用额外的计算能力，从而提升其回答的准确性？理论上讲，在测试时应用额外的计算应能使LLM的表现超过其训练时所达到的水平。此外，这种测试时间的能力还有望在代理性和推理任务中开拓新的途径([28, 34, 47])。例如，如果预训练模型大小可以与推理过程中的额外计算进行权衡，这将允许在实际使用场景中部署LLM，在这些场景中，可以使用较小的设备上模型代替数据中心级别的大语言模型。通过利用测试时的计算自动化提升模型输出质量，也为实现一个能在减少人类监管的情况下自主进化的通用算法提供了途径。

先前研究推理时间计算的研究提出了混合结果。一方面，一些研究表明当前的LLM能够通过测试阶段的计算改进其输出([4, 8, 23, 30, 48])，另一方面，其他研究表明这些方法在如数学推理等更复杂任务上的有效性仍然高度有限([15, 37, 43]) ，即使推理问题往往需要对现有知识而非新知识进行推断。这类矛盾的发现促使我们有必要系统地分析各种扩展测试期计算能力的方法。

Humans tend to think for longer on difficult problems to reliably improve their decisions [9, 17, 18].

Can we instill a similar capability into today's large language models (LLMs)? More specifically, given a challenging input query, can we enable language models to most effectively make use of additional computation at test time so as to improve the accuracy of their response? In theory, by applying additional computation at test time, an LLM should be able to do better than what it was trained to do. In addition, such a capability at test-time also has the potential to unlock new avenues in agentic and reasoning tasks [28, 34, 47]. For instance, if pre-trained model size can be traded off for additional computation during inference, this would enable LLM deployment in use-cases where smaller on-device models could be used in place of datacenter scale LLMs. Automating the generation of improved model outputs by using additional inference-time computation also provides a path towards a general self-improvement algorithm that can function with reduced human supervision.

Prior work studying inference-time computation provides mixed results. On the one hand, some works show that current LLMs can use test-time computation to improve their outputs [4, 8, 23, 30, 48], on the other hand, other work shows that the effectiveness of these methods on more complex tasks such as math reasoning remains highly limited [15, 37, 43], even though reasoning problems often require drawing inferences about existing knowledge as opposed to new knowledge. These sorts of conflicting findings motivate the need for a systematic analysis of different approaches for scaling test-time compute.

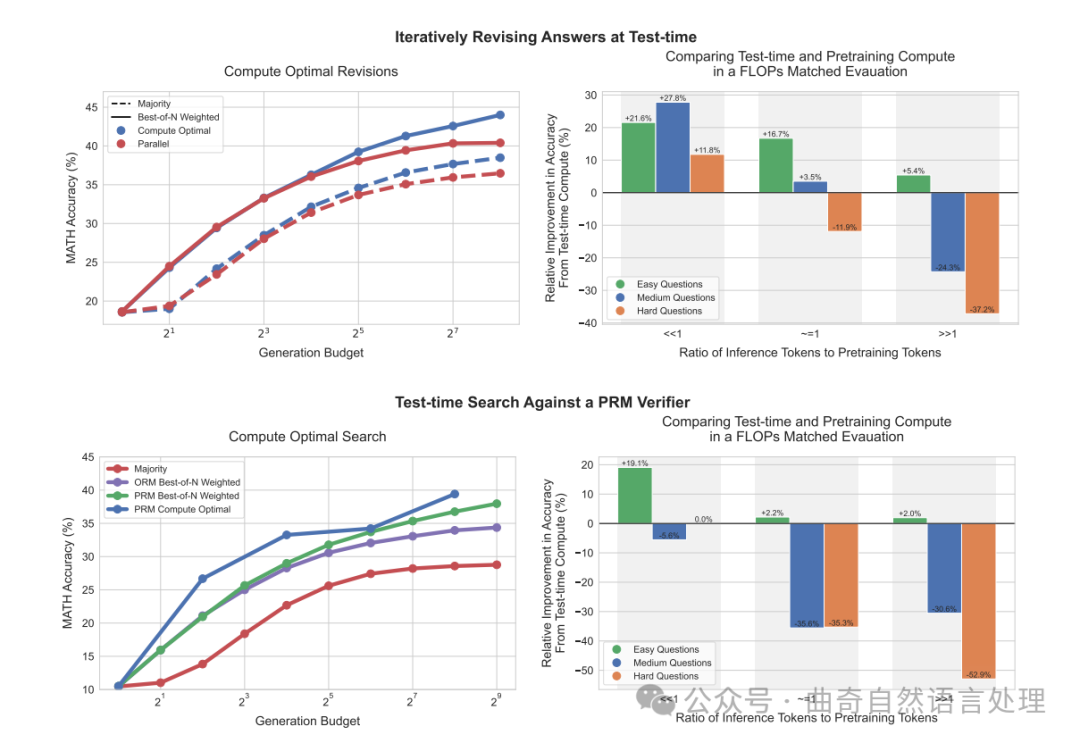
图1 ∣ 我们主要结果的概述. 左：迭代自优化（即，修订）和搜索的计算最优缩放策略。 在左边，我们将PaLM 2-S修订模型的计算最优缩放策略与基线在修订设置（顶部）以及PRM搜索设置（底部）下进行比较。我们发现，在修订情况下，标准的最好的N个策略（例如，“并行”）和计算最优缩放之间的差距逐渐扩大，使得计算最优缩放能够以4倍少的测试时间计算量超越最佳的N个策略。同样地，在PRM搜索设置下，从计算最优缩放中我们观察到对最好N个策略显著的早期改善，几乎在某些点上以4倍。较少的计算量超过最好的N个策略。具体细节请参阅第5和6节。右：比较测试时间计算量与模型参数缩放。 我们将PaLM 2-S的计算最优测试时间缩放性能与一个大约14倍大的预训练模型相比，该模型没有额外的测试时间计算（例如，贪婪采样）。我们考虑的是每个模型期望有的预训练标记和的推理标记的情况。通过训练更大的模型，我们实际上增加了这两项FLOPs要求。如果我们对较小的模型应用额外的测试时间计算量，以匹配这个更大模型的FLOPs要求，那么在准确性方面会有什么比较结果？我们发现，在修订（顶部）时当 << 时，测试时间计算对于较易的问题通常是更优的选择。然而，随着推理与预训练标记比率的增加，测试时间内计算在简单问题上仍然是优选的。而在难度较大的问题上，则预训练更为可取。我们在PRM搜索（底部)中也观察到了类似的趋势。更多细节请参阅第7节。

我们有兴趣理解增加测试阶段计算的好处。可以说，最简单且研究最为透彻的扩大测试阶段计算的方法是最佳N选一采样：从基础LLM平行地采样N个输出，并依据学习到的验证器或奖励模型选出分数最高的一个[7, 22]。然而，这种方法并非利用测试阶段计算提升LLM性能的唯一途径。通过修改获取响应的提议分布(例如，要求基础模型“依次”修正其原始响应[28])，或是改变验证器的使用方式(例如，训练基于过程的密集型验证器，并针对此验证器进行搜索[22, 45])，如我们在论文中所示，测试阶段计算的能力可能大幅提高。

为了理解增加测试阶段计算的好处，我们对具有挑战性的MATH[13]基准进行了实验，使用了PaLM-2[3]模型，这些模型特别微调至能够修订。在MATH上，需要进行特定于能力的微调，才能将修订和验证能力引入到基础模型中。

We are interested in understanding the benefits of scaling up test-time compute. Arguably the simplest and most well-studied approach for scaling test-time computation is best-of-N sampling: sampling N outputs in "parallel" from a base LLM and selecting the one that scores the highest per a learned verifier or a reward model [7, 22]. However, this approach is not the only way to use test-time compute to improve LLMs. By modifying either the proposal distribution from which responses are obtained (for instance, by asking the base model to revise its original responses "sequentially" [28]) or by altering how the verifier is used (e.g. by training a process-based dense verifier [22, 45] and searching against this verifier), the ability scale test-time compute could be greatly improved, as we show in the paper.

To understand the benefits of scaling up test-time computation, we carry out experiments on the challenging MATH [13] benchmark using PaLM-2 [3] models specifically fine-tuned1to either revise
1Capability-specific finetuning is necessary to induce revision and verification capabilities into the base model on MATH

对于错误答案[28]（例如，改进提议分布；第6节）或使用基于过程的奖励模型(PRM)[22, 45]（第5节）验证答案中各个步骤的正确性，在这两种方法下，我们发现某个特定测试时间计算策略的有效性在很大程度上取决于手头具体问题的本质以及采用的基础LLM。例如，在基础LLM已经能够轻松产生合理响应的较易问题上，允许模型通过预测N次修订序列（即，修改提议分布）迭代优化其初始答案，可能比并行采样N个独立响应更有效利用测试时间计算资源。反之，在需要探索许多不同解题高级策略的更难题目中，并行重新采样新的独立响应或利用基于过程的奖励模型进行树搜索，可能是更为有效的使用测试时间计算的方式。这一发现突显了采用适应性的“计算最优”策略来扩展测试时间计算的需求——其中具体运用测试时间计算的方法取决于提示内容以获得最优化的资源利用。我们还展示了从基础LLM的角度出发对问题难度（第4节）的概念，可以预测测试时间计算的有效性，使我们在接收到一个提示时能够实质上实现“计算最优”的策略。通过妥善分配测试时间计算资源，我们能够在很大程度上改善测试时间计算的扩展能力，在仅使用大约4倍较少的计算量下超越N选最佳基准（结合修订和搜索）的表现；见第5与6节。

利用我们改进的测试时间计算扩展策略，我们的目标是探究在多大程度上，测试时间计算可以有效地替代额外预训练。我们在较小模型加上额外测试时间计算资源与14倍更大的模型进行等量运算符（FLOPs）对比分析。我们发现，在较易和中间难度问题上，甚至在硬性问题上（具体取决于对预训练与推理工作负荷的特定条件），额外的测试时间计算往往优于扩展预训练规模。这一发现表明，在某些情况下，专注于扩大模型尺寸以进行更多预训练不如先采用较小的模型进行较少计算资源的预训练，再通过增加测试时的计算来提升模型输出效果。尽管如此，对于最具挑战性的问题，我们发现在提升测试时间计算方面所获得的好处非常有限。相反地，在这些问题上，我们发现增加额外预训练计算量更有效促进进展，这表明当前的测试时间计算扩增策略与扩大预训练规模可能并非可一比一转换。总体而言，即使采用相对朴素的方法，升级测试时计算资源已经显现出优于加大预训练的优势，且随着测试时间策略的完善将进一步提升效果。长远来看，这暗示了未来可能会减少在预训练阶段花费的FLOPs数量，而将更多FLOPs用于推理阶段。

incorrect answers [28] (e.g. improving the proposal distribution; Section 6) or verify the correctness of individual steps in an answer using a process-based reward model (PRM) [22, 45] (Section 5). With both approaches, we find that the efficacy of a particular test-time compute strategy depends critically on both the nature of the specific problem at hand and the base LLM used. For example, on easier problems, for which the base LLM can already readily produce reasonable responses, allowing the model to iteratively refine its initial answer by predicting a sequence of N revisions (i.e., modifying the proposal distribution), may be a more effective use of test-time compute than sampling N independent responses in parallel. On the other hand, with more difficult problems that may require searching over many different high-level approaches to solving the problem, re-sampling new responses independently in parallel or deploying tree-search against a process-based reward model is likely a more effective way to use test-time computation. This finding illustrates the need to deploy an adaptive "compute-optimal" strategy for scaling test-time compute, wherein the specific approach for utilizing test-time compute is selected depending on the prompt, so as to make the best use of additional computation. We also show that a notion of question difficulty (Section 4) from the perspective of the base LLM can be used to predict the efficacy of test-time computation, enabling us to practically instantiate this 'compute-optimal' strategy given a prompt. By appropriately allocating test-time compute in this way, we are able to greatly improve test-time compute scaling, surpassing the performance of a best-of-N baseline while only using about 4x less computation with both revisions and search (Sections 5 and 6).

Using our improved test-time compute scaling strategy, we then aim to understand to what extent test-time computation can effectively substitute for additional pretraining. We conduct a FLOPs-matched comparison between a smaller model with additional test-time compute and pretraining a 14x largermodel. We find that on easy and intermediat