【图论】系列（二）图的连通性

愷创作者

已于 2025-01-15 16:33:00 修改

阅读量902

点赞数 20

分类专栏：图论系列文章标签：图论人工智能网络

于 2025-01-15 11:25:14 首次发布

本文链接：https://blog.csdn.net/qq_30066733/article/details/145130924

版权

图论系列专栏收录该内容

10 篇文章 ¥19.90 ¥99.00

订阅专栏

与矩阵有关的衡量图的连通性的所有指标

1、邻接矩阵（Adjacency Matrix）

邻接矩阵的幂次可以帮助判断图的连通性。通过计算邻接矩阵的高次幂（例如 ${A^k}$ ），如果图是连通的，任意两点之间都有路径。

强连通性的作用：

如果图是强连通的，任意两个节点之间应该存在路径。如果图是强连通的，可以通过邻接矩阵的高次幂来验证：
- 如果图是强连通的，那么存在一个整数k，使得邻接矩阵的高次幂 ${A^k}$ 中所有元素都大于零。这意味着通过
  𝑘 步路径，从任意节点可以到达所有其他节点。
如果 ${A^k}[i][j] > 0$ 表示从节点 𝑖可以通过 𝑘步路径到达节点 j，且对任意的 i,j 都成立，说明图是强连通的。

2、拉普拉斯矩阵（Laplacian Matrix）

拉普拉斯矩阵 L 是图的另一种矩阵表示，广泛应用于图的分析和连通性研究。

定义：拉普拉斯矩阵是图的度矩阵减去邻接矩阵，即：
无向图 $L = {D} - A$
其中，D 是度矩阵，矩阵的对角线元素表示每个节点的度数，非对角线元素为零。
有向图 $L = {D_{out}} - A$
其中， ${D_{out}}$ 是出度矩阵。
注：使用出度矩阵而不是入度矩阵是因为拉普拉斯矩阵的设计主要是为了反映节点之间的连接性，特别是节点的“输出”行为。在有向图中，出度矩阵描述了每个节点的出边数量，而拉普拉斯矩阵的作用是通过节点的出度来衡量其对其他节点的影响。对于有向图，出度矩阵比入度矩阵更常用于拉普拉斯矩阵的定义，因为它体现了每个节点“发出的连接”。

强连通性的作用：

拉普拉斯矩阵的零特征值的个数与图的连通性密切相关：
- 如果图是强连通的，则拉普拉斯矩阵的零特征值的个数为 1。
- 如果图是不连通的，则拉普拉斯矩阵的零特征值的个数等于图的连通分量的个数。
这种特征值的分析能够帮助判断图的连通性及其结构。

【例】图的邻接矩阵：
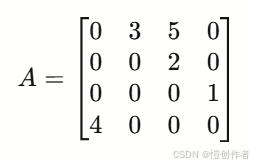
在这里插入图片描述
出度矩阵：

所以，计算拉普拉斯矩阵：

3、广义拉普拉斯矩阵（Generalized Laplacian Matrix）

广义拉普拉斯矩阵是拉普拉斯矩阵的一种推广，适用于加权有向图。在广义拉普拉斯矩阵中，度矩阵的元素不仅是节点的度数，还涉及节点的权重。它涉及到权重矩阵，而不仅仅是度矩阵。

定义：广义拉普拉斯矩阵的定义为：
标准广义拉普拉斯矩阵（基于入度矩阵） ${L_g} = D_{in}^{ - 1}A$
这种形式强调了节点的接收度，通常用于处理传播过程或图中的影响力。
标准广义拉普拉斯矩阵（基于入度矩阵） ${L_g} = D_{in}^{ - \frac{1}{2}}AD_{out}^{ - \frac{1}{2}}$
注：广义拉普拉斯矩阵常用于谱图理论中，它通过归一化邻接矩阵来控制不同节点的度数差异，使得图的结构能够更加平滑地体现出来。对于有向图的广义拉普拉斯矩阵，使用入度矩阵而不是出度矩阵是为了突出节点的“接收”行为。尤其在处理有向图时，入度矩阵反映了节点的接收强度，进而影响节点之间的相互关系和传播效果。
这种形式在对称化过程中兼顾了入度和出度，常用于一些平衡传播或对称化的场景。

连通性的作用：

通过广义拉普拉斯矩阵的特征值分解，可以分析图的连通性。特别是，图的第二小特征值（谱间隙）与图的连通性密切相关：
如果第二小特征值较大，图是连通的。
如果第二小特征值接近零，图可能是分离的，即存在多个连通分量。

【例】图的邻接矩阵：
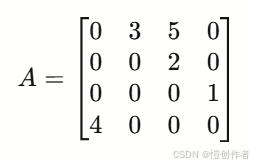
在这里插入图片描述
入度矩阵：

所以，计算广义拉普拉斯矩阵：

4、不可约拉普拉斯矩阵（Irreducible Laplacian Matrix）

不可约矩阵的定义
一个矩阵被称为不可约（Irreducible），如果它的任何部分子矩阵都不可通过重新排列矩阵的行和列来使其变成块对角形结构。换句话说，一个矩阵是不可约的，表示其所描述的系统无法拆分为多个独立的部分。

对于一个拉普拉斯矩阵而言，如果矩阵是不可约的，那么对应的图也是连通的，即图中不存在任何可以完全隔离的子图。

对于无向图，拉普拉斯矩阵是不可约的，意味着图是连通的（图中任意两个节点之间都可以通过路径连接）。
对于有向图，拉普拉斯矩阵是不可约的，意味着图是强连通的（每对节点之间都有路径相互可达）。

不可约拉普拉斯矩阵的性质

连通性与不可约性：如果一个图的拉普拉斯矩阵是不可约的，那么图是连通的（无向图）或强连通的（有向图）。反之，如果图是不可分的（即存在不连通的子图），那么其拉普拉斯矩阵是可约的。
特征值分析：
- 对于一个连通的无向图，其拉普拉斯矩阵的零特征值的代数重数为 1。
- 对于有向图，如果图是强连通的，则拉普拉斯矩阵的零特征值的代数重数也为 1。
- 拉普拉斯矩阵的其余特征值都是正的（在标准的加权图中，拉普拉斯矩阵的特征值是实数且非负的）。
谱间隙（Spectral Gap）：拉普拉斯矩阵的第二小特征值（即谱间隙）在图的连通性分析中有着重要作用。对于一个不可约的拉普拉斯矩阵，第二小特征值越大，图的连通性越强。特别是：
- 对于无向图，第二小特征值越大，图的连通性越强，意味着节点之间的信息传播会更快。
- 对于有向图，强连通的程度可以通过谱间隙来反映。

【例】图的邻接矩阵：
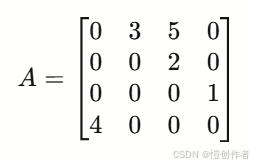
在这里插入图片描述
可以看出：

从A到B、C有路径（通过权重3和5），
从B到C有路径（权重2），
从C到D有路径（权重1），
从D到A有路径（权重4）。
这个图是强连通的，因为每个节点都可以通过某些路径到达其他节点。因此，图的拉普拉斯矩阵就是不可约的。
由于图是强连通的，不可约拉普拉斯矩阵就是标准的拉普拉斯矩阵。
即，不可约拉普拉斯矩阵与之前的拉普拉斯矩阵相同：

5、冗余矩阵（Redundancy Matrix）

冗余矩阵是基于图的邻接矩阵和度矩阵的组合，通常用于衡量图中节点之间的冗余路径数量。

通过冗余矩阵，可以评估一个图的连通性是否因某些节点或边的缺失而受到影响。

连通性的作用：

高冗余矩阵的值表明图的节点之间有多个路径连接，从而增强了图的连通性。

6、传递矩阵（Propagation Matrix）

传递矩阵表示图中信息传播的过程，通常指的是邻接矩阵的高次幂。这个矩阵描述了从某一节点出发，经过若干步可以到达其他节点的信息。

定义：传递矩阵 ${P_k}$ 为邻接矩阵的第 𝑘次幂：
${P_k} = {A^k}$
其中 ${P_k}[i][j]$ 表示从节点 𝑖到节点 𝑗经过 𝑘步路径的数量。

连通性的作用：

如果图是连通的，那么在某个合适的 𝑘值下，所有的节点都能通过 𝑘 步路径相互连接，传递矩阵中的每个元素都大于零。
如果图是非连通的，传递矩阵将显示出某些节点无法通过任何路径到达其他节点。
在强连通图中，存在一个 k，使得 ${A^k}$ 的所有元素都大于零。如果某些元素 ${P_k}[i][j] = 0$ ，说明节点 𝑖和节点 j之间没有路径，那么图不是强连通的。

7、节点相似度矩阵（Node Similarity Matrix）

节点相似度矩阵用于衡量节点之间的相似度，基于图的结构信息来反映节点的连通性强弱。

定义：节点相似度矩阵 S 通常通过计算节点间的共同邻居数量或者通过图卷积方法得出。

连通性的作用：

如果图中节点之间的相似度较高，表明它们在结构上彼此靠近，图的连通性较强。
通过相似度矩阵，可以评估图中各节点的连通性程度。

8、特征向量中心性（Eigenvector Centrality）

特征向量中心性通过图的邻接矩阵的特征值分解来衡量图中节点的重要性，节点的重要性与其邻居的中心性相关。

定义：特征向量中心性是邻接矩阵的最大特征值对应的特征向量分量。

连通性的作用：

节点的特征向量中心性高，意味着该节点在图中的连通性较强，能在图中传播信息或影响力。
如果整个图的特征向量中心性分布均匀，表明图是连通的且结构较为平衡。

9、谱半径（Spectral Radius）

谱半径是指图的邻接矩阵的特征值中的最大模。它与图的连通性以及图的扩展性（如图的稳定性、传播速率等）有关系。

定义：图的邻接矩阵 A 的谱半径为：
$\rho (A) = \max \left| {{\lambda _i}} \right|$
其中， ${{\lambda _i}}$ 是邻接矩阵 A 的特征值。

连通性的作用：

谷歌的 PageRank 算法和一些网络稳定性分析涉及到谱半径的计算。谱半径较大的图通常是连通的，因为更大的谱半径表明图的传递性较强，节点之间的影响力较大。

10、强连通分量矩阵（Strongly Connected Components Matrix）

强连通分量（SCC）是图中一个重要的子图，其中每两个节点都能互相到达。在有向图中，可以使用矩阵来表示强连通分量。

定义：强连通分量矩阵可以通过计算邻接矩阵的传递闭包得到。图的强连通分量矩阵 SCC 是一个 $\left| V \right| \times \left| V \right|$ 的矩阵，表示图中不同节点间是否属于同一个强连通分量。具体地：

强连通性的作用：
如果图是强连通的，那么图的强连通分量矩阵将是全1矩阵，即 SCC[i][j]=1 对所有 i,j 都成立。