

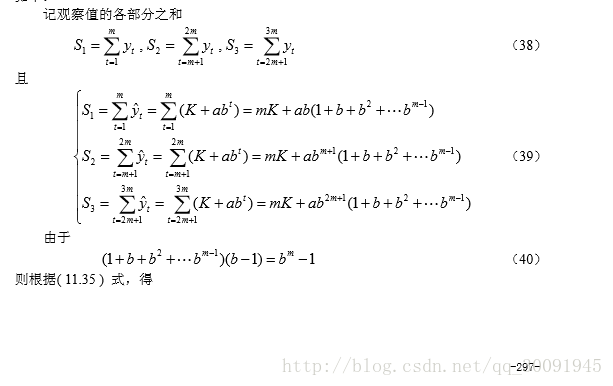

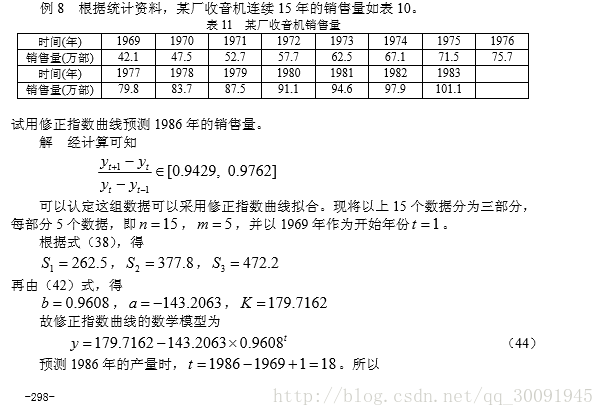
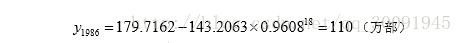
修正指数曲线法Python代码如下:
# -*- coding: utf-8 -*-
"""
Created on Sun Jan 15 15:36:15 2017
@author: DaiPuWei
"""
'''
时间序列修正指数曲线法,以收音机销售量为例
'''
import pandas as pd
import numpy as np
import math
def Check_Data(data):
'''
检查数据增长率函数,即检查增长率是否稳定在某一常数
data是数据样本
'''
error = []
flag = False
for i in range(1,len(data)-1):
err1 = data[i+1] - data[i]
err2 = data[i] - data[i-1]
error.append(err1/err2)
tmp = np.array(error)
_range = sum(tmp) / len(tmp)
if all(tmp>_range-0.2) and all(tmp<_range+0.2):
flag = True
return flag
def subarrsum(data,start,end):
'''
数组切片求和
'''
tmp = []
for i in range(start,end):
tmp.append(data[i])
return sum(tmp)
def Index_Curve_Model(data,year,T):
"""
修正指数曲线方法
模型为: Y(t) = K + a * b^(t-t0+1)
data为数据集
T为预测年份
"""
forecast = 0
#增长率若稳定在某一常数则进行模型求解
if Check_Data(data) == True:
#将数据分成3份
len1 = (int)(len(data) / 3)
len2 = len(data) - len1
len3 = len(data)
#各份数据的总和
tmp = []
for i in range(len(data)):
tmp.append(data[i])
sum1 = subarrsum(data,0,len1)
sum2 = subarrsum(data,len1,len2)
sum3 = subarrsum(data,len2,len3)
#各个参数值的求解
b = math.pow((sum3-sum2)/(sum2-sum1),1.0/len1)
a = (sum2-sum1) * (b-1) / (b * (math.pow(b,len1)-1) * (math.pow(b,len1)-1))
K = (sum1 - a*b*(math.pow(b,len1)-1)/(b-1)) / len1
if a > 0:
print('修正指数曲线模型: Y(t)=',K,'+',a,'*',b,'^(T-',year[0],')')
elif a == 0:
print('修正指数曲线模型: Y(t)=',K)
elif a < 0:
print('修正指数曲线模型: Y(t)=',K,a,'*',b,'^(',T,'-',year[0],'+1)')
forecast = K + a * math.pow(b,T-year[0]+1)
else:
print("数据不真实,重新输入数据!")
return forecast
def run_main():
'''
这是主函数
'''
#读取数据集
sample = pd.read_excel('E:\\Program Files (x86)\\大学数学\\算法大全pdf\\第24章 时间序列模型\\收音机销售量.xlsx')
data = sample[sample.columns[1]]
year = sample[sample.columns[0]]
#模型预测
T = 1986
forecast = Index_Curve_Model(data,year,T)
print(T,'年的收音机销售额预测值为:',forecast)
if __name__ == '__main__':
run_main()

Compertz曲线法Python代码如下:
# -*- coding: utf-8 -*-
"""
Created on Sun Jan 15 21:54:47 2017
@author: DaiPuWei
"""
'''
时间序列Compertz曲线法,以收音机销售量为例
'''
import pandas as pd
import numpy as np
import math
def Check_Data(data):
'''
检查数据增长率函数,即检查增长率是否稳定在某一常数
data是数据样本
'''
error = []
flag = False
for i in range(1,len(data)-1):
err1 = data[i+1] - data[i]
err2 = data[i] - data[i-1]
error.append(err1/err2)
tmp = np.array(error)
_range = sum(tmp) / len(tmp)
if all(tmp>_range-0.2) and all(tmp<_range+0.2):
flag = True
return flag
def subarrsum(data,start,end):
'''
数组切片求和
'''
tmp = []
for i in range(start,end):
tmp.append(data[i])
return sum(tmp)
def Compertz_Model(data,year,T):
"""
修正指数曲线方法
模型为: Y(t) = e^(K + a * b^(t-t0+1))
data为数据集
T为预测年份
"""
forecast = 0
#增长率若稳定在某一常数则进行模型求解
if Check_Data(data) == True:
#将数据分成3份
len1 = (int)(len(data) / 3)
len2 = len(data) - len1
len3 = len(data)
#各份数据的总和
tmp = []
for i in range(len(data)):
tmp.append(data[i])
sum1 = subarrsum(data,0,len1)
sum2 = subarrsum(data,len1,len2)
sum3 = subarrsum(data,len2,len3)
#各个参数值的求解
b = math.pow((sum3-sum2)/(sum2-sum1),1.0/len1)
a = (sum2-sum1) * (b-1) / (b * (math.pow(b,len1)-1) * (math.pow(b,len1)-1))
K = (sum1 - a*b*(math.pow(b,len1)-1)/(b-1)) / len1
if a > 0:
print('Compertz曲线模型: Y(t)=',K,'*',a,'^(',b,'^(T-',year[0],'+1))')
elif a == 0:
print('Compertz曲线模型: Y(t)=',K)
elif a < 0:
print('Compertz曲线模型: Y(t)=',K,'*(',a,')^(',b,'^(T','-',year[0],'+1))')
tmp = math.pow(b,T-year[0]+1)
forecast = K + a*tmp
forecast = math.exp(forecast)
else:
print("数据不真实,重新输入数据!")
return forecast
def run_main():
'''
这是主函数
'''
#读取数据集
sample = pd.read_excel('E:\\Program Files (x86)\\大学数学\\算法大全pdf\\第24章 时间序列模型\\收音机销售量.xlsx')
data = sample[sample.columns[1]]
_data = []
for i in range(len(data)):
_data.append(math.log(data[i]))
year = sample[sample.columns[0]]
#模型预测
T = 1986
forecast = Compertz_Curve_Model(_data,year,T)
print(T,'年的收音机销售额预测值为:',forecast)
if __name__ == '__main__':
run_main()



Logistic曲线(生长曲线)法Python代码如下:
# -*- coding: utf-8 -*-
"""
Created on Sun Jan 15 22:07:39 2017
@author: DaiPuWei
"""
'''
时间序列Compertz曲线法,以收音机销售量为例
'''
import pandas as pd
import numpy as np
import math
def Check_Data(data):
'''
检查数据增长率函数,即检查增长率是否稳定在某一常数
data是数据样本
'''
error = []
flag = False
for i in range(1,len(data)-1):
err1 = data[i+1] - data[i]
err2 = data[i] - data[i-1]
error.append(err1/err2)
tmp = np.array(error)
_range = sum(tmp) / len(tmp)
if all(tmp>_range-0.2) and all(tmp<_range+0.2):
flag = True
return flag
def subarrsum(data,start,end):
'''
数组切片求和
'''
tmp = []
for i in range(start,end):
tmp.append(data[i])
return sum(tmp)
def Logistic_Model(data,year,T):
"""
修正指数曲线方法
模型为: Y(t) = 1/(K + a * b^(t-t0))
data为数据集
T为预测年份
"""
forecast = 0
#增长率若稳定在某一常数则进行模型求解
if Check_Data(data) == True:
#将数据分成3份
len1 = (int)(len(data) / 3)
len2 = len(data) - len1
len3 = len(data)
#各份数据的总和
tmp = []
for i in range(len(data)):
tmp.append(data[i])
sum1 = subarrsum(data,0,len1)
sum2 = subarrsum(data,len1,len2)
sum3 = subarrsum(data,len2,len3)
#各个参数值的求解
b = math.pow((sum3-sum2)/(sum2-sum1),1.0/len1)
a = (sum2-sum1) * (b-1) / (b * (math.pow(b,len1)-1) * (math.pow(b,len1)-1))
K = (sum1 - a*b*(math.pow(b,len1)-1)/(b-1)) / len1
if a > 0:
print('Logistic曲线模型: Y(t)=1/(',K,'+',a,'*',b,'^(T-',year[0],'+1))')
elif a == 0:
print('Logistic曲线模型: Y(t)=',K)
elif a < 0:
print('Logistic曲线模型: Y(t)=1/(',K,'+',a,'*',b,'^(T','-',year[0],'+1))')
tmp = math.pow(b,T-year[0]+1)
forecast = K + a*tmp
forecast = 1.0 / forecast
else:
print("数据不真实,重新输入数据!")
return forecast
def run_main():
'''
这是主函数
'''
#读取数据集
sample = pd.read_excel('E:\\Program Files (x86)\\大学数学\\算法大全pdf\\第24章 时间序列模型\\收音机销售量.xlsx')
data = sample[sample.columns[1]]
_data = []
for i in range(len(data)):
_data.append(1.0/data[i])
year = sample[sample.columns[0]]
#模型预测
T = 1986
forecast = Logistic_Model(_data,year,T)
print(T,'年的收音机销售额预测值为:',forecast)
if __name__ == '__main__':
run_main()
(时间序列模型中的ARMA模型由于原理对我来说理解有些困难,加之最近的北美数学建模大赛即将开始,自己为了顾全大局,多看掌握几个重要模型,所以ARMA模型的Python代码暂时不更新,等比赛过后有时间再更新!!!!)























 3717
3717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










