【数学模拟卷总结】2022李林四套卷数学二第四套

本文链接：https://blog.csdn.net/qq_30204431/article/details/127612944

写这个系列是为了逼自己总结
这套题写的并不好，分数较低，150党和什么秒了党抓紧退散

题目复盘

把 $l n$ 拆成两项差用泰勒展开就算出来了
斜渐近线定义，原极限改写为 $A=\lim_{x \to +\infty }\limits \frac{1+x+f(x)}{e^{-x}}$ ，然后直接改写成定义式 $\lim_{x \to +\infty} \limits1+x+f(x)=0$ 即 $f (x) = - x - 1 + o (1)$ ，所以斜渐近线就是 $y = - x - 1$
***这题我算错了，其实就是二阶混合偏导数相等定参数，结果算错了，早上状态不佳，没看到下面的 $x^2+y^2$ 是二次项，这题计算量有点离谱，作为选择题搞人心态，算了半小时还是错，重新复盘如下：

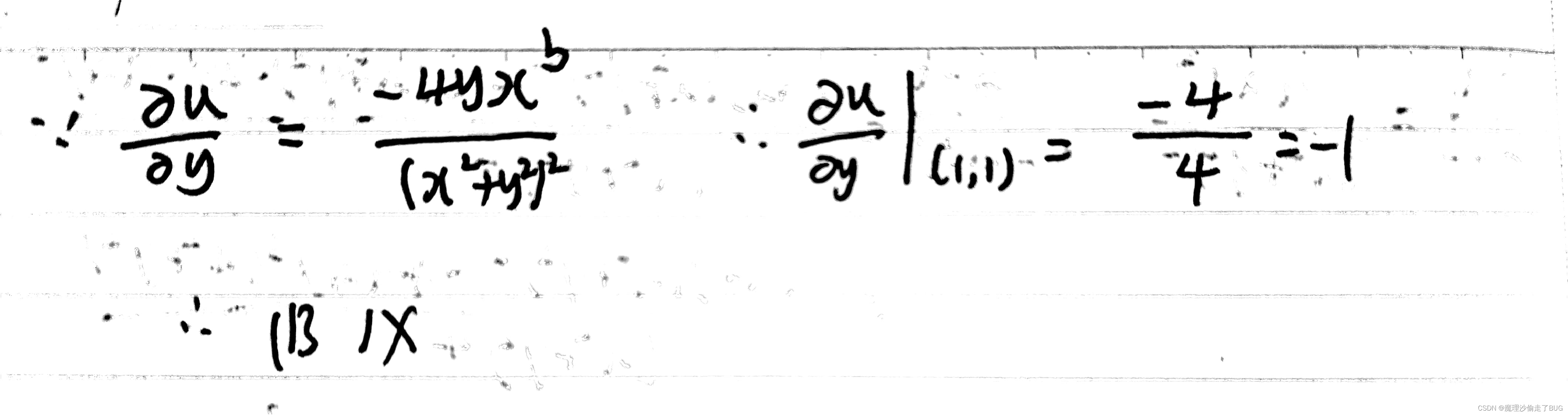
到了这里只定出了参数b，还要想尽办法定参数a，因为最主要的就是求a

这题目的计算量是真的大，要算吐了，选择题出这种题……不合理吧……
***这题我做错了，这是一类积分比大小的问题，它本质上就是不等式问题，只不过会加了点积分的技巧，我遇到这种问题就头疼，可能和高中的时候我们没学不等式那本选修有关吧（我们选修学的是极坐标和参数方程，没学不等式，本科一年级我恶补了一下不等式），复盘完成后我抓紧再找几个积分比大小的题目练一练，这题目用到了如下结论：
（1） $\int_{0}^{\pi}xf(sinx)dx=\frac{\pi}{2}\int_{0}^{\pi} f(sinx)dx$ ；
（2）积分中需要将 $s in x$ 和 $cos x$ 互换，且积分区间是 $(0,k\pi)$ ，则令 $t=\frac{k\pi}{2}-x$ 换元即可。
重新复盘如下：
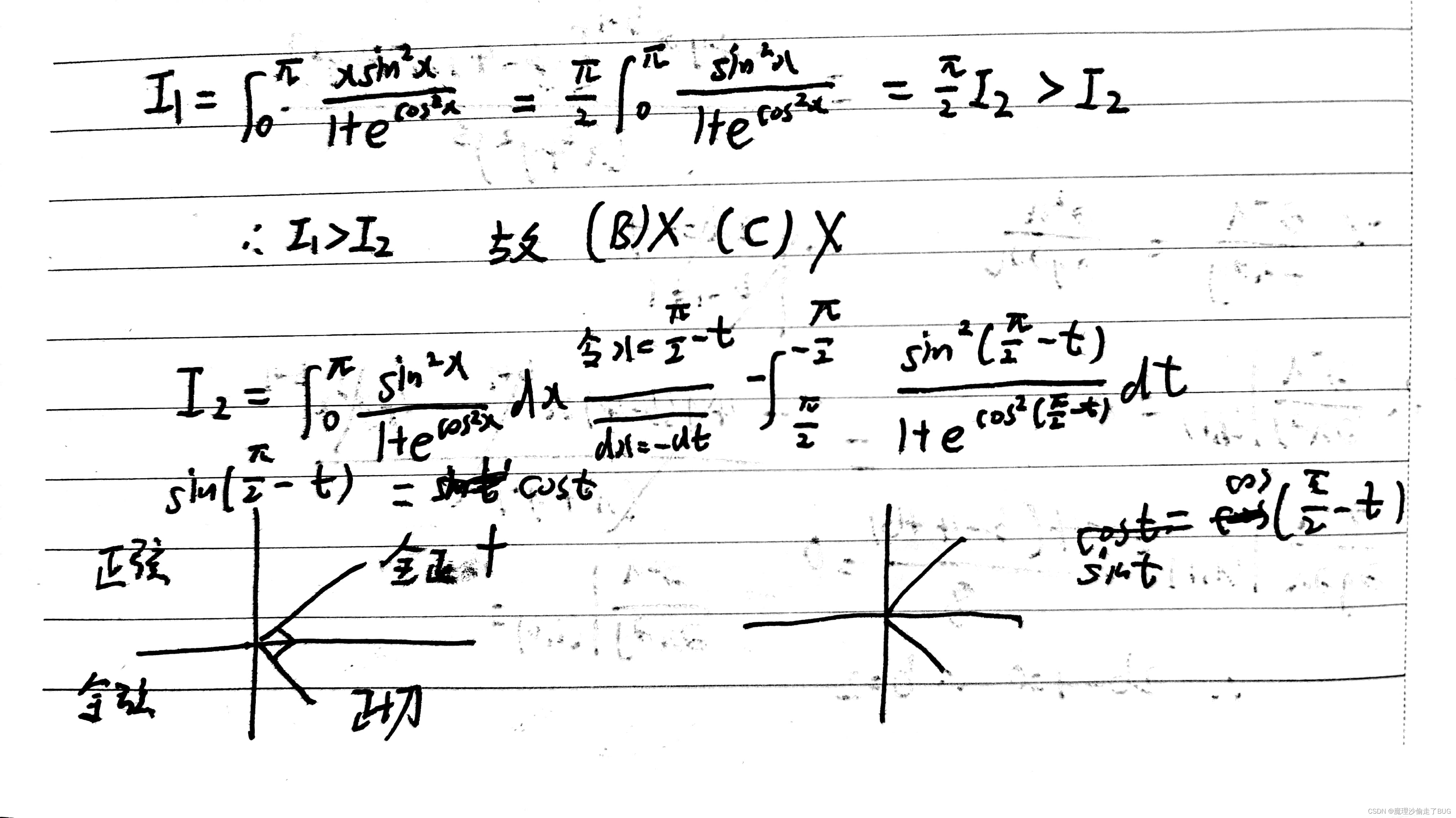
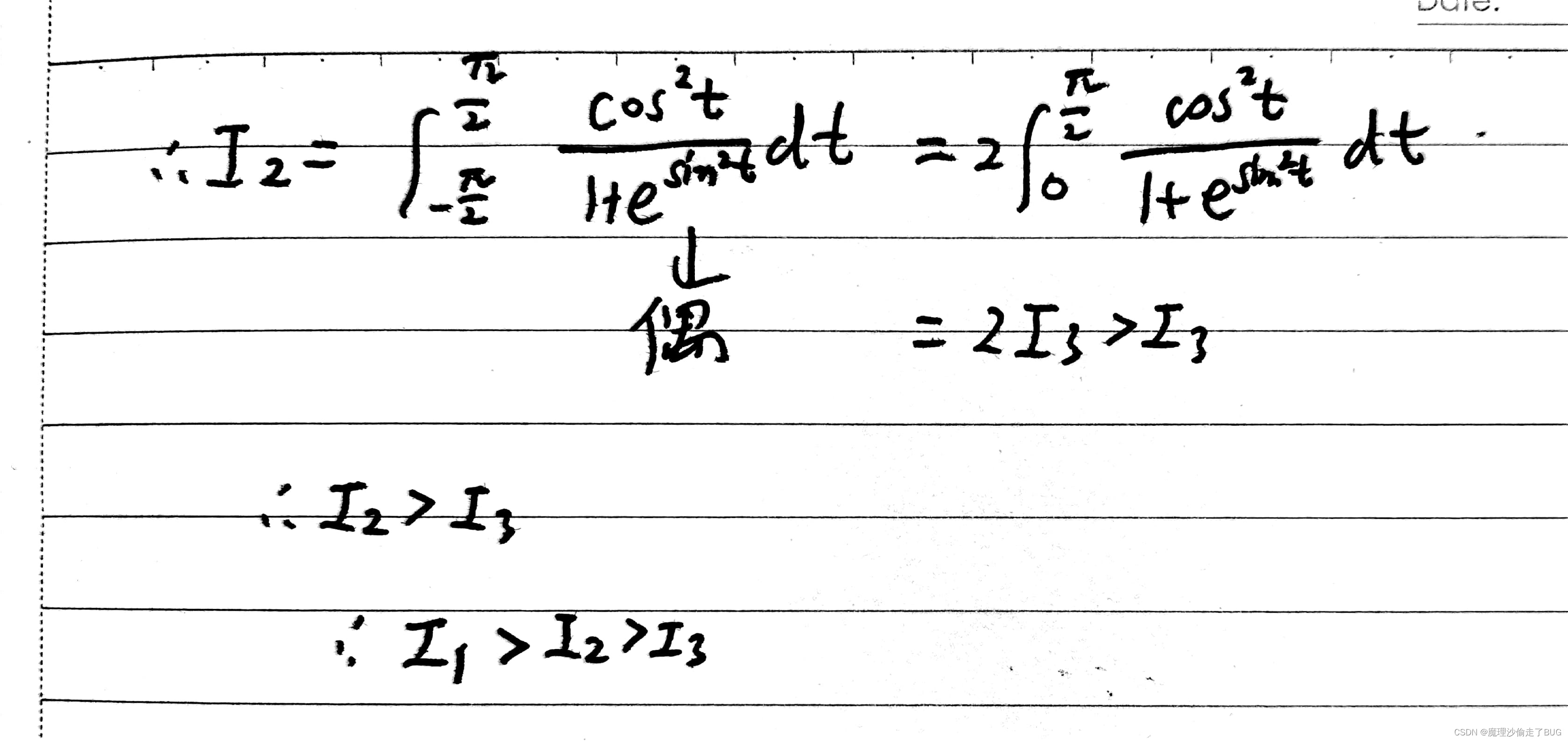【注】遇到更棘手的带有三角函数的积分可以考虑区间再现公式。
***这题我做错了，这题不是常见的 $(0, 1)$ 区间的定积分定义，所以我就没有想到方法，需要从黎曼积分定义 $\int_{a}^{b} f(x) \mathrm{d} x=\lim _{n \rightarrow \infty}\limits \frac{b-a}{n}\sum_{i=1}^{n}\limits f\left(a+\frac{b-a}{n} i\right)$ 这个角度做推理，再结合极坐标图形面积公式，重新复盘如下：
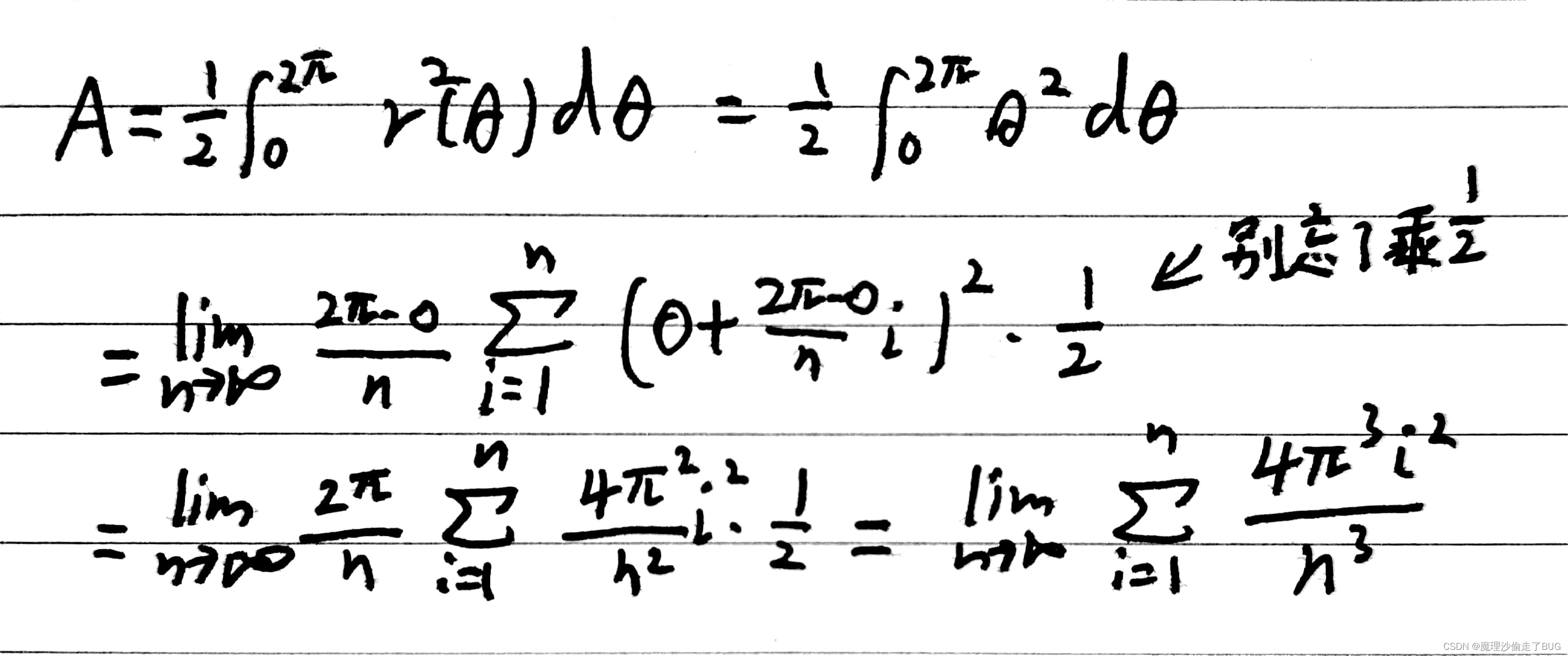
求一下导数，发现驻点是极小值点，大概画一下图形就发现区间端点可能取到最值，比一下区间端点就做出来了。
***这题我算错了，这题是魔改的历年真题，具体哪一年我忘了，但是我做的时候分母少写了平方，马虎了，重新复盘如下：
不能线性表示就是非齐次方程组无解也就是系数矩阵的秩不等于增广矩阵的秩，做一下初等变换就定出了参数，注意别算错就行，我最讨厌算初等变换，因为好多数字一起算，很容易出错，尤其是求逆矩阵的初等变换更恶心。
**本题知道下面这个结论就做出来了：
齐次方程组同解的结论

非齐次方程组把上面的矩阵换成增广矩阵是一样的

对于C选项，由矩阵等价只能推出 $r(\boldsymbol A)=r(\boldsymbol B)$ ，矩阵等价的定义如下：

向量组等价只能推矩阵等价，但是矩阵等价不一定向量组等价。矩阵等价是经过有限次初等变换，不一定只是初等行变换，还可能是初等列变换，而且矩阵等价只能说明 $r(\boldsymbol A)=r(\boldsymbol B)$ ，不能说明 $r(\boldsymbol A)=r(\boldsymbol B)=r\left(\begin{array}{l} \boldsymbol A \\ \boldsymbol B \end{array}\right)$ ，所以C选项错误。
D选项没有此结论，可以举几个反例。

正交变换化成的标准型的系数必为特征值，这样 $\boldsymbol A$ 行列式就求出来了，再根据 $\boldsymbol A\boldsymbol A^{*}=\boldsymbol A^{*}\boldsymbol A=|\boldsymbol A|\boldsymbol E$ 就推出另外一个二次型矩阵是 $-\boldsymbol E$ ，这样它必相似于对角矩阵它自己，它的特征值三个都是 $- 1$ ，所以选规范型选三个项都是负数系数的即可。
***这题我马虎了，大早上起来做核酸太困了，题目求曲率半径，我求成了曲率，就差个倒数，重新复盘如下：
求一下二阶导数定拐点（二阶导数变号点），求出两个拐点分别求一下其法线过原点的情况，因为原曲线是个四次的曲线，两个法线定出来的 $k$ 是一致的。
**取成对数求极限好算，这题我没在考试的时候严格做，随便用了一下夹逼准则，现在严格做如下：
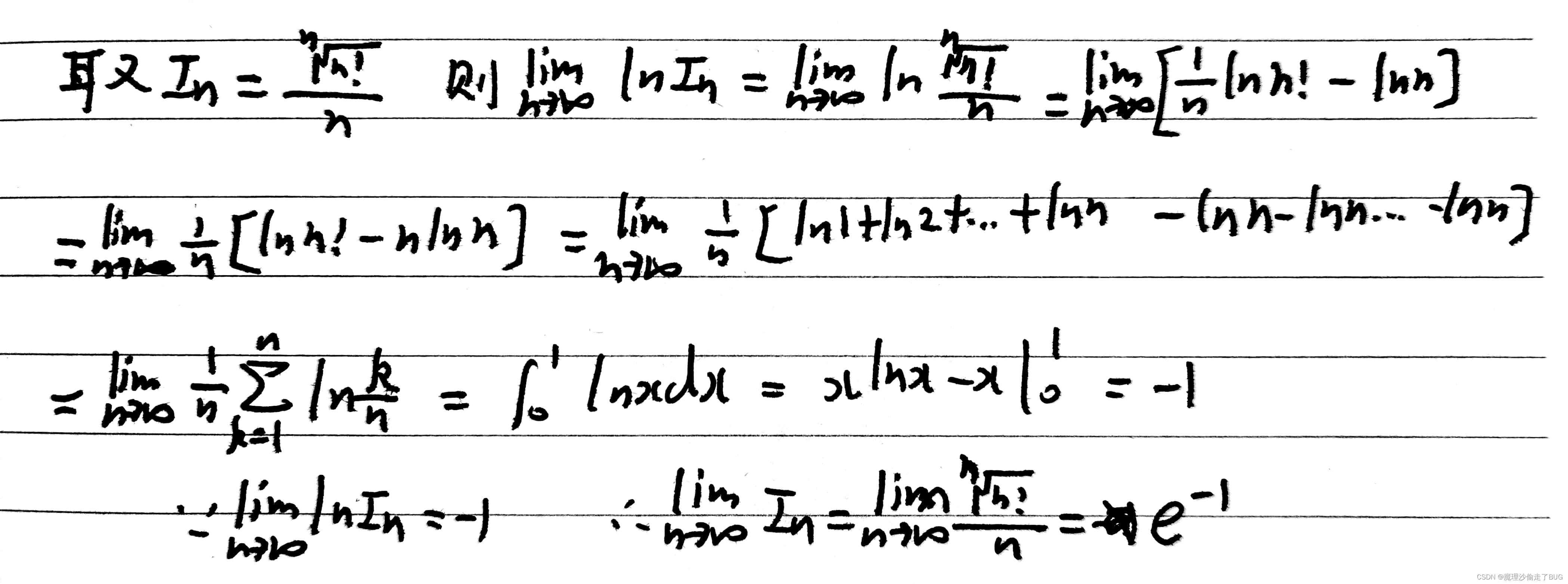
***这题我做错了，这题其实就是2019年数学二魔改，本题坑人就坑在 $\sqrt{sinx}$ 的定义域是 $\ge 0$ ，这样就只能求 $s in x$ 大于0时的区间的旋转体体积，按答案来要分区间求和，那就是无穷级数了（数二经常打擦边球考无穷级数），这种题出成填空题真是……恶心人，重新复盘如下：
极坐标化成直角坐标好算。
余子式加和结果替换行列式第一行。
***这题我做错了，我知道要凑导数定义，但是没想明白怎么凑，看了答案才明白，重新复盘如下：
把二重积分令成A，回代再求二重积分，用一下奇偶性和对称性去掉一些复杂项，剩下简单的就求出来了，然后就求出二元函数表达式。
**把 $y_{2}$ 带入原微分方程中，然后解关于 $u (x)$ 的微分方程，然后 $y_{1}$ 和 $y_{2}$ 线性无关就是原方程的通解，我不知道通解要线性无关，就随便蒙对了答案，这个要注意。
***这题第二问我没思路，第一问就是数学归纳法找规律，第二问重新复盘如下：

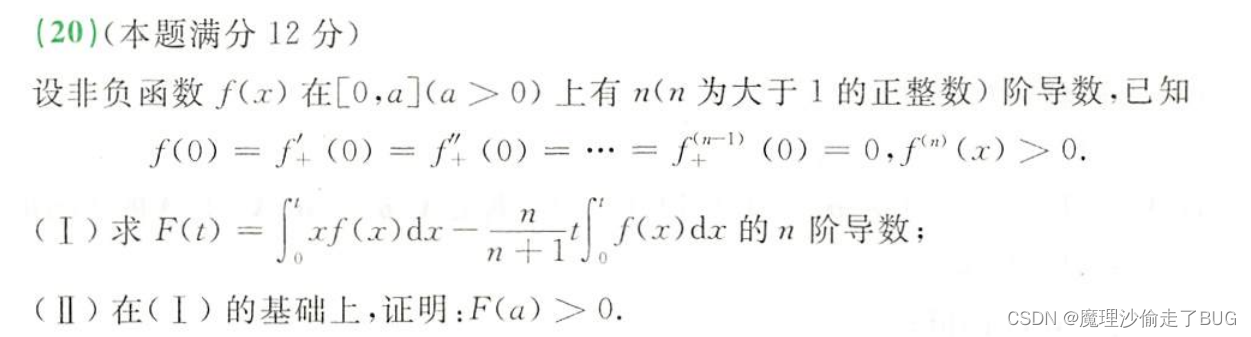
以后见到 $f (x)$ 后面缺东西构造拉格朗日中值定理的形式，立刻找题目添加看一看有没有 $f(x_{0})=0$ ，如果有的话，就直接构造 $f(x)-f(x_{0})$ 的拉格朗日中值定理的式子。
**第一问构造函数从零点定理和单调性两个角度说明零点唯一，第二问有点意思，没法证明到底是单调增还是单调减少，我是用 $F (x)$ 单调递增证明数列是单调的，但是这个不严谨，看看答案的证法。