【数学模拟卷总结】2023李林六套卷数学二第二套

写这个系列是为了逼自己总结，这套卷强度上来了，分数不理想，所以要仔细复盘，选择填空了用了1.5小时，解答题17题我最开始没算出来，后来去做线性代数解答题，再后来返回来做解答题，时间紧迫，二重积分的题目都算错了。

题目复盘

1. 题目没说$f(x)$在0点是否连续，这个极限式只能说明$f(x)$在0的去心邻域内有定义，所以由这个极限式只能说明$\underset{x\to 0}{\lim }f(x)=0$.
2. **这个题的（1）和（2）我和答案举的反例一样，然后用排除法就做出来了，但是复盘要把（3）和（4）搞明白，首先由于$x_n\in [-1,1]$，则数列$x_n$有界，（3）中说 { x n } \{x_{n}\} {xn​}收敛，翻了翻同济教材有这样一条定理：
   
   首先 { x n } \{x_{n}\} {xn​}收敛，则$f(x_n)=arcsin(x_n)$收敛，（4）中，$x_n\in [-1,1]$，所以$x_n$有界，而且 { x n } \{x_{n}\} {xn​}单调，由单调有界准则可知，则$\underset{n\to \infty }{\lim }{x}_n=A$存在，且$-1\le A\le 1$（有界限定的），所以$arcsin(x_n)$一定收敛，（看$arcsinx$图像可知，其定义域就是$(-1,1)$），$arcsinx$图像如下所示：
   
3. 积分拆开以后用分部积分即可推出，这个是某年真题魔改的。
4. **这题我和答案的做法不一样，先看我的做法：
   我有两种思路，思路1是考场上想到的，思路2是复盘时想到的：
   答案是按泰勒的思路做下去，也可以
   
   其实看到二阶导数不等式想泰勒最稳妥，要给自己不断灌输这种做题的思维定式，还有看到$\frac{f^{\prime }(x)}{f(x)}$这种形式一定要想到构造辅助函数$H(x)=ln(f(x))$，要形成思维定式。
5. 反常积分，先看瑕点$x\to 1^{+}$，此时$lnx=ln(1+x-1)\sim x-1$，原反常积分的被积函数等价于$\frac{1}{(x-1{)}^q}$，根据P积分，$q<1$收敛，瑕点正无穷需要用到下面几个结论：
   $$\begin{gathered} \text{ 对 }\forall \alpha ,\beta >0,\text{ 其中 }a>1: \\ \{\begin{array}{l}{\int }_a^{+\infty }\frac{{\ln }^{\beta }x}{x^{\alpha }}dx,\alpha >1\text{, 收敛 }\\ {\int }_a^{+\infty }\frac{1}{x^{\alpha }{\ln }^{\beta }x}dx,\alpha >1\text{, 收敛 }\\ {\int }_a^{+\infty }\frac{1}{x^{\alpha }{\ln }^{\beta }x}dx,\alpha <1\text{, 发散 }\\ {\int }_a^{+\infty }\frac{1}{x{\ln }^{\beta }x}dx,\beta \le 1,\text{ 发散 }\\ {\int }_a^{+\infty }\frac{1}{x{\ln }^{\beta }x}dx,\beta >1\text{, 收敛 }\end{array} \end{gathered}$$
   $$\begin{gathered} \text{ 对 }\forall \alpha ,\beta >0,\text{ 其中 }0<a<1： \\ \{\begin{array}{l}{\int }_0^a\frac{|\ln x{|}^{\beta }}{x^{\alpha }}dx,\alpha <1\text{, 收敛 }\\ {\int }_0^a\frac{1}{x^{\alpha }|\ln x{|}^{\beta }}dx,\alpha <1\text{, 收敛 }\\ {\int }_0^a\frac{1}{x^{\alpha }|\ln x{|}^{\beta }}dx,\alpha >1\text{,发散 }\\ {\int }_0^a\frac{1}{x|\ln x{|}^{\beta }}dx,\beta \ge 1\text{, 发散 }\\ {\int }_0^a\frac{1}{x|\ln x{|}^{\beta }}dx,\beta <1\text{, 收敛 }\end{array} \end{gathered}$$
   若要让题中的反常积分在无穷瑕点收敛，就要满足${\int }_a^{+\infty }\frac{1}{x^{\alpha }{\ln }^{\beta }x}dx,\alpha >1\text{, 收敛 }$或${\int }_a^{+\infty }\frac{1}{x{\ln }^{\beta }x}dx,\beta >1\text{, 收敛 }$，那么也就是说，$p>1,p任意取$或者$p=1,q>1$，但是从瑕点0处已经推知$q<1$，所以只能取前者$p>1$
6. 利用二阶混合偏导数相等的条件就算出来了，注意不算错就OK
7. 前两个选项求一下偏导数就得出，$x>0$，$|x|=x$，然后求对$x$的偏导数和$y$没关系，将$\sqrt{|y|}$视为常数即可，$x<0$，$|x|=-x$，最后会发现（A）（B）选项都错了，正负号弄反了，剩下两个选项用一下导数定义就做出来了。
8. **这题我做的时候将行列式硬着头皮算出来了，复盘的时候看了一下答案才发现，这玩意取转置就是范德蒙行列式啊，重新复盘如下：
   
   
9. ***这题我做错了，非齐次方程通解的结构是齐次的通解+一个非齐次特解，也就是说，它线性无关的解的数量是齐次通解线性无关解的数量+1个非齐次的特解的数量，我忘了加1，把这个题目标记一下：
   
   
   【注】此处用到结论$\mathbf{A}\mathbf{B}=\mathbf{O}$则$r(\mathbf{A})+r(\mathbf{B})<n$，其中$n$是$\mathbf{A}$的行数（$\mathbf{B}$的列数）。
10. 左乘$\mathbf{A}$得到一个矩阵方程，然后直接把特征值解出，再用行列式等于特征值乘积定一下每个特征值都是几重的即可算出正负惯性指数，直接选对应的规范型即可。
11. 求一下切线再带入题给点，极限就算出来了，注意要做一步恒等变形$\underset{n\to \infty }{\lim }nln\sqrt{x_n}=\underset{n\to \infty }{\lim }\frac{1}{2}nln{x}_n$
12. 对$y$的参数方程换元，按参数方程求导就做出来了
13. 求一下曲线和$x$轴结点，发现相交区间是向下的，最后做定积分的结果别忘了取负号，这题是魔改某年真题，那个真题也是一样的套路，先找$x$轴交点，然后求的是旋转体体积。
14. ***这题我没做，这题积分形式太复杂就先越过去了（换序后也不好计算），后面想了半天也没做上，重新复盘如下：
    
    
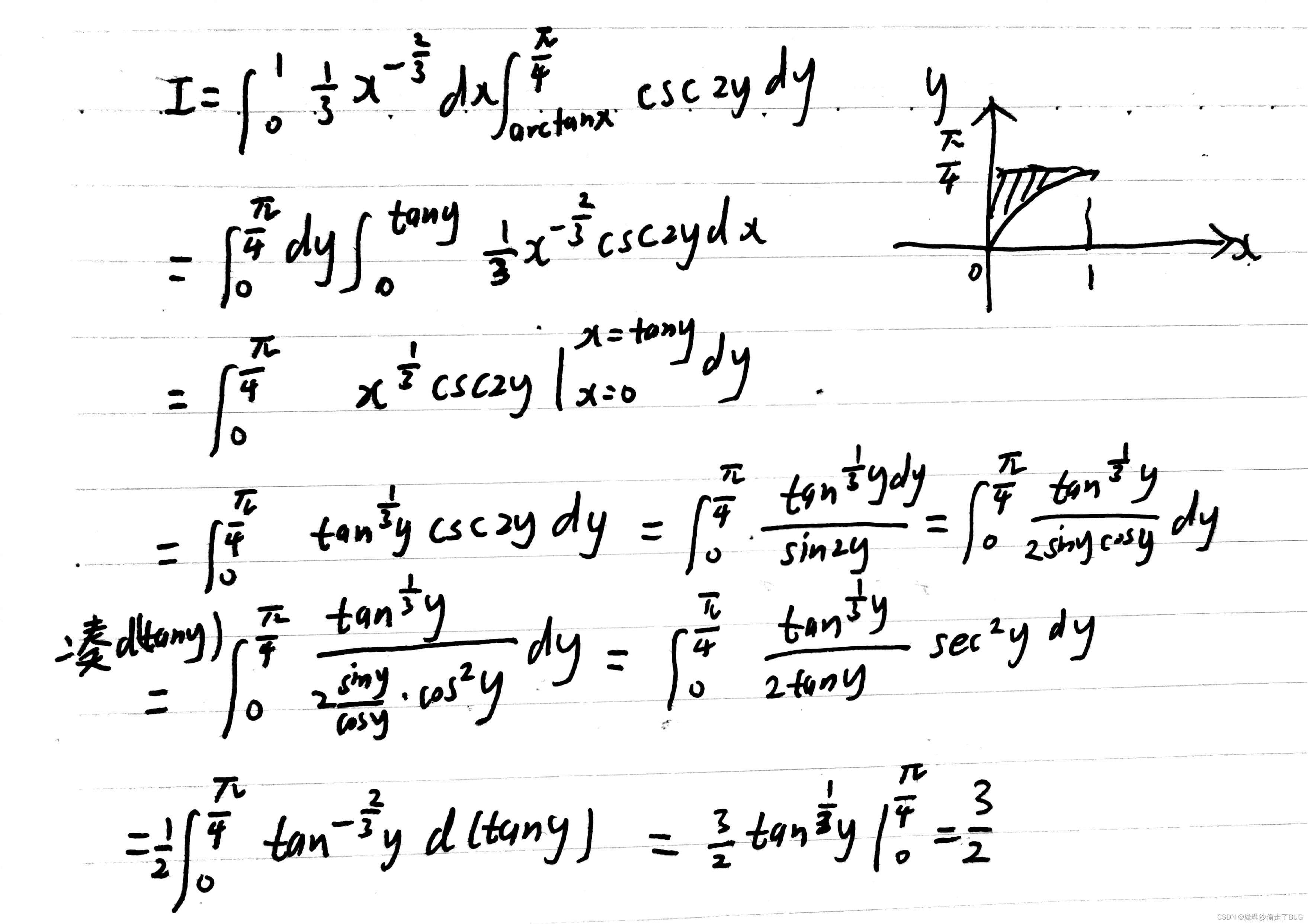
    模拟考试的时候我就卡在这个凑$d(tany)$这一块了，这个思路要记住，没见过这种题真的难想到。
15. ***这题我做错了，第一眼把题目看成求旋转体体积了，然后就算错了，以后不论多紧张都要冷静读题，本题是求旋转曲面的表面积，三个坐标系下的旋转曲面的面积公式为：
    （1）直角坐标：$S=2\pi {\int }_a^b|y(x)|\sqrt{1+{\left[y^{\prime }(x)\right]}^2}\mathrm{d}x.$
    （2）参数方程：$S=2\pi {\int }_{\alpha }^{\beta }|y(t)|\sqrt{{\left[x^{\prime }(t)\right]}^2+{\left[y^{\prime }(t)\right]}^2}\mathrm{d}t.$
    （3）极坐标：$S=2\pi {\int }_{{\theta }_1}^{{\theta }_2}|r(\theta )\sin \theta |\sqrt{[r(\theta ){]}^2+{\left[r^{\prime }(\theta )\right]}^2}d\theta$
    ，重新复盘如下：
    
    这个计算还是需要技巧性的，要不然容易卡在积分形式不知道怎么积这个问题上面，以后对于双纽线这类$r^2$定义的极坐标曲线，要注意妙用隐函数求导和分子分母同乘$r$凑$si{n}^2\theta +co{s}^2\theta =1$这样的形式化简，顺带复习一下两个双纽线：
    
    
16. 非齐次方程的特解的线性组合的系数和为0是齐次的解，系数和为1是非齐次的解，A的秩为3，Ax=b有4个未知数，所以n-r(A)=1，齐次方程有一个线性无关的解向量构成基础解系，那就用题给条件凑，直接让两个等式相减就是齐次方程的解（系数和为0），然后特解需要系数和为1，直接将第一个式子除4刚好就是系数和为1，就找到了特解，也就是答案那种形式，线性代数方程组和高等数学的微分方程都有这个特性，2010年就考到了这个性质：
    张宇的书中还有一个也是用到这个原理的题目
    
    这个题也是用解的线性组合系数和的性质来做的
17. **这题最开始我把$x=\frac{1}{t}$带入变成直角坐标发现很难算，后来用极坐标求导数，然后再求一次导数定正负就好做了，以后看到题给的信息要琢磨，既然给了极坐标，就不要去化成直角再求，求导一次看不出正负再求一次试试，不要因为这些拖慢做题速度，这个我要记住。
18. 这个题三角换元用华里士公式或者凑微分都能得到递推关系，最后求一下极限即可
19. ***这题第二问我没做上，第一问把求导路径画对了就行，看了答案，果然是去年真题魔改的，去年真题我就这个题没做上，它搞了一堆偏导数变量代换，很恶心，重新复盘如下：
    
    
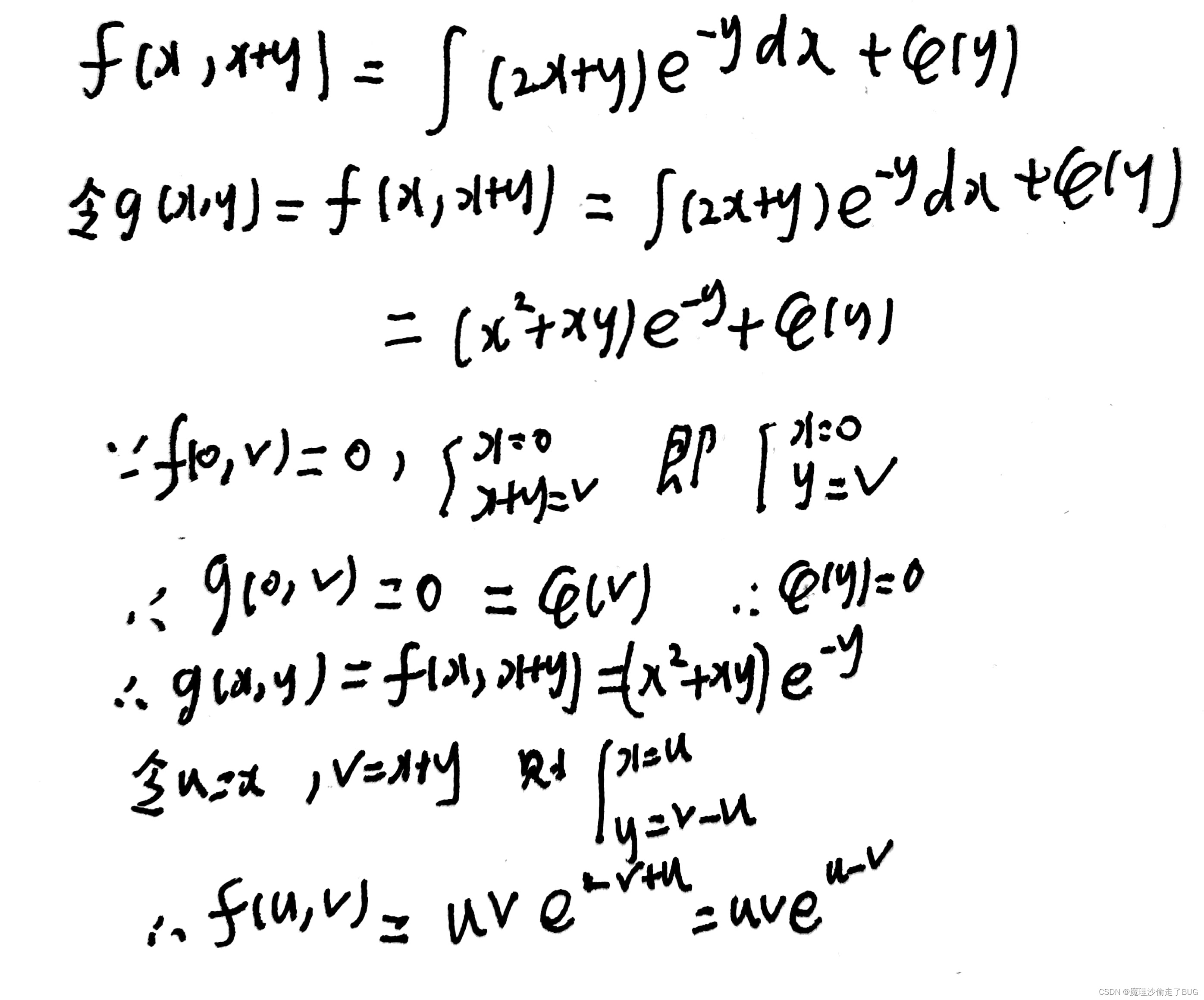
    本题魔改的是去年真题，抓紧复习一下：
    
    
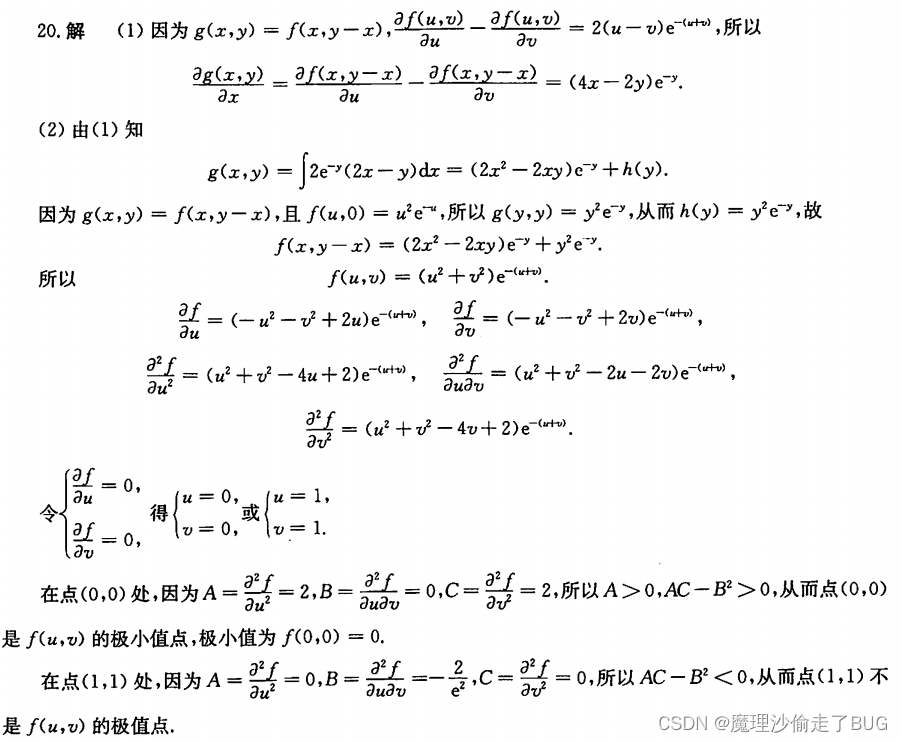
    真题这块我没掌握，算是查漏补缺了
20. ***这题我算错了，后面算的着急了，0点二阶导数求错了，题目说二阶导数连续，那就可以用洛必达，我用的是雅克比换元 ，改正如下：
    
    我觉得雅克比换元更清晰，答案那种直接换也行，每个人有不同的风格
    
21. ***这题我没做上，我没找到变化率之间的关系（忘记了牛顿第二定律，物理学得不好），重新复盘如下：
    以后记住用牛顿第二定律构造方程，速度可以用变量代换做出来，求的是dv/dt就想方设法构造就OK。
22. ***这题我第二问算错了，我和答案的思路是一样的，只是第二问算错了，第一问证明不相似，找到它的特征根对应的特征向量有不是线性无关的就行，即2重特征根只有一个线性无关的特征向量就不能相似对角化，第二问把矩阵P设出来就OK，类似某年真题的思路，那个是乘法，算错了一个方程组的解，就不重新写了，模拟考试比较着急抄错数了，这个题很新颖，记录一下：
    
    
    这个题的第二问的思路实际上是2013年真题的思路，对于这种2阶的矩阵，设出来即可：
    

总结

要加强计算能力，查漏补缺，我要加油了！