【李沐深度学习笔记】线性代数实现

课程地址和说明

线性代数实现p2
本系列文章是我学习李沐老师深度学习系列课程的学习笔记，可能会对李沐老师上课没讲到的进行补充。
这节就算之前内容的复习，后面以截图形式呈现

标量由只有一个元素的张量表示

import torch
x = torch.tensor([3.0])
y = torch.tensor([2.0])
# 加减法
print(x+y)
# 乘法
print(x * y)
# 除法
print(x / y)
# 幂运算
print(x**y)

运行结果：
tensor([5.])
tensor([6.])
tensor([1.5000])
tensor([9.])

你可以将向量视为标量值组成的列表

# 生成0-3的顺序列表，（函数是左闭右开）
x = torch.arange(4)
print(x)

运行结果：
tensor([0, 1, 2, 3])

通过张量的索引来访问任一元素

访问张量的长度

只有一个轴的张量，形状只有一个元素。

通过指定两个分量m和n来创建一个形状为m × n的矩阵

矩阵的转置

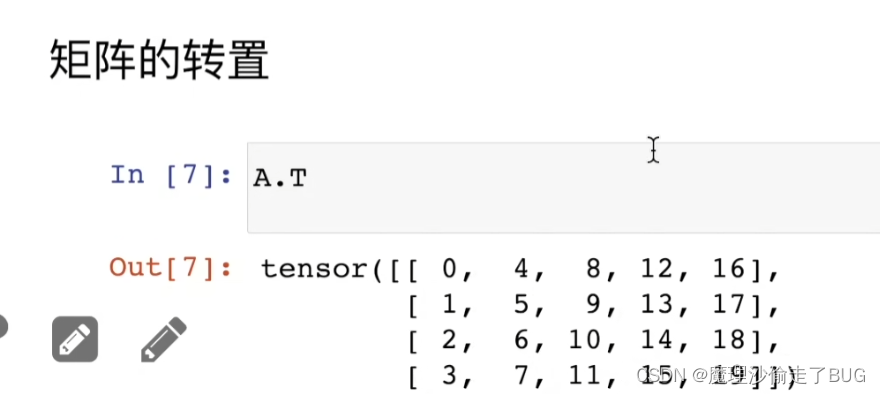
对称矩阵的转置

构造多轴的数据结构

【注】就是构建多维数组

给定具有相同形状的任何两个张量，任何按元素二元运算的结果都将是相同形状的张量

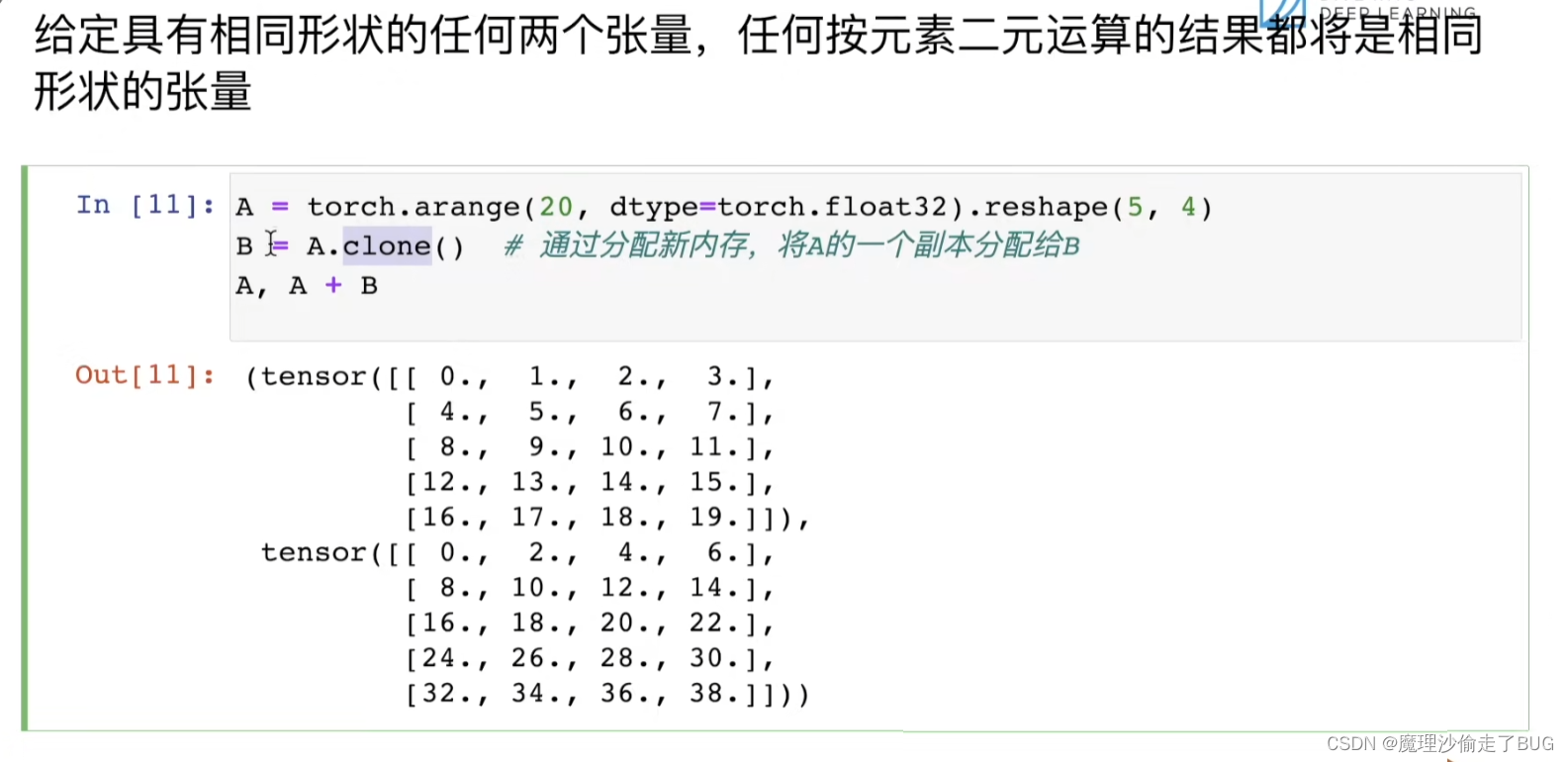
矩阵的哈达玛积

其实就是不按矩阵乘法来，按两个矩阵对应元素相乘得到个新矩阵（前提是矩阵是同形的，即两个相乘的矩阵行列数需要一致）

标量和矩阵相加是所有元素都与标量相加得到新矩阵

计算矩阵所有元素的和

表示任意形状张量的元素和

不论张量形状如何，其求所有元素和的结果永远是标量

指定求和汇总张量的轴（按不同维度求和）

【注】axis是按不同维度求和，从0开始是第1个维度。这里理解上稍微有点难度，我写了代码：

# 按维度求和
C