acm-(贪心、思维)Educational Codeforces Round 99 (Rated for Div. 2) E. Four Points

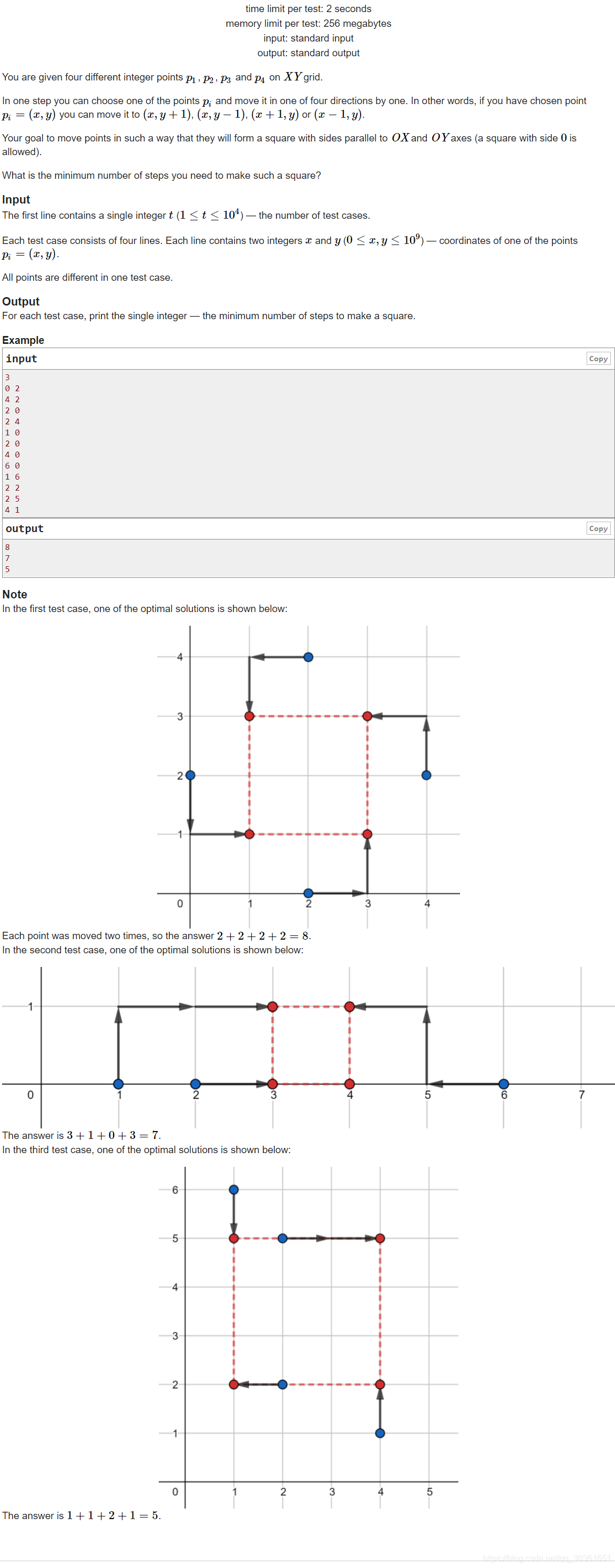
传送门
本题考虑枚举每个点到达正方形的位置(左上角、右上角、左下角、右下角)，总共有$4!$种可能，对于每种可能而言，假设去左上角、右上角、左下角、右下角的点分别用$1、2、3、4$表示，先分别考虑$x、y$的贡献，设 x 1 ′ = m i n { x 1 , x 3 } , x 2 ′ = m a x { x 1 , x 3 } , x 3 ′ = m i n { x 2 , x 4 } , x 4 ′ = m a x { x 2 , x 4 } x_1'=min\{x_1,x_3\},x_2'=max\{x_1,x_3\},x_3'=min\{x_2,x_4\},x_4'=max\{x_2,x_4\} x1′​=min{x1​,x3​},x2′​=max{x1​,x3​},x3′​=min{x2​,x4​},x4′​=max{x2​,x4​}，我们发现若$x_1,x_3$到达$[x_1^{\prime },x_2^{\prime }]$中的无论哪个位置，贡献为$x_2^{\prime }-x_1^{\prime }$；$x_2,x_4$则无论到达$[x_3^{\prime },x_4^{\prime }]$中的哪个位置贡献为$x_4^{\prime }-x_3^{\prime }$，因此我们正方形上下边的长度的区间范围是 [ m a x { x 3 ′ − x 2 ′ , 0 } , m a x { x 4 ′ − x 1 ′ , 0 } ] [max\{x_3'-x_2',0\},max\{x_4'-x_1',0\}] [max{x3′​−x2′​,0},max{x4′​−x1′​,0}]，简写为$[lx,rx]$，在这个范围中我们发现点在移动的过程中$x$轴层次上产生的贡献恒定为$valx=x_4^{\prime }-x_3^{\prime }+x_2^{\prime }-x_1^{\prime }$。不过有个特殊情况是，若$x_4^{\prime }<x_1^{\prime }$，那么$x_1,x_3$到达$[x_1^{\prime },x_2^{\prime }]$的同时$x_2,x_4$无法到达$[x_2^{\prime },x_3^{\prime }]$，此时容易发现有$lx=rx=0,valx=x_4-x_1+x_3-x_2$。

同样地，利用上述方法可以求出$ly,ry,valy$。

如果题目让求一个矩形的话，本题已经做完了，答案就是$valy+valx$，不过本题要求必须是正方形，因此得让两边的长度相同，我们发现若$[lx,rx]$与$[ly,ry]$存在交集，说明两个维度上可以通过适当调节使得正方形边长相等，且$valx,valy$维持不变。不过当两个区间不存在交集的时候，我们一定会改变某一个维度的边长来使得跟另一个维度的边长相等，假设$ry<lx$，那么我们只需要让$y$轴上的边长变成$lx$即可，这样的话需要$valy+=2(lx-ry)$，也就是价值会多出一部分，另一个对称情况是$rx<ly$，这样需要$valx+=2(ly-rx)$。

struct Point{
	ll x,y;
};
int main(){
	int t=rd();
	while(t--){
		Point a[4];
		FOR(i,0,4)a[i].x=rd(),a[i].y=rd();
		int b[4]={0,1,2,3};
		ll ans=INF;
		do{
			ll x1=min(a[b[0]].x,a[b[2]].x),x2=max(a[b[0]].x,a[b[2]].x),x3=min(a[b[1]].x,a[b[3]].x),x4=max(a[b[1]].x,a[b[3]].x);
			ll y1=min(a[b[2]].y,a[b[3]].y),y2=max(a[b[2]].y,a[b[3]].y),y3=min(a[b[0]].y,a[b[1]].y),y4=max(a[b[0]].y,a[b[1]].y);
			ll lx=0,rx=0,ly,ry,valx,valy;
			if(x4<x1){
				valx=x1-x4+x2-x3;
				lx=rx=0;
			}else{
				valx=x4-x3+x2-x1;
				lx=max(x3-x2,0ll);
				rx=x4-x1;
			}
			if(y4<y1){
				valy=y1-y4+y2-y3;
				ly=ry=0;
			}else{
				valy=y4-y3+y2-y1;
				ly=max(y3-y2,0ll);
				ry=y4-y1;
			}
			if(lx<=ry && rx>=ly)ans=min(ans,valx+valy);
			else if(rx<ly)ans=min(ans,valx+valy+2*(ly-rx));
			else ans=min(ans,valx+valy+2*(lx-ry));
		}while(next_permutation(b,b+4));
		printf("%lld\n",ans);
	}
}