线性回归属于监督学习:先给定一个训练集,根据这个训练集学习出一个线性函数,然后通过样本测试这个函数训练的好不好(即此函数是否足够拟合训练集数据),最后挑选出最好的函数(cost最小)。
在样本集中,假设样本是单线性回归的(自变量只有一个)。则我们给出变量线性回归的模型:
x是特征,h(x)是假设性函数。
代价函数:
m为训练样本的个数。
我们的目的,就是要通过不断调整:θ0,θ1,使得代价函数取向最小值。
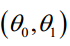
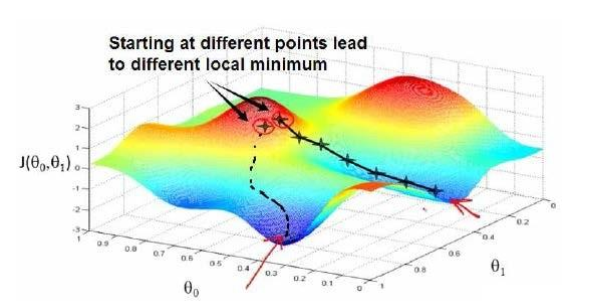
θ0,θ1 要同时调整才能满足微分上的意义,否则,在θ0,θ1相关的代价函数在三维上,并不是在任意方向上实现梯度递减,而是在θ0,θ1两个坐标轴方将以此实现梯度递减。
可视化如图:
这里我们通过批量梯度下降(batch gradient descent)算法来对θ0,θ1进行更新:
在单特征的线性回归中,即有:
代价函数:
function J = computeCost(X, y, theta)
m = length(y); %训练样本个数
J = 0;
J = sum((X * theta - y).^2) / (2*m); % X(79,2) theta(2,1)
end
梯度递减函数:
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s=theta;
for iter = 1:num_iters
theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);
theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));
theta_s=theta; % 用theta_s存储上次结果。
J_history(iter) = computeCost(X, y, theta);
end
J_history
end







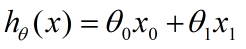
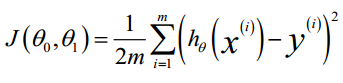
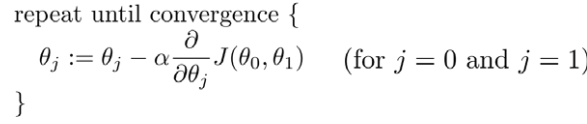
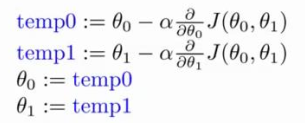














 519
519

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








