Android动画的开发中，为了达到更加酷炫的效果，常常需要自定义运动轨迹，或者绘制花式复杂的曲线，这正是Bezier曲线大显神通的地方，本文将带你了解Bezier曲线在Android开发中的一些应用。
1. Bezier曲线简介
贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。主要结构：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。
根据控制点数目的不同，Bezier曲线可以分为很多种，控制点越多曲线就更复杂，一般常用的是二阶和三阶Bezier曲线，Bezier曲线的具体信息可以参看百科:Constructing Bézier curves
1.1 一阶Bezier曲线
为了便于理解，我们先从一阶Bezier曲线开始。由两个点控制的曲线，也就是一条直线.
一阶Bezier曲线1.2 二阶Bezier曲线
由三个点控制的曲线。P0是起点，P2是终点。P1是控制点，t是一个系数，表示从0-1的变化过程，红色的线就是最终画出的曲线。
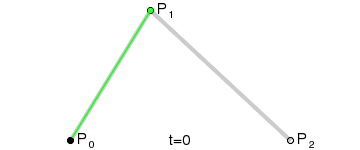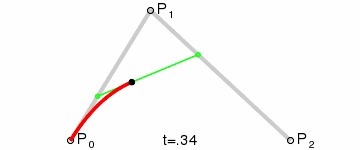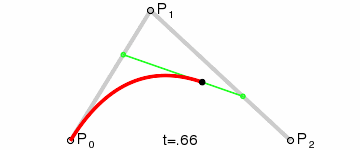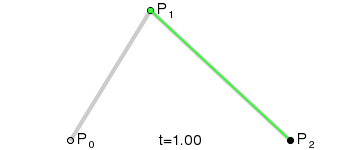二阶Bezier曲线原理:
- 由 P0 至 P1 的连续点 Q0，描述一条线段。
- 由 P1 至 P2 的连续点 Q1，描述一条线段。
- 由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。
1.3 三阶Bezier曲线
三阶贝塞尔曲线和二阶的有限类似，只不过除了一个起点和一个终点，同时由两个控制点来控制：
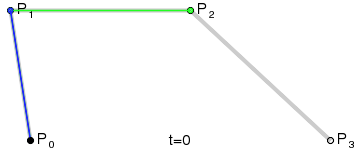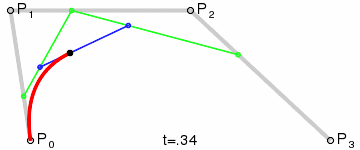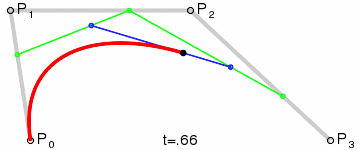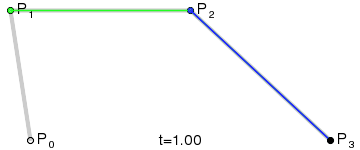三阶Bezier曲线当然还有更高阶的Bezier曲线，这里就不一一展开说明了，总之控制点越多，曲线就越复杂。更多关于Bezier曲线的内容可以查看：贝塞尔曲线扫盲。
2. 如何绘制Bezier曲线
请各位读者不要被数学公式吓退，在实际的工程应用中，最多使用的都是二阶和三阶Bezier曲线，更高阶的曲线可以通过使用二阶和三阶的曲线组合来实现，这样更为简单高效。
在Android中的Path类中，提供了API来绘制二阶和三阶Bezier曲线
2.1 绘制二阶Bezier曲线
/** * 从上一个点开始，绘制二阶Bezier曲线 * (x1,y1)为控制点， (x2,y2)为终点 * 如果之前没有调用过 moveTo()，则默认从 (0,0)作为起点绘制。 */ public void quadTo(float x1, float y1, float x2, float y2) ； /** * 和quadTo相同，只不过这里是使用的是相对坐标。 */ public void rQuadTo(float dx1, float dy1, float dx2, float dy2)绘制效果如下，为了便于读者理解，加上了辅助线和辅助点。
二阶Bezier曲线2.2 绘制三阶Bezier曲线
/** * 从上一个点开始，绘制三阶Bezier曲线 * (x1,y1)，(x2,y2)为控制点， (x3,x3)为终点 * 如果之前没有调用过 moveTo()，则默认从 (0,0)作为起点绘制。 */ public void cubicTo(float x1, float y1, float x2, float y2, float x3, float y3) /** * 和rCubicTo相同，只不过这里是使用的是相对坐标。 */ public void rCubicTo(float x1, float y1, float x2, float y2, float x3, float y3)绘制效果如下，为了便于读者理解，加上了辅助线和辅助点。
三阶Bezier曲线
三阶Bezier曲线3 利用Bezier曲线产生运动轨迹
绘制Bezier曲线很容易，但是希望利用Bezier曲线自定义运动轨迹该怎么做呢？这就需要先想办法取出Bezier曲线上的点。
3.1 在Bezier曲线上取点
Bezier曲线在游戏制作中已经有了十分广泛的应用，所以在Bezier曲线上取点也是个经常被提到的问题。感谢前人的数学公式的终结，我们可以按照如下方法,以长度比例取出Bezier曲线上的对应的点。
public class BezierUtil { /** * B(t) = (1 - t)^2 * P0 + 2t * (1 - t) * P1 + t^2 * P2, t ∈ [0,1] * * @param t 曲线长度比例 * @param p0 起始点 * @param p1 控制点 * @param p2 终止点 * @return t对应的点 */ public static PointF CalculateBezierPointForQuadratic(float t, PointF p0, PointF p1, PointF p2) { PointF point = new PointF(); float temp = 1 - t; point.x = temp * temp * p0.x + 2 * t * temp * p1.x + t * t * p2.x; point.y = temp * temp * p0.y + 2 * t * temp * p1.y + t * t * p2.y; return point; } /** * B(t) = P0 * (1-t)^3 + 3 * P1 * t * (1-t)^2 + 3 * P2 * t^2 * (1-t) + P3 * t^3, t ∈ [0,1] * * @param t 曲线长度比例 * @param p0 起始点 * @param p1 控制点1 * @param p2 控制点2 * @param p3 终止点 * @return t对应的点 */ public static PointF CalculateBezierPointForCubic(float t, PointF p0, PointF p1, PointF p2, PointF p3) { PointF point = new PointF(); float temp = 1 - t; point.x = p0.x * temp * temp * temp + 3 * p1.x * t * temp * temp + 3 * p2.x * t * t * temp + p3.x * t * t * t; point.y = p0.y * temp * temp * temp + 3 * p1.y * t * temp * temp + 3 * p2.y * t * t * temp + p3.y * t * t * t; return point; } }3.2 使用实例
下面我们用一个实例来给大家解释如何使用上面的方法。 我们要绘制一个二阶Bezier曲线：点击屏幕并移动手指时，将会改变曲线的控制点的坐标；当抬起手指时，一个圆形将会沿着该Bezier曲线从起点运行到重点。
我们先看下完整的代码：
/** * Created by Sun Rongxin on 2017/6/3. * to show how a quad-Bezier curve is generated by 3 points * and how to get points on the quad-Bezier curve. */ public class QuadBezierView extends View { /** * 起点坐标 */ private float mStartPointX; private float mStartPointY; /** * 重点坐标 */ private float mEndPointX; private float mEndPointY; /** * 控制点 */ private float mCtrlPointX; private float mCtrlPointY; private Path mPath; /** * 移动坐标 */ private float mMovePointX; private float mMovePointY; /** * 画曲线所用的画笔 */ private Paint mPaintBezier; /** * 话辅助线所用的画笔 */ private Paint mPaintCtrl; /** * 绘制文字的画笔 */ private Paint mPaintText; /** * 绘制运动圆圈的画笔 */ private Paint mPaintCircle; public QuadBezierView(Context context) { super(context); } public QuadBezierView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) { super(context, attrs, defStyleAttr); } public QuadBezierView(Context context, @Nullable AttributeSet attrs) { super(context, attrs); //初始化画笔 mPaintBezier = new Paint(Paint.ANTI_ALIAS_FLAG); mPaintBezier.setStrokeWidth(3);//划线的宽度 mPaintBezier.setStyle(Paint.Style.STROKE);//画笔的类型，这里是实线 mPaintCtrl = new Paint(Paint.ANTI_ALIAS_FLAG); mPaintCtrl.setStrokeWidth(1); mPaintCtrl.setStyle(Paint.Style.STROKE); mPaintText = new Paint(Paint.ANTI_ALIAS_FLAG); mPaintText.setStyle(Paint.Style.STROKE); mPaintText.setTextSize(20); mPaintCircle = new Paint(Paint.ANTI_ALIAS_FLAG); } /** *在每次View的Size变化时，设定曲线的起点、终点以及控制点，并绘制曲线 */ @Override protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); mStartPointX = w / 10; mStartPointY = h / 2 - 200; mEndPointX = w * 9 / 10; mEndPointY = h / 2 - 200; mCtrlPointX = w / 2; mCtrlPointY = h / 2 - 300; mMovePointX = mStartPointX; mMovePointY = mStartPointY; mPath = new Path(); } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); //绘制曲线 mPath.reset(); mPath.moveTo(mStartPointX,mStartPointY); mPath.quadTo(mCtrlPointX, mCtrlPointY,mEndPointX,mEndPointY); canvas.drawPath(mPath,mPaintBezier); ///绘制起点、终点和控制点 canvas.drawPoint(mStartPointX, mStartPointY, mPaintCtrl); canvas.drawPoint(mEndPointX, mEndPointY, mPaintCtrl); canvas.drawPoint(mCtrlPointX, mCtrlPointY, mPaintCtrl); //加上文字注解 canvas.drawText("起点", mStartPointX, mStartPointY, mPaintText); canvas.drawText("终点", mEndPointX, mEndPointY, mPaintText); canvas.drawText("控制点", mCtrlPointX, mCtrlPointY, mPaintText); //绘制辅助线 canvas.drawLine(mStartPointX, mStartPointY, mCtrlPointX, mCtrlPointY, mPaintCtrl); canvas.drawLine(mEndPointX, mEndPointY, mCtrlPointX, mCtrlPointY, mPaintCtrl); canvas.drawCircle(mMovePointX, mMovePointY, 20, mPaintCircle); } @Override public boolean onTouchEvent(MotionEvent event) { switch (event.getAction()){ case MotionEvent.ACTION_MOVE:{ mCtrlPointX = event.getX(); mCtrlPointY = event.getY(); //表示当前View失效，如View是可见的，则onDraw方法会被调用 //注意：该方法需要在UI线程中执行 invalidate(); break; } case MotionEvent.ACTION_UP:{ mCtrlPointX = event.getX(); mCtrlPointY = event.getY(); ValueAnimator valueAnimator = ValueAnimator.ofFloat(0,1); valueAnimator.setDuration(2000).addUpdateListener(new ValueAnimator.AnimatorUpdateListener() { @Override public void onAnimationUpdate(ValueAnimator animation) { float t = (float) animation.getAnimatedValue(); PointF p = BezierUtil.CalculateBezierPointForQuadratic(t, new PointF(mStartPointX, mStartPointY), new PointF(mCtrlPointX, mCtrlPointY), new PointF(mEndPointX, mEndPointY) ); mMovePointX = (int) p.x; mMovePointY = (int) p.y; //重新绘制View invalidate(); } }); valueAnimator.setInterpolator(new AccelerateDecelerateInterpolator()); valueAnimator.start(); break; } } //表示该事件已经被消耗 return true; } }请大家重点关注onTouchEvent方法中MotionEvent.ACTION_UP对应的部分：
//手指抬起时，圆形开始移动 case MotionEvent.ACTION_UP:{ //获得当前的控制点 mCtrlPointX = event.getX(); mCtrlPointY = event.getY(); //设置变化区间 ValueAnimator valueAnimator = ValueAnimator.ofFloat(0,1); valueAnimator.setDuration(2000).addUpdateListener(new ValueAnimator.AnimatorUpdateListener() { @Override public void onAnimationUpdate(ValueAnimator animation) { //获得当前比例值 float t = (float) animation.getAnimatedValue(); //计算当前点坐标 PointF p = BezierUtil.CalculateBezierPointForQuadratic(t, new PointF(mStartPointX, mStartPointY), new PointF(mCtrlPointX, mCtrlPointY), new PointF(mEndPointX, mEndPointY) ); mMovePointX = (int) p.x; mMovePointY = (int) p.y; //重新绘制View invalidate(); } }); valueAnimator.setInterpolator(new AccelerateDecelerateInterpolator()); valueAnimator.start(); break; }这里利用ValueAnimator在[0,1]区间上逐渐变大，同时设置监听器在每次取值变化时，利用上面给出的 BezierUtil.CalculateBezierPointForQuadratic方法计算出曲线上对应比例点的坐标，并以此点坐标为圆心绘制圆形。通过不断地获得曲线上不同点而绘制圆形，就达到了圆形在曲线上运动的效果。
运行效果：
bezier_curve.gif多个Bezier曲线组合-水波纹
上面说过，复杂的曲线都可以通过多个Bezier曲线组合的形式来展现出来，下面我们就来实战一个例子，用两个二阶Bezier曲线绘制水波纹。
水波纹有高有低，类似于sin函数的图片，有周期性。凸出的部分是一个Bezier曲线，凹进的部分是另一个曲线：
mPath.moveTo(mOffset, mCenterY); //控制点在波峰处上方 mPath.quadTo(mWaveLength / 4 + mOffset, mCenterY + 60, mWaveLength / 2 + mOffset, mCenterY); //控制点在波谷处下方 mPath.quadTo(mWaveLength * 3 / 4 + mOffset, mCenterY - 60, mWaveLength +mOffset, mCenterY);其中mOffset是初始的绘制的起始坐标，mWaveLength完整周期的波长，mCenterY是Y轴方向上的中线。
想要波光粼粼的效果，我们还需要让水波移动起来。聪明的读者可能已经想到，没错，就是改变起始位置的偏移量mOffset。
@Override public void onClick(View v) { //点击View,开始动画 mValueAnimator = ValueAnimator.ofInt(0, mWaveLength); mValueAnimator.setDuration(1000); mValueAnimator.setRepeatCount(ValueAnimator.INFINITE); mValueAnimator.setInterpolator(new LinearInterpolator()); //更新偏移量 mValueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() { @Override public void onAnimationUpdate(ValueAnimator valueAnimator) { mOffset = (int) valueAnimator.getAnimatedValue(); invalidate(); } }); mValueAnimator.start(); }当点击View时，启动插值器在[0,WaveLength]之间递增取值，这就是我们需要的位移量。
屏幕的宽度可能容纳多个波长，所以我们还需要确定需要绘制几个完整的波形。这里需要说明的,波纹从左到右移动，那么就需要在屏幕外左侧绘制一个完整的波形，以保证向右移动的过程中，波形是连绵不断的。
//计算需要绘制几个完整的波形，注意需要多绘制一个完整的波形用来位移，多出来0.5是防止被四舍五入 mWaveCount = (int) Math.round(mScreenWidth / mWaveLength + 1.5);完整的代码如下：
public class WaveView extends View implements View.OnClickListener{ private int mWaveLength; //波长 private int mScreenHeight; //屏幕高 private int mScreenWidth; //屏幕宽 private int mCenterY; //Y轴上的重点 private int mWaveCount; //屏幕上能显示完整波形的个数 private int mOffset; //波形绘制的偏移量 private ValueAnimator mValueAnimator; //改变 mOffSet的插值器 private Paint mPaintBezier; //绘制波纹的画笔1 private Path mPath; //绘制波纹的路径1 public WaveView(Context context) { super(context); } public WaveView(Context context, @Nullable AttributeSet attrs) { super(context, attrs); mPaintBezier = new Paint(Paint.ANTI_ALIAS_FLAG); mPaintBezier.setColor(Color.LTGRAY); mPaintBezier.setStrokeWidth(8); mPaintBezier.setStyle(Paint.Style.FILL_AND_STROKE); mWaveLength = 800; } public WaveView(Context context, @Nullable AttributeSet attrs, int defStyleAttr) { super(context, attrs, defStyleAttr); } public WaveView(Context context, @Nullable AttributeSet attrs, int defStyleAttr, int defStyleRes) { super(context, attrs, defStyleAttr, defStyleRes); } protected void onSizeChanged(int w, int h, int oldw, int oldh) { super.onSizeChanged(w, h, oldw, oldh); mPath = new Path(); setOnClickListener(this); mScreenHeight = h; mScreenWidth = w; mCenterY = h / 2; //计算需要绘制几个完整的波形，注意需要多绘制一个完整的波形用来位移，多出来0.5是防止被四舍五入 mWaveCount = (int) Math.round(mScreenWidth / mWaveLength + 1.5); } @Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPath.reset(); //位移到屏幕外左侧一个波长的地方，开始绘制水波 mPath.moveTo(-mWaveLength + mOffset, mCenterY); //利用两个Bezier曲线绘制出水波 for (int i = 0; i < mWaveCount; i++) { int totalOffSet = i * mWaveLength + mOffset; //控制点在波峰处上方 mPath.quadTo(-mWaveLength * 3 / 4 + totalOffSet, mCenterY + 60, -mWaveLength / 2 + totalOffSet, mCenterY); //控制点在波谷处下方 mPath.quadTo(-mWaveLength / 4 + totalOffSet, mCenterY - 60, totalOffSet, mCenterY); } //闭合图象，并填充 mPath.lineTo(mScreenWidth, mScreenHeight); mPath.lineTo(0, mScreenHeight); mPath.close(); canvas.drawPath(mPath, mPaintBezier); } @Override public void onClick(View v) { //点击View,开始动画 mValueAnimator = ValueAnimator.ofInt(0, mWaveLength); mValueAnimator.setDuration(1000); mValueAnimator.setRepeatCount(ValueAnimator.INFINITE); mValueAnimator.setInterpolator(new LinearInterpolator()); //更新位移量 mValueAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() { @Override public void onAnimationUpdate(ValueAnimator valueAnimator) { mOffset = (int) valueAnimator.getAnimatedValue(); invalidate(); } }); mValueAnimator.start(); } }水波纹的动画效果
wave.gif最后给出整个工程的GItHub代码下载地址,欢迎大家下载、fork和给星！
作者：登高且赋
链接：http://www.jianshu.com/p/fea4d1f6512a
來源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
扫一扫
995
评论
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
查看更多评论
添加红包
