神经网络入门 —— 感知机

本章将介绍感知机 , 严格地讲，本章中所说的感知机应该称为“人工神经元”或“朴素感知机”，但是因为很多基本的处理都是共通的，所以这里就简单地称为“感知机”。感知机是由美国学者 Frank Rosenblatt 在 1957 年提出来的。为何我们现在还要学习这一很久以前就有的算法呢？因为感知机也是作为神经网络（深度学习）的起源的算法。因此，学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。

2.1 感知机是什么

感知机接收多个输入信号，输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。像电流流过导线，向前方输送电子一样，感知机的信号也会形成流，向前方输送信息。但是，和实际的电流不同的是，感知机的信号只有“流 / 不流”（1/0）两种取值。在本书中，0 对应“不传递信号”，1 对应“传递信号”。

图 2-1 是一个接收两个输入信号的感知机的例子。x₁ ，x₂是输入信号，y 是输出信号，w₁ ，w₂是权重（w是 weight 的首字母）。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时，会被分别乘以固定的权重（w₁ x₁、w₂ x₂）。神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出 1。这也称为“神经元被激活”。这里将这个界限值称为阈值，用符号 θ 表示。

图 2-1

感知机的运行原理只有这些！把上述内容用数学式来表示，就是式（2.1）。

感知机的多个输入信号都有各自固有的权重，这些权重发挥着控制各个信号的重要性的作用。也就是说，权重越大，对应该权重的信号的重要性就越高。

权重相当于电流里所说的电阻。电阻是决定电流流动难度的参数，电阻越低，通过的电流就越大。而感知机的权重则是值越大，通过的信号就越大。不管是电阻还是权重，在控制信号流动难度（或者流动容易度）这一点上的作用都是一样的。

2.2 简单逻辑电路

2.2.1 与门

现在让我们考虑用感知机来解决简单的问题。这里首先以逻辑电路为题材来思考一下与门（AND gate）。与门是有两个输入和一个输出的门电路。图 2-2 这种输入信号和输出信号的对应表称为“真值表”。如图 2-2 所示，与门仅在两个输入均为 1 时输出 1，其他时候则输出 0。

图 2-2

下面考虑用感知机来表示这个与门。需要做的就是确定能满足图 2-2 的真值表的 w₁ 、w₂、θ 的值。那么，设定什么样的值才能制作出满足图 2-2 的条件的感知机呢？

实际上，满足图 2-2 的条件的参数的选择方法有无数多个。比如，当（w₁，w₂，θ）= （0.5，0.5，0.7）时，可以满足图 2-2 的条件。此外，当（w₁，w₂，θ）为 (0.5, 0.5, 0.8) 或者 (1.0, 1.0, 1.0) 时，同样也满足与门的条件。设定这样的参数后，仅当 x₁ ，x₂同时为 1 时，信号的加权总和才会超过给定的阈值 θ。

2.2.2　与非门和或门

接着，我们再来考虑一下与非门（NAND gate）。NAND 是 Not AND 的意思，与非门就是颠倒了与门的输出。用真值表表示的话，如图 2-3 所示，仅当 x₁和 x₂ 同时为 1 时输出 0，其他时候则输出 1。那么与非门的参数又可以是什么样的组合呢？

图 2-3

要表示与非门，可以用（w₁，w₂，θ）= (-0.5,-0.5,-0.7) 这样的组合（其他的组合也是无限存在的）。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门。 接下来看一下图 2-4 所示的或门。或门是“只要有一个输入信号是 1，输出就为 1”的逻辑电路。那么我们来思考一下，应该为这个或门设定什么样的参数呢？

图 2-4

这里决定感知机参数的并不是计算机，而是我们人。我们看着真值表这种“训练数据”，人工考虑（想到）了参数的值。而机器学习的课题就是将这个决定参数值的工作交由计算机自动进行。学习是确定合适的参数的过程，而人要做的是思考感知机的构造（模型），并把训练数据交给计算机。

如上所示，我们已经知道使用感知机可以表示与门、与非门、或门的逻辑电路。这里重要的一点是：与门、与非门、或门的感知机构造是一样的。实际上，3 个门电路只有参数的值（权重和阈值）不同。也就是说，相同构造的感知机，只需通过适当地调整参数的值，就可以像“变色龙演员”表演不同的角色一样，变身为与门、与非门、或门。

2.3 感知机的实现

2.3.1　简单的实现

现在，我们用 Python 来实现刚才的逻辑电路。这里，先定义一个接收参数 x1 和 x2 的 AND 函数。

# coding: utf-8
import numpy as np

w1, w2, theta = 0.5,0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
	return 0
elif tmp > theta:
    return 1

在函数内初始化参数w1、w2、theta，当输入的加权总和超过阈值时返回 1，否则返回 0。我们来确认一下输出结果是否如图 2-2 所示。

AND  1  # 输出0
AND  0  # 输出0
AND  1  # 输出1

果然和我们预想的输出一样！这样我们就实现了与门。按照同样的步骤，也可以实现与非门和或门，不过让我们来对它们的实现稍作修改。

2.3.2　导入权重和偏置

刚才的与门的实现比较直接、容易理解，但是考虑到以后的事情，我们将其修改为另外一种实现形式。在此之前，首先把式（2.1）的 θ 换成 -b，于是就可以用式（2.2）来表示感知机的行为。

式（2.1）和式（2.2）虽然有一个符号不同，但表达的内容是完全相同的。此处，b 称为偏置，w₁，w₂ 称为权重。如式（2.2）所示，感知机会计算输入信号和权重的乘积，然后加上偏置，如果这个值大于 0 则输出 1，否则输出 0。下面，我们使用 NumPy，按式（2.2）的方式实现感知机。在这个过程中，我们用 Python 的解释器逐一确认结果。

>>> import numpy as np
>>> x = np.array([0, 1])    	# 输入
>>> w = np.array([0.5, 0.5]) 	# 权重
>>> b = -0.7</b>                # 偏置
>>> w*x
array([ 0. , 0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x) + b<
-0.19999999999999996   # 大约为-0.2（由浮点小数造成的运算误差）

如上例所示，在 NumPy 数组的乘法运算中，当两个数组的元素个数相同时，各个元素分别相乘，因此 w*x 的结果就是它们的各个元素分别相乘（[0, 1] * [0.5, 0.5] => [0, 0.5]）。之后，np.sum(w*x) 再计算相乘后的各个元素的总和。最后再把偏置加到这个加权总和上，就完成了式（2.2）的计算。

2.3.3　使用权重和偏置的实现

使用权重和偏置，可以像下面这样实现与门。

# coding: utf-8
import numpy as np


def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

这里把 -θ 命名为偏置 b，但是请注意，偏置和权重 w₁，w₂的作用是不一样的。具体地说，w₁，w₂是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为 1 的程度）的参数。比如，若 b 为 -0.1，则只要输入信号的加权总和超过 0.1，神经元就会被激活。但是如果 b 为 -20.0，则输入信号的加权总和必须超过 20.0，神经元才会被激活。像这样，偏置的值决定了神经元被激活的容易程度。另外，这里我们将 w₁，w₂称为权重，将 b 称为偏置，但是根据上下文，有时也会将 b、w₁，w₂ 这些参数统称为权重。

偏置这个术语，有“穿木屐”(因为木屐的底比较厚，穿上它后，整个人也会显得更高。——译者注)的效果，即在没有任何输入时（输入为 0 时），给输出穿上多高的木屐（加上多大的值）的意思。实际上，在式 (2.2) 的计算中，当输入x₁ ，x₂ 为 0 时，只输出偏置的值。

接着，我们继续实现与非门和或门。

def NAND(x1, x2):
    x = np.array([x1, x2])
    <b>w = np.array([-0.5, -0.5])</b> # 仅权重和偏置与AND不同！
    <b>b = 0.7</b>
    tmp = np.sum(w*x) + b
    if tmp &lt;= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    <b>w = np.array([0.5, 0.5])</b> # 仅权重和偏置与AND不同！
    <b>b = -0.2</b>
    tmp = np.sum(w*x) + b
    if tmp &lt;= 0:
        return 0
    else:
        return 1

我们在 2.2 节介绍过，与门、与非门、或门是具有相同构造的感知机，区别只在于权重参数的值。因此，在与非门和或门的实现中，仅设置权重和偏置的值这一点和与门的实现不同。

2.4 感知机的局限性

到这里我们已经知道，使用感知机可以实现与门、与非门、或门三种逻辑电路。现在我们来考虑一下异或门（XOR gate）。

2.4.1 异或门

异或门也被称为逻辑异或电路。如图 2-5 所示，仅当 x₁ 或 x₂ 中的一方为 1 时，才会输出 1（“异或”是拒绝其他的意思）。那么，要用感知机实现这个异或门的话，应该设定什么样的权重参数呢？

图 2-5

实际上，用前面介绍的感知机是无法实现这个异或门的。为什么用感知机可以实现与门、或门，却无法实现异或门呢？下面我们尝试通过画图来思考其中的原因。

首先，我们试着将或门的动作形象化。或门的情况下，当权重参数 (b， w₁，w₂) = (-0.5,1.0,1.0) 时，可满足图 2-4 的真值表条件。此时，感知机可用下面的式（2.3）表示。


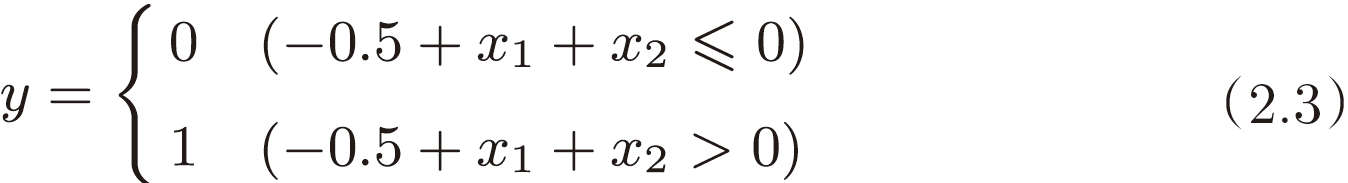式（2.3）表示的感知机会生成由直线 -0.5 + x₁ +x₂ = 0 分割开的两个空间。其中一个空间输出 1，另一个空间输出 0，如图 2-6 所示。

图 2-6

或门在(x₁, x₂) = (0, 0) 时输出 0，在 (x₁, x₂) 为 (0, 1)、(1, 0)、(1, 1) 时输出 1。图 2-6 中，○ 表示 0，△ 表示 1。如果想制作或门，需要用直线将图 2-6 中的○和△分开。实际上，刚才的那条直线就将这 4 个点正确地分开了。

那么，换成异或门的话会如何呢？能否像或门那样，用一条直线作出分割图 2-7 中的○和△的空间呢？

图 2-7

想要用一条直线将图 2-7 中的○和△分开，无论如何都做不到。事实上，用一条直线是无法将○和△分开的。

2.4.2　线性和非线性

图 2-7 中的○和△无法用一条直线分开，但是如果将“直线”这个限制条件去掉，就可以实现了。比如，我们可以像图 2-8 那样，作出分开○和△的空间。

图 2-8

感知机的局限性就在于它只能表示由一条直线分割的空间。图 2-8 这样弯曲的曲线无法用感知机表示。另外，由图 2-8 这样的曲线分割而成的空间称为非线性空间，由直线分割而成的空间称为线性空间。线性、非线性这两个术语在机器学习领域很常见，可以将其想象成图 2-6 和图 2-8 所示的直线和曲线。

2.5 多层感知机

感知机不能表示异或门让人深感遗憾，但也无需悲观。实际上，感知机的绝妙之处在于它可以“叠加层”（通过叠加层来表示异或门是本节的要点）。这里，我们暂且不考虑叠加层具体是指什么，先从其他视角来思考一下异或门的问题。

2.5.1　已有门电路的组合

异或门的制作方法有很多，其中之一就是组合我们前面做好的与门、与非门、或门进行配置。这里，与门、与非门、或门用图 2-9 中的符号表示。另外，图 2-9 中与非门前端的○表示反转输出的意思。

图 2-9

那么，请思考一下，要实现异或门的话，需要如何配置与门、与非门和或门呢？这里给大家一个提示，用与门、与非门、或门代替图 2-10 中的各个“？”，就可以实现异或门。


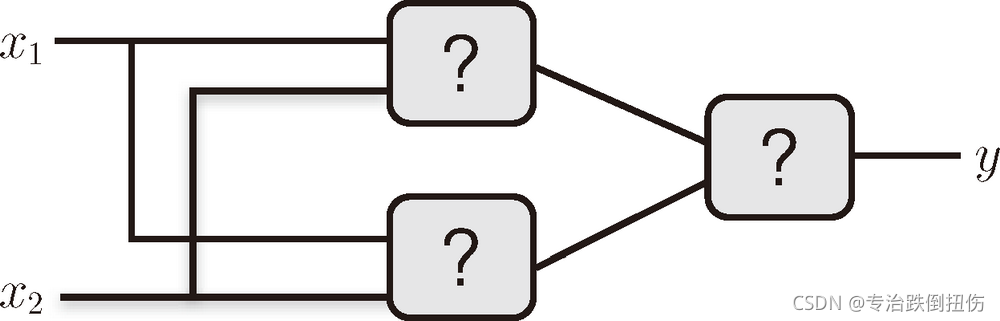2.4 节讲到的感知机的局限性，严格地讲，应该是“单层感知机无法表示异或门”或者“单层感知机无法分离非线性空间”。接下来，我们将看到通过组合感知机（叠加层）就可以实现异或门。

异或门可以通过图 2-11 所示的配置来实现。这里，x₁ 和 x₂表示输入信号，y 表示输出信号。x₁ 和 x₂ 是与非门和或门的输入，而与非门和或门的输出则是与门的输入。

图 2-11

现在，我们来确认一下图 2-11 的配置是否真正实现了异或门。这里，把 S₁ 作为与非门的输出，把 S₂ 作为或门的输出，填入真值表中。结果如图 2-12 所示，观察 x₁、x₂、y，可以发现确实符合异或门的输出。

图 2-12

2.5.2　异或门的实现

下面我们试着用 Python 来实现图 2-11 所示的异或门。使用之前定义的 AND 函数、NAND 函数、OR 函数，可以像下面这样（轻松地）实现。

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

这个 XOR 函数会输出预期的结果。

XOR(0, 0) # 输出0
XOR(1, 0) # 输出1
XOR(0, 1) # 输出1
XOR(1, 1) # 输出0

这样，异或门的实现就完成了。下面我们试着用感知机的表示方法（明确地显示神经元）来表示这个异或门，结果如图 2-13 所示。

图 2-13

如图 2-13 所示，异或门是一种多层结构的神经网络。这里，将最左边的一列称为第 0 层，中间的一列称为第 1 层，最右边的一列称为第 2 层。

图 2-13 中的感知机总共由 3 层构成，但是因为拥有权重的层实质上只有 2 层（第 0 层和第 1 层之间，第 1 层和第 2 层之间），所以称为“2 层感知机”。不过，有的文献认为图 2-13 的感知机是由 3 层构成的，因而将其称为“3 层感知机”。

在图 2-13 所示的 2 层感知机中，先在第 0 层和第 1 层的神经元之间进行信号的传送和接收，然后在第 1 层和第 2 层之间进行信号的传送和接收，具体如下所示。

1. 第 0 层的两个神经元接收输入信号，并将信号发送至第 1 层的神经元。
2. 第 1 层的神经元将信号发送至第 2 层的神经元，第 2 层的神经元输出 y。

这种 2 层感知机的运行过程可以比作流水线的组装作业。第 1 段（第 1 层）的工人对传送过来的零件进行加工，完成后再传送给第 2 段（第 2 层）的工人。第 2 层的工人对第 1 层的工人传过来的零件进行加工，完成这个零件后出货（输出）。

像这样，在异或门的感知机中，工人之间不断进行零件的传送。通过这样的结构（2 层结构），感知机得以实现异或门。这可以解释为“单层感知机无法表示的东西，通过增加一层就可以解决”。也就是说，通过叠加层（加深层），感知机能进行更加灵活的表示。

2.6　从与非门到计算机

多层感知机可以实现比之前见到的电路更复杂的电路。比如，进行加法运算的加法器也可以用感知机实现。此外，将二进制转换为十进制的编码器、满足某些条件就输出 1 的电路（用于等价检验的电路）等也可以用感知机表示。实际上，使用感知机甚至可以表示计算机！

计算机是处理信息的机器。向计算机中输入一些信息后，它会按照某种既定的方法进行处理，然后输出结果。所谓“按照某种既定的方法进行处理”是指，计算机和感知机一样，也有输入和输出，会按照某个既定的规则进行计算。

人们一般会认为计算机内部进行的处理非常复杂，而令人惊讶的是，实际上只需要通过与非门的组合，就能再现计算机进行的处理。这一令人吃惊的事实说明了什么呢？说明使用感知机也可以表示计算机。前面也介绍了，与非门可以使用感知机实现。也就是说，如果通过组合与非门可以实现计算机的话，那么通过组合感知机也可以表示计算机（感知机的组合可以通过叠加了多层的单层感知机来表示）。

说到仅通过与非门的组合就能实现计算机，大家也许一下子很难相信。建议有兴趣的读者看一下《计算机系统要素：从零开始构建现代计算机》。这本书以深入理解计算机为主题，论述了通过 NAND构建可运行俄罗斯方块的计算机的过程。此书能让读者真实体会到，通过简单的 NAND元件就可以实现计算机这样复杂的系统。

综上，多层感知机能够进行复杂的表示，甚至可以构建计算机。那么，什么构造的感知机才能表示计算机呢？层级多深才可以构建计算机呢？

理论上可以说 2 层感知机就能构建计算机。这是因为，已有研究证明，2 层感知机（严格地说是激活函数使用了非线性的 sigmoid 函数的感知机，具体请参照下一章）可以表示任意函数。但是，使用 2 层感知机的构造，通过设定合适的权重来构建计算机是一件非常累人的事情。实际上，在用与非门等低层的元件构建计算机的情况下，分阶段地制作所需的零件（模块）会比较自然，即先实现与门和或门，然后实现半加器和全加器，接着实现算数逻辑单元（ALU），然后实现 CPU。因此，通过感知机表示计算机时，使用叠加了多层的构造来实现是比较自然的流程。

本书中不会实际来实现计算机，但是希望读者能够记住，感知机通过叠加层能够进行非线性的表示，理论上还可以表示计算机进行的处理。

2.7　小结

本章我们学习了感知机。感知机是一种非常简单的算法，大家应该很快就能理解它的构造。感知机是下一章要学习的神经网络的基础，因此本章的内容非常重要。

本章所学的内容

• 感知机是具有输入和输出的算法。给定一个输入后，将输出一个既定的值。
• 感知机将权重和偏置设定为参数。
• 使用感知机可以表示与门和或门等逻辑电路。
• 异或门无法通过单层感知机来表示。
• 使用 2 层感知机可以表示异或门。
• 单层感知机只能表示线性空间，而多层感知机可以表示非线性空间。
• 多层感知机（在理论上）可以表示计算机。

附录

本篇是一篇学习笔记 摘录自：《深度学习入门：基于 Python 的理论与实现》——斋藤康毅
编辑不易，各位大佬高抬贵手点点赞！
侵权删