POJ 3525 二分答案，推进多边形和半平面交

转载：http://blog.csdn.net/non_cease/article/details/7814970

题目在问这样一个问题：给定一个凸多边形，找到其中的一个点，使得其到每条边的距离最小值最大，输出这个距离。

其实就是在问你，这个多边形中最大的一个内切圆有多大。

怎么做呢？如果我们事先知道一个半径R，我们是不是能验证这个R是否可行呢？

答案是肯定的，这样想：如果我们把这个多边形每条边都向内推进R，之后如果这个多边形还存在的话，就说明这个半径为R的圆肯定塞得下，因为还可以往里缩嘛。直到他们缩成一个点的时候，这个时候缩的距离就是我们要找的R了，同时这个点也肯定是我们要找的圆的圆心。

那么，我们就可以二分一下R，之后用半平面交判断一下多边形是否还在就行了。

半平面交的实现和求多边形的核一模一样，我们可以考虑这个问题是一堆半平面的交，实际上实现手段是切割已有的答案区域，得到一个更小的答案区域，这就是半平面交的实现手段。为此，我们一开始选择一个肯定要大一些的答案区域，再不断用直线去切割就可以了。

最想说一下什么呢？是“将每条边推进R”应该怎么实现。很多人绕了半天，实际上我找到一个很简单的公式：把直线表示成Ax + By + C = 0后（已考虑顺逆时针所带来的正负号问题），把直线向内推进d时，只需要写：

c += d * sqrt(a*a + b*b);  

就可以了。

为什么呢？我们可以简单推导一下：

①当直线不垂直于X轴的时候，不妨假设直线向左上方移动（直线方向为右上）：

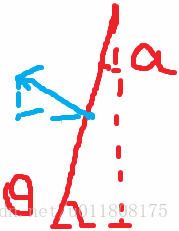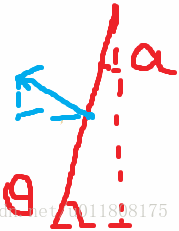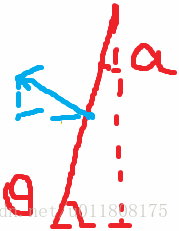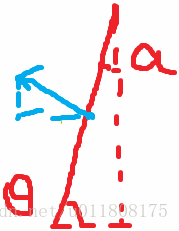
有如下关系成立：

tanθ = k = - A / B

sinα = -B / sqrt( a*a + b*b)

cosα = A / sqrt(a*a + b*b)

dx = d*cosα

dy = d*sinα

新直线方程为A（x+dx） + B（y+dy） + C = 0

拆开整理，会发现分子上面有一个A² + B² ，和下面的sqrt（A² + B²） 约掉一份，得出△C = d* sqrt（A² + B²）。

②当直线垂直于X轴的时候，解析式为Ax + C = 0， 不妨假设直线向左移动（其方向是向上的），则新直线为A（x + d）+ C =0, 于是有△C = Ad = d * sqrt（a*a+b*b）。

代码是我自己的：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
using namespace std;
struct Point
{
	double x, y;
}point[150], temp[150], temp_temp[150];
int num_temp, cut_num;
int n;
double a, b, c;
void getline(Point p2, Point p1)//可以轻松证明出该结论。
{
	a = p1.y - p2.y;
	b = p2.x - p1.x;
	c = p2.y*p1.x - p1.y*p2.x;
}
Point intersect(Point x, Point y) //获取直线ax+by+c==0  和点x和y所连直线的交点
{
	double u = fabs(a*x.x + b*x.y + c);
	double v = fabs(a*y.x + b*y.y + c);
	Point ans;
	ans.x = (x.x*v + y.x*u) / (u + v);
	ans.y = (x.y*v + y.y*u) / (u + v);
	return ans;
}
void cut()
{
	cut_num = 0;
	for (int i = 1; i <= num_temp; i++)
	{
		Point p = temp[i];
		Point p1 = temp[i - 1];
		Point p2 = temp[i + 1];
		if (a*p.x + b*p.y + c <= 0)
		{
			temp_temp[++cut_num] = p;
		}
		else
		{
			if (a*p1.x + b*p1.y + c < 0)
			{
				temp_temp[++cut_num] = intersect(temp[i - 1], temp[i]);
			}
			if (a*p2.x + b*p2.y + c < 0)
			{
				temp_temp[++cut_num] = intersect(temp[i], temp[i + 1]);
			}
		}
	}
	for (int i = 1; i <= cut_num; i++)
	{
		temp[i] = temp_temp[i];
	}
	temp[cut_num + 1] = temp_temp[1];
	temp[0] = temp_temp[cut_num];
	num_temp = cut_num;
}
double solve()
{
	double l = 0, r = 1000000;
	double mid;
	while (r - l >= 1e-5)
	{
		mid = (l + r) / 2;
		for (int i = 0; i <= n + 1; i++)
		{
			temp[i] = point[i];
		}
		num_temp = n;
		for (int i = 1; i <= n; i++)
		{
			getline(point[i], point[i + 1]);
			c += mid * sqrt(a*a + b*b);
			cut();
		}
		if (num_temp)
			l = mid;
		else
			r = mid;
	}
	return r;
}
int main()
{
	int t;
#ifdef glx
	freopen("in.txt", "r", stdin);
#endif
	while (~scanf("%d", &n)&&n)
	{
		for (int i = 1; i <= n; i++)
		{
			scanf("%lf%lf", &point[i].x, &point[i].y);
		}
		point[0] = point[n];
		point[n + 1] = point[1];
		printf("%.6lf\n", solve());
		//cout << num_temp << endl;
	}
	return 0;
}