题目:
Suppose that we wish to keep track of a point of maximum overlap in a set of intervals—a point that has the largest number of intervals in the database overlapping it.
a.略
b.Keep a balanced binary tree of the endpoints. That is, to insert an interval,we insert its endpoints separately. With each left endpoint e, associate a valuep[e] = +1 (increasing the overlap by 1). With each right endpoint e associate a value p[e] = −1 (decreasing the overlap by 1). When multiple endpoints have the same value, insert all the left endpoints with that value before inserting anyof the right endpoints with that value.
这道题花了我很久的时间,一方面由于自己当初思路有误,另一方面我认为网上能够找到的有用的资料有限,所以我想把这道题写清楚,以供后来的同学参考学习,如果有想交流的可以联系我邮箱(博客上有)。
这是introductor_s Manual for CLRS上的思路。(后面有我的理解与阐述)
Keep a balanced binary tree of the endpoints. That is, to insert an interval,we insert its endpoints separately. With each left endpoint e, associate a value p[e] = +1 (increasing the overlap by 1). With each right endpoint e associate a value p[e] = −1 (decreasing the overlap by 1). When multiple endpoints have the same value, insert all the left endpoints with that value before inserting any of the right endpoints with that value.Here’s some intuition. Let e 1 , e 2 , . . . , e n be the sorted sequence of endpoints corresponding to our intervals. Let s(i, j ) denote the sum p[e i ] + p[e i+1 ] + · · · + p[e j ] for 1 ≤ i ≤ j ≤ n. We wish to find an i maximizing s(1, i). Each node x stores three new attributes. Suppose that the subtree rooted at x includes the endpoints e l[x] , . . . , e r[x] . We store v[x] = s(l[x], r[x]), the sum of the values of all nodes in x’s subtree. We also store m[x], the maximum value14-16 Solutions for Chapter 14: Augmenting Data Structures obtained by the expression s(l[x], i) for any i in {l[x], l[x] + 1, . . . , r[x]}. Finally, we store o[x] as the value of i for which m[x] achieves its maximum. For the sentinel, we deÞne v[nil[T ]] = m[nil[T ]] = 0.We can compute these ttributes in a bottom-up fashion to satisfy the requirements of Theorem 14.1:
v[x] = v[left[x]] + p[x] + v[right[x]] ,
m[left[x]](max is in x’s left subtree)
m[x] = max v[left[x]] + p[x](max is at x) ,
v[left[x]] + p[x] + m[right[x]] (max is in x’s right subtree) .The computation of v[x] is straightforward. The computation of m[x] bears further explanation. Recall that it is the maximum value of the sum of the p values for the nodes in x’s subtree, starting at l[x], which is the leftmost endpoint in x’s subtree and ending at any node i in x’s subtree. The value of i that maximizes this sum is either a node in x’s left subtree, x itself, or a node in x’s right subtree. If i is a node in x’s left subtree, then m[left[x]]
represents a sum starting at l[x], and hence m[x] = m[left[x]]. If i is x itself, then m[x] represents the sum of all p values in x’s left subtree plus p[x], so that m[x] = v[left[x]] + p[x]. Finally, if i is in x’s right subtree, then m[x] represents the sum of all p values in x’s left subtree, plus p[x], plus the sum of some set of p values in x’s right subtree. Moreover, the values taken from x’s right subtree must start from the leftmost endpoint in the right subtree. To maximize this sum, we need to maximize the sum from the right subtree, and that value is precisely m[right[x]]. Hence, in this case, m[x] = v[left[x]] + p[x] + m[right[x]]. Once we understand how to compute m[x], it is straightforward to compute o[x] from the information in x and its two children. Thus, we can implement the operations as follows:
I NTERVAL -I NSERT : insert two nodes, one for each endpoint of the interval.
I NTERVAL -D ELETE : delete the two nodes representing the interval end-points.
F IND -POM: return the interval whose endpoint is represented by o[root[T ]].Because of how we have deÞned the new attributes, Theorem 14.1 says that each operation runs in O(lg n) time. In fact, F IND -POM takes only O(1) time.
下面我用到的m,p,v都与上面定义的含义相同。
思路如下:
1.给定n/2个区间,那么从小到大有n个端点,将这n个端点从小到大排列起来,那么最大重叠点对就的就是使p[e1] + p[e 2 ] + · · · + p[e i]这个式子取得最大值的点,这个相对来说比较好理解,如果前面的区间只出现了左端点,还没有出现右端点,那么肯定会与当前这个区间重叠。如果左右端点都出现过了,那么也就不会与当前区间重叠了,同时左端点p为+1,右端点p为-1,相加为0。有了这个式子,就非常有效的把求最大重叠点的这个问题抽象化了,转换为了如何求这个式子的最大值。我之前就一直没看懂上面的那个max式子,自己开始想各种区间相互重叠的情况,试图分析各种情况找到规律(然而并没有什么用,费了很多时间)。
2.光知道1中这个式子也没有用,现在的关键是如何去计算这个式子的最大值。方法就是算法导论前面讲过的分治。所有端点有序排列,当一个端点(设为i)把区间分成了左右两部分和端点i自身,而且知道了1,2,3,....i-1这i-1个点的最大重叠点(设为i->left->m),以及i+1,i+2,...n这n-i个点的最大重叠点(设为i->right->m)。这个时候整个区间的最大重叠点(对应的重叠次数设为m)所处位置分成了三种情况:
a:在i的左边 m1 = i->left->m;
b:就是i本身 m2 = i->left->v (i左边区间的所有端点的p值之和)+ i->p;
c:在i的右边 m3 = i->left->v (i左边区间的所有端点的p值之和)+ i->p +i->right->m ;
所以m = max(m1,m2,m3).
由此这个求当前区间最大重叠点的问题转化为了两个求更小区间最大重叠点的子问题。
3.红黑树正好能提供这种功能,一颗树的根以及其左右子树相应的将区间分成三个部分。比如说我设计了以下几个区间:
[1,2] [3,5],[4,6],[5,7],[8,9](观察可知最大重叠点为5,m=3)
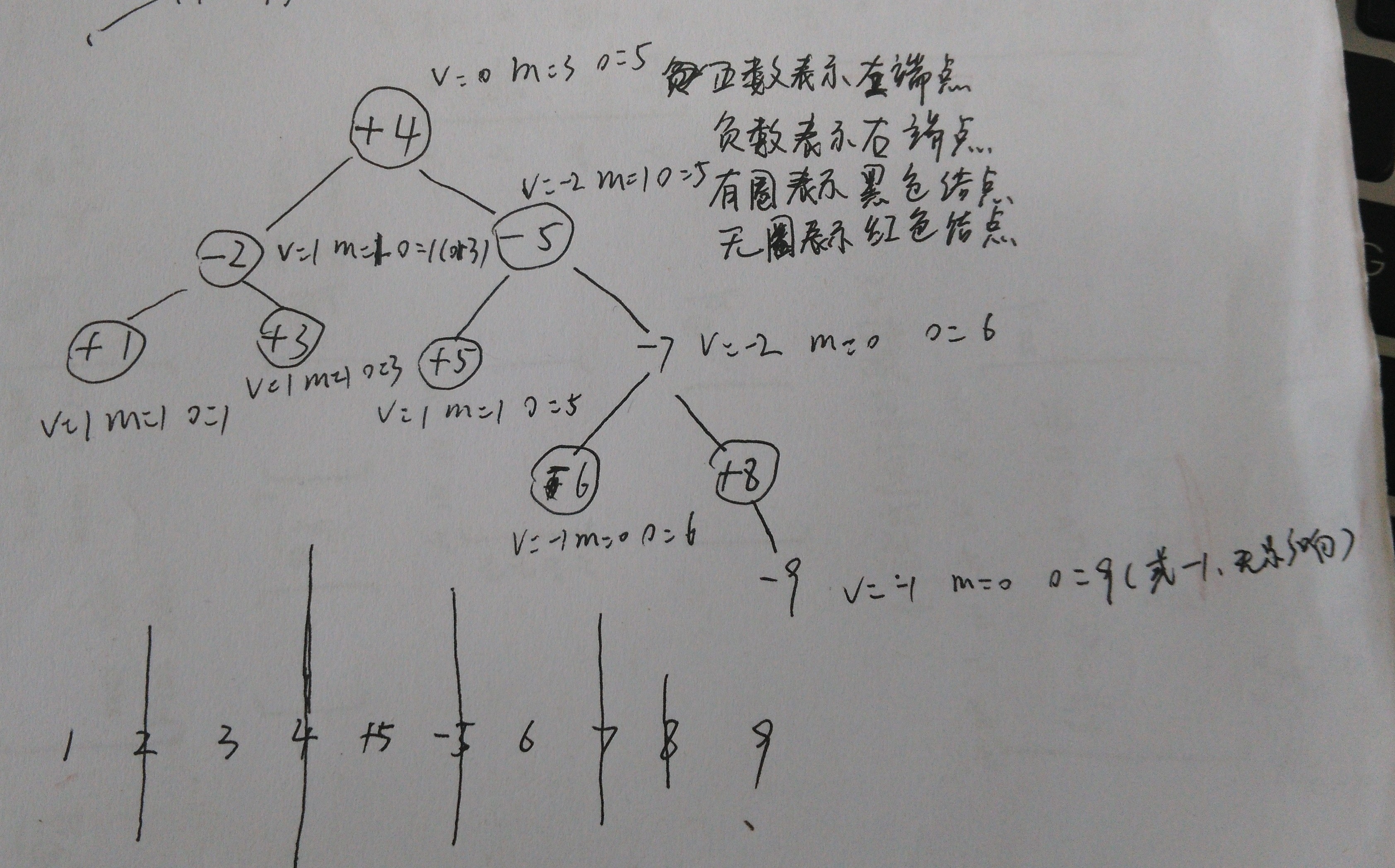
将各端点从小到大(相同的值左端点插入完了之后再插入右端点)生成了如下一颗红黑树,对应的将区间分成了连续的小块:
从叶子结点不断向上,区间不断合并,最终组成了整个区间,也就得到了最终的答案。如果插入或者删除某个元素,只需要重新维护其到根结点的路径上的所有的点的信息即可,时间复杂度为o(lgn);
4.完善了所有附加属性的完整的树如下:
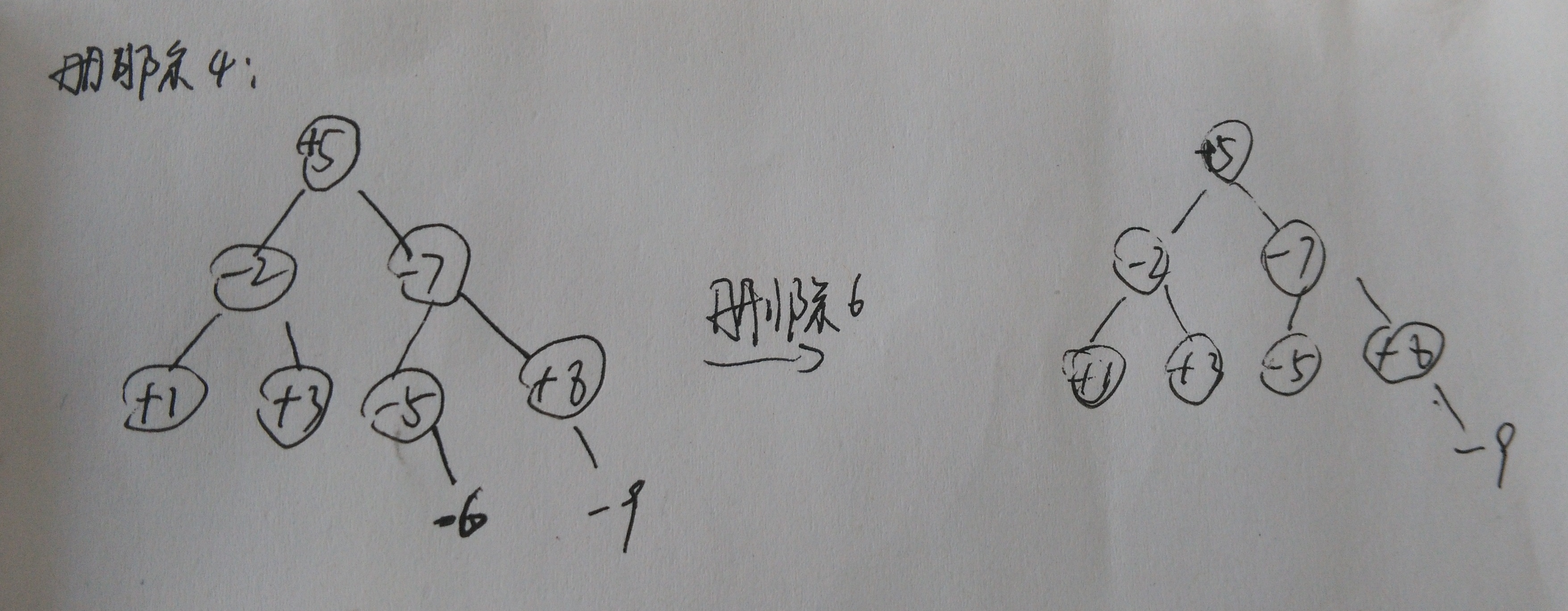
5.删除节点测试。删除[4,6]区间。
得到的树如下:
代码如下(如有错误,欢迎指正):
#include "StdAfx.h"
#include <iostream>
using namespace std;
#define BLACK 0
#define RED 1
typedef struct Node
{
int key;
Node* parent;
Node* left;
Node* right;
bool color;
//扩展属性
int v;
int p;
int m;
int o;
Node(Node*init,int key)
:key(key),left(init),right(init),parent(init),color(RED),v(0),m(0),o(key){}
//初始颜色设为红色 因为新插入的结点颜色为红色
//所以说nil结点需要再手动将颜色设置为黑色
};
typedef struct Red_Black_Tree
{
Node* root;
Node* nil;
Red_Black_Tree()
{
nil = new Node(NULL,-1);
nil->color = BLACK;//nil结点颜色为黑色
root = nil;
}
};
int max(int a,int b,int c)
{
a = a > b?a:b;
return a > c?a:c;
}
//最大重叠点的维护
void maintain_maxOverlap_toRoot(Red_Black_Tree* T,Node*z)
{
while(z != T->nil)
{
z->v = z->left->v + z->p + z->right->v;
z->m = max(z->left->m,
z->left->v+z->p,
z->left->v+z->p+z->right->m);
if(z->m == z->left->m)
z->o = z->left->o;
else if(z->m == z->left->v+z->p)
z->o = z->key;
else
z->o = z->right->o;
z = z->parent;
}
}
//对于旋转来说 只有两个节点需要重新维护
void maintain_maxOverlap_oneNode(Red_Black_Tree* T,Node*z)
{
z->v = z->left->v + z->p + z->right->v;
z->m = max(z->left->m,
z->left->v+z->p,
z->left->v+z->p+z->right->m);
if(z->m == z->left->m)
z->o = z->left->o;
else if(z->m == z->left->v+z->p)
z->o = z->key;
else
z->o = z->right->o;
z = z->parent;
}
//左旋 完全参照教材算法导论中文版第三版p177
void left_rotate(Red_Black_Tree* T,Node* x)
{
Node* y = x->right;
x->right = y->left;
if(y->left != T->nil)
y->left->parent = x;
y->parent = x->parent;
if(x->parent == T->nil)
T->root = y;
else if(x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
maintain_maxOverlap_oneNode(T,x);
maintain_maxOverlap_oneNode(T,y);
}
void right_rotate(Red_Black_Tree* T,Node* x)
{
Node* y = x->left;
x->left = y->right;
if(y->right != T->nil)
y->right->parent = x;
y->parent = x->parent;
if(x->parent == T->nil)
T->root = y;
else if(x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->right = x;
x->parent = y;
maintain_maxOverlap_oneNode(T,x);
maintain_maxOverlap_oneNode(T,y);
}
void rb_insert_fixup(Red_Black_Tree* T,Node* z)
{
while(z->parent->color == RED)
{
if(z->parent == z->parent->parent->left)
{
Node* y = z->parent->parent->right;
//case1
if(y->color == RED)
{
z->parent->color = BLACK;
y->parent->color = BLACK;
y->parent->parent->color = RED;
z = y->parent->parent;
}
else
{
//case2
if(z == z->parent->right)
{
z = z->parent;
left_rotate(T,z);
}
//case3
z->parent->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
right_rotate(T,z);
z = T->root;
}
}
else//z->parent == z->parent->parent->right
{
Node* y = z->parent->parent->left;
//case1
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
//case2
if(z == z->parent->left)
{
z = z->parent;
right_rotate(T,z);
}
//case3
z->parent->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
left_rotate(T,z);
}
}
}
T->root->color = BLACK;
}
void rb_insert(Red_Black_Tree* T,Node* z)
{
Node* y = T->nil;
Node* x = T->root;
while(x != T->nil)
{
y = x;
if(z->key < x->key)
x = x->left;
else
x = x->right;
}
if(y == T->nil)
T->root = z;
else if(z->key < y->key)
y->left = z;
else
y->right = z;
z->parent = y;
maintain_maxOverlap_toRoot(T,z);//通过实验与思考发现 由于对于旋转操作来说 先调整颜色 或者先维护信息都可以(后面删除的情况也一样)
// 但是我觉得这有一定碰巧的因素在里面 先维护信息(使整颗树的信息正确),然后fixup(插入和删除)在变换过程中也维护这种
//信息不变 在逻辑上更严密 也更容易理解
rb_insert_fixup(T,z);
//maintain_maxOverlap_toRoot(T,z);
}
//返回以z为根结点的子树中的最小元素
Node* tree_min(Red_Black_Tree* T, Node* z)
{
while(z->left != T->nil)
z = z->left;
return z;
}
// //返回结点的后继
// Node* tree_sucessor(Red_Black_Tree* T,Node* z)
// {
// if(z->right != T->nil)
// return tree_min(T,z->right);
// else
// {
// while(z == z->parent->right)
// z = z->parent;
// return z;
// }
// }
//让v结点替代u结点与u结点的父节点互相连接
void tree_node_replace(Red_Black_Tree*T, Node* u,Node* v)
{
v->parent = u->parent;
if(u->parent == T->nil)
T->root = v;
else if(u == u->parent->left)
u->parent->left = v;
else
u->parent->right = v;
}
void rb_delete_fixup(Red_Black_Tree* T,Node* x)
{
while(x != T->root && x->color == BLACK)
{
if(x == x->parent->left)
{
Node* w = x->parent->right;
//case1
if(w->color == RED)
{
w->color = BLACK;
x->parent->color = RED;
left_rotate(T,x->parent);
}
//case2
else if(w->left->color == BLACK && w->right->color == BLACK)
{
w->color = RED;
x = x->parent;
}
else
{
//case3
if(w->left->color == RED)
{
w->color = RED;
w->left->color = BLACK;
right_rotate(T,w);
w = x->parent->right;
}
//case4
w->right->color = BLACK;
w->color = x->parent->color;
x->parent->color = BLACK;
left_rotate(T,x->parent);
x = T->root;
}
}
else//x == x->parent->right
{
Node* w = x->parent->left;
//case1
if(w->color == RED)
{
w->color = BLACK;
x->parent->color = RED;
right_rotate(T,x->parent);
}
//case2
else if(w->left->color == BLACK && w->right->color == BLACK)
{
w->color = RED;
x = x->parent;
}
else
{
//case3
if(w->right->color == RED)
{
w->color = RED;
w->right->color = BLACK;
left_rotate(T,w);
w = x->parent->left;
}
//case4
w->left->color = BLACK;
w->color = x->parent->color;
x->parent->color = BLACK;
right_rotate(T,x->parent);
x = T->root;
}
}
}
x->color = BLACK;
}
void rb_delete(Red_Black_Tree* T,Node*z)
{
bool original_color = z->color;//用来记录被删除的节点的颜色
Node* x;//用来记录可能引起红黑树性质被破坏的点
if(z->left == T->nil)
{
tree_node_replace(T,z,z->right);
x = z->right;
}
else if(z->right == T->nil)
{
tree_node_replace(T,z,z->left);
x = z->left;
}
else
{
Node* y = tree_min(T,z->right);
if(y != z->right)
{
original_color = y->color;
tree_node_replace(T,y,y->right);//y->left 一定为nil
x = y->right;
y->right = z->right;
z->right->parent = y;
}
tree_node_replace(T,z,y);
y->color = z->color;
y->left = z->left;//因为有了nil这个哨兵 所以无需再进行判断
z->left->parent = y;
}
maintain_maxOverlap_toRoot(T,x->parent);
if(original_color == BLACK)
rb_delete_fixup(T,x);
//maintain_maxOverlap_toRoot(T,x->parent);
}
//求最大覆盖点
int find_pom(Red_Black_Tree *T)
{
return T->root->o;
}
Node* tree_search(Red_Black_Tree* T,int key)
{
Node* z = T->root;
while(z != T->nil)
{
if(z->key == key)
return z;
else if(key < z->key)
z = z->left;
else
z = z->right;
}
return T->nil;
}
//插入的区间为[1,2] [3,5],[4,6],[5,7],[8,9]
//观察可知5为最大重叠点 与程序所求吻合
int main()
{
int a[][2] = {{1,1},{2,-1},{3,1},{4,1},{5,1},{5,-1},{6,-1},{7,-1},{8,1},{9,-1}};
Red_Black_Tree* Tree = new Red_Black_Tree;
for(int i=0;i<10;i++)
{
Node* node = new Node(Tree->nil,a[i][0]);
node->p = a[i][1];
rb_insert(Tree,node);
}
cout<<"最大重叠点:"<<find_pom(Tree)<<endl;
cout<<"重叠次数:"<<Tree->root->m<<endl;
//删除[4,6]区间
Node* node = tree_search(Tree,4);
rb_delete(Tree,node);
node = tree_search(Tree,6);
rb_delete(Tree,node);
cout<<"最大重叠点:"<<find_pom(Tree)<<endl;
cout<<"重叠次数:"<<Tree->root->m<<endl;
return 0;
}
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








