欧拉公式：零基础图解欧拉公式推导，小学二年级适用

欧拉公式的数形结合理解

1. 引言

• 在B站上看到一个极好的证明欧拉公式的视频，推荐给大家，并写文章记录下自己的理解

https://www.bilibili.com/video/av301216122/?vd_source=1db9625b9b10dd5c0b79fbe79e3b9a91
数学上有句话，当一个公式中出现π时，一定要问自己那个圆在哪里？

• “上帝公式”用极简的符号编织出深邃的关联。当指数函数e^(iθ)引入了iθ的调和，它不再是爆炸的增长曲线，而是化作单位圆上轻盈的旋转。这个等式最震撼的瞬间，是当θ=π时所有元素骤然收紧：自然常数e与圆周率π在复平面上相遇，旋转半周后精准地跌入-1的谷底，而一个朴素的"+1"便将万物归为虚无。数学中的五大神明——0和1构筑算术，i定义虚数，π丈量圆，e刻画自然增长——竟在此处完美画上等号！

• 它撕开了不同领域的藩篱。指数的导数特性、复数的几何意义、三角函数的周期性，都在此达成共识。工程师用它解微分方程，物理学家用它描述波动，而每一个凝视公式的人，都能在抽象符号的共振中触碰到数学的统一性。这种美不依赖修辞堆砌，而是源自逻辑本身的清澈回响。

• 上学的时候被各种知识轰炸，那会儿实在没有欣赏到欧拉公式的美，直到工作后重新学信号处理终于有所感悟，欧拉公式确实美的难以言表，但我词穷只会说卧槽，遂只好用AI帮我表达，希望读者也能感受到上帝公式的美。

2. 正文

1. 欧拉公式： $$e^{i\pi }+1=0$$

2. 可以借助e的定义进行证明：$$e=\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n$$
   视频在给出e的定义时顺带给出了该极限形式的意义，就是计算存款利率收益，假设银行一年结算一次收益为(1+r)，一年结算两次收益为(1+r/2)^2，当结算次数趋于无穷时极限就收敛于e^r。$$e^r=\underset{n\to \infty }{\lim }(1+\frac{r}{n}{)}^n$$

3. 那么我们就可以借助e的极限定义来推导e^ipi，$$e^{i\pi }=\underset{n\to \infty }{\lim }(1+\frac{i\pi }{n}{)}^n=？$$此时，式中涉及到了复数的乘法，即$$(a+bi)(c+di)=(ac-ad)+(bd+bc)i$$
   但如果用这个公式来推导显然有点摸不到头脑了，而且我们是寻求一种数形结合的直观理解，所以我们需要的其实是复数的三角表示，即$$(a(cos\alpha +isin\alpha ))(b(cos\beta +isin\beta ))=ab(cos(\alpha +\beta )+isin(\alpha +\beta ))$$
   其几何意义就是复数的乘积等于辐角相加模相乘。

4. 重新回到欧拉公式的推导，我们可以依次画出n=1、n=2、n=3…时的图像，
   
   
   
   
   
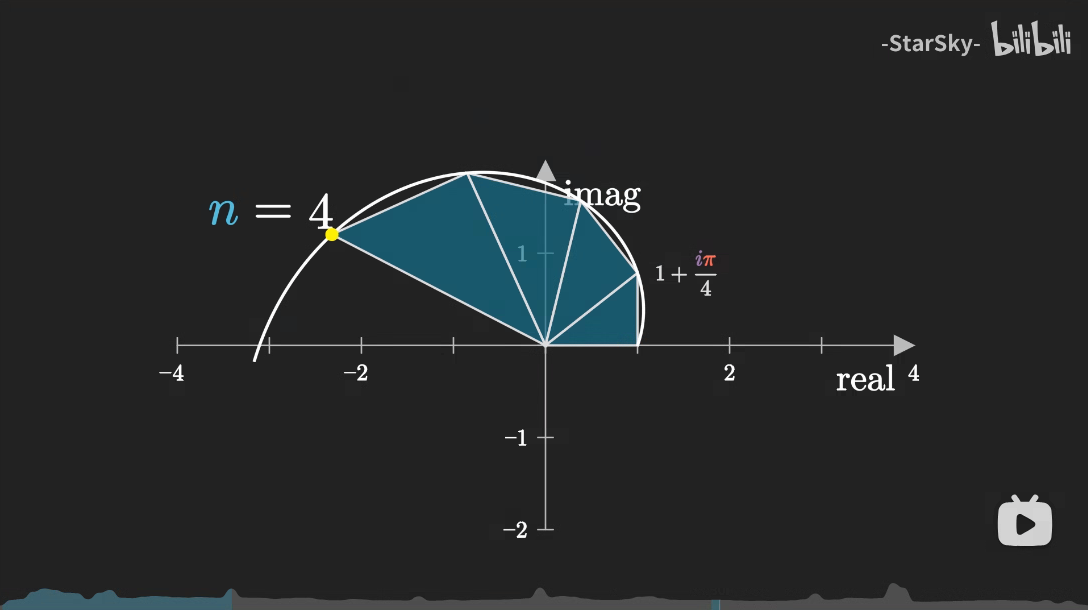
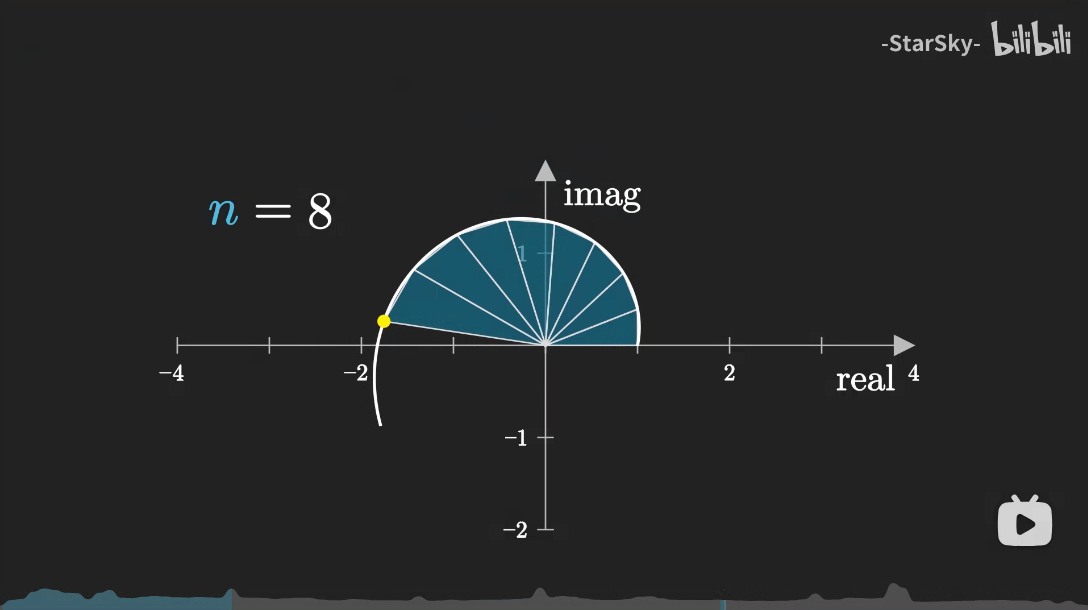
   宏观上看就是矢量(1,0)不断地乘(1,iπ/n)最终画了一个圆指向了(-1,0)，当然这样子画还不能“显然”，但当我们细看每次变化时，这个结果就是传说中的“显然”了，
   
   当n较小时，矢量(1,iπ/n)的模较大，那么矢量(1,iπ/n)相乘后的模也较大，方向是逆时针旋转，从图像看就是三角形的斜边明显大于直角边
   
   但当n较大时，矢量(1,iπ/n)的模较小，那么矢量(1,iπ/n)相乘后的模就比n较小时小，换句话就说就是每乘上一个(1,iπ/n)后几乎不改变原来的模长，而只有旋转的效果，从图像上看就是三角形的斜边越来越接近直角边。
   那么，当n->无穷时，每一个矢量(1,iπ/n)相乘的贡献就只有旋转一个极小度数的作用，而并不改变模长，这个角度为π/n（θ无穷小时tan(θ)≈θ），从图像上看就是三角形变成了扇形，而最终的结果就是矢量(1,0)旋转到了(-1,0)。

   n = 0:100;
   result = (1+1i*pi./n).^n;
   figure(1),scatter(real(result),imag(result));
   axis([-4 4 -4 4])
   grid on
   
   N = 100;
   process = nan(1,N);
   process(1) = 1;
   for i = 2:N
       process(i) = process(i-1)*(1+1i*pi./(N-1));
   end
   figure(2),scatter(real(process),imag(process));
   axis([-4 4 -4 4])
   grid on
   

   用matlab简单仿真看了看，加深印象
   
   
   
   

5. 视频中还给出一种方式去理解最终结果是-1，当n趋于无穷时，每个小三角形变成扇形，其弧长是π/n，半径是1（看第一个小三角，长边是(1,π/n)的实部1，短边是虚部π/n），n个小三角弧长就是π，利用弧长公式，那么这个圆弧就正好是个半圆，所以最终的结果就是-1。（这个理解也不错，但我觉得从矢量(1,iπ/n)相乘的几何意义去理解就已经非常“显然”了）
   
   每一个小三角形的短边长度是π/n

6. 关于无穷个矢量(1,iπ/n)相乘的贡献并不改变模长，这句话是成立的，视频里也给出了证明，但我高数学得不咋滴没看懂哈哈。
   

7. 推广一下，当π为任意角度θ时，每一个矢量(1,iθ/n)相乘的贡献为将矢量(1,0)旋转θ/n，而并不改变模长，即$$e^{i\theta }=cos\theta +isin\theta$$

8. 再推广一下，θ换成频率乘时间，信号处理的篇章就此展开。