【随缘一练】找出abb型字符串的个数

博主未授权任何人或组织机构转载博主任何原创文章，感谢各位对原创的支持！
博主链接

题目

描述
leafee 最近爱上了 abb 型语句，比如“叠词词”、“恶心心”
leafee 拿到了一个只含有小写字母的字符串，她想知道有多少个 “abb” 型的子序列？
定义： abb 型字符串满足以下条件：

• 字符串长度为 3 。
• 字符串后两位相同。
• 字符串前两位不同。

输入描述：
第一行一个正整数 n
第二行一个长度为 n 的字符串（只包含小写字母）
1 <= n <= 10⁵

输出描述：
“abb” 型的子序列个数。
示例1

输入：
6
abcbcc

输出：
8
说明：
共有1个abb，3个acc，4个bcc

示例2

输入：
4
abbb

输出：
3

思路一：三个for循环搞定，但是提示超时

第一个for选择abb字符串中的第一个字符，然后第二个for确定第二个字符，同理第三个for确定最后一个字符。
这个时间复杂度就不说了O(n³)，空间复杂度O(1)

#include<stdio.h>

int main()
{
    int n,res=0;
    scanf("%d",&n);
    getchar();
    char *s=(char*)malloc(n+1);
    gets(s);
    
    for(int i=0;i<n;++i)
    {
        for(int j=i+1;j<n;++j)
        {
            if(s[i]!=s[j])
            {
                for(int k=j+1;k<n;++k)
                {
                    if(s[j]==s[k])
                        res++;
                }
            }
        }
    }
    printf("%d",res);
    
    return 0;
}

思路二：动态规划

使用dp[i][26] （i从0开始）记录 [i+1,n-1] 之间每个字母出现的次数，之后我们利用数学中的排列$$C_n^2=n\ast (n-1)/2!$$计算出以s[i]开头的abb字符串的个数

#include<stdio.h>

int main()
{
    long long n,res=0;
    scanf("%lld",&n);
    getchar();
    char *s=(char*)malloc(n+2);
    long long (*dp)[26]=(long long*)malloc(sizeof(long long)*(n+2)*26);
    memset(dp,0,sizeof(long long)*(n+2)*26);
    gets(s);
    
    for(int i=n-1;i>=0;--i)
    {
        for(int j=0;j<26;++j)
            dp[i][j] = dp[i+1][j];
        ++dp[i][s[i]-'a'];
    }
    
    for(int i=0;i<n;++i)
    {
        for(int j=0;j<26;++j)
        {
            if(s[i]-'a' != j)
            {
                res += dp[i+1][j]*(dp[i+1][j]-1)/2;
            }
        }
    }
    printf("%lld",res);
    
    return 0;
}

时间复杂度O(n)，空间复杂度O(n)

思路三：动态规划优化

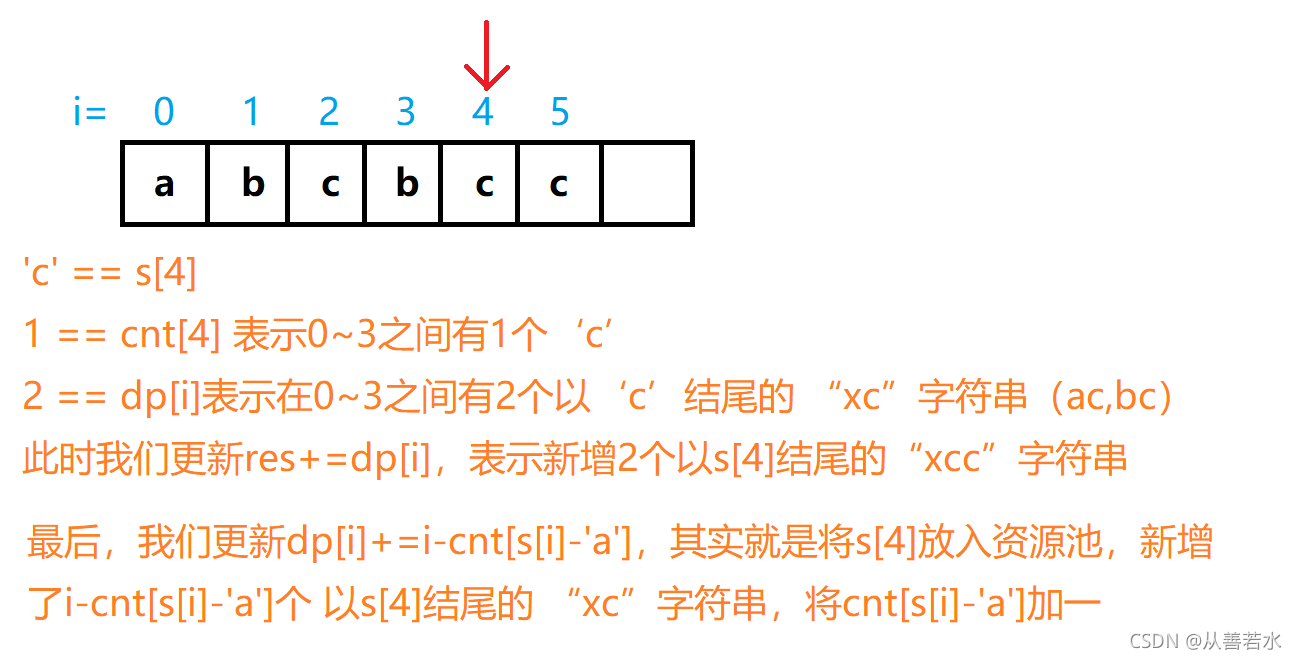
#include<stdio.h>

int main()
{
    long long n,res=0;
    long long cnt[26]={0},dp[26]={0};
    scanf("%lld",&n);
    getchar();
    char *s=(char*)malloc(n+1);
    gets(s);
    
    for(int i=0;i<n;++i)
    {
        res+=dp[s[i]-'a'];
        dp[s[i]-'a']+=i-cnt[s[i]-'a'];
        ++cnt[s[i]-'a'];
    }
    
    printf("%lld",res);
    free(s);
    return 0;
}

时间复杂度O(n)，空间复杂度O(1)

---

这里是从善若水的博客，感谢您的阅读💯💯💯

---