首先,Lucas(卢卡斯)定理是什么?有什么用?
Lucas定理是用来求 C(n,m) mod p,p为素数 的值 。(注意:p一定是素数)
有人会想,C(n,m)不能用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式来递推吗?
( 提示:C(n, m) mod p = n!/(m!(n - m)!) mod p )
可以是可以。但当n,m,p都很大时,你递推所用的时间就会很爆炸了。所以,这就需要用到Lucas定理来解决了。
因此,Lucas定理用来解决 大组合数求模 是很有用的 。
注意: Lucas定理最大的数据处理能力是p在10^5左右,不能再大了。再大的话,也是可以求的
表达式:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p。(可以递归)
递归方程:(C(n%p, m%p)*Lucas(n/p, m/p))%p。(递归出口为m==0,return 1)
-----------------------------------------------------------------------
Lucas定理 定义 : :
这里我们令 n=sp+q , m=tp+r . (q ,r ≤p)
那么:
( 在编程时你只要继续对
调用Lucas定理即可。
)
( 代码可以递归的去完成这个过程,其中递归终点为
t = 0
)
(时间复杂度
O(logp (n)*p) :)
-------------------------------------------------------------------------------------------
Lucas定理
证明 :
首先你需要这个算式 :
,
其中f > 0&& f < p。
然后 (1 + x) n Ξ (1 + x) sp+q Ξ ( (1 + x)p )s · (1 + x) q Ξ (1 + xp ) s · (1 + x) q (mod p) 。
所以得 (1 + x) sp+q
我们求右边的 的系数为:
通过观察你会发现当且仅当i = t , j = r ,能够得到
的系数,及
。
所以,得证。
--------------------------------------------------------------------------------------------------
我再次将它公式化一下。
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base
p
expansions of
m
and
n
respectively.
已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然是除法取模,这里又要用到m!(n-m)!的逆元。
求逆元(此处不详细说明了(ˇˍˇ) )。。。
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 。
按照上面的思路就可以写出Lucas定理的代码了:
参考代码:
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N =1e5; ll n, m, p, fac[N]; void init() { int i; fac[0] =1; for (i =1; i <= n; i++) fac[i] = fac[i-1]*i % p; } ll q_pow(ll a, ll b) { ll ans =1; while (b) { if (b &1) ans = ans * a % p; b>>=1; a = a*a % p; } return ans; } ll C(ll n, ll m) { if (m > n) return 0; return fac[n]*q_pow(fac[m]*fac[n-m], p-2) % p; } ll Lucas(ll n, ll m ) { if (m ==0) return 1; else return (C(n%p, m%p)*Lucas(n/p, m/p))%p; } int main() { int t; scanf("%d" , &t); while (t--) { scanf("%I64d%I64d%I64d" , &n, &m, &p); init(); printf("%I64d\n" , Lucas(n, m)); } return 0; }
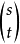
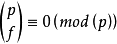 ,
其中f > 0&& f < p。
,
其中f > 0&& f < p。
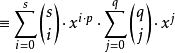
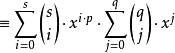
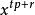
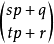
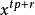
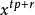 的系数,及
的系数,及
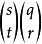 。
。
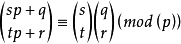 。得证。
。得证。
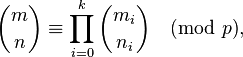
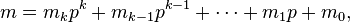
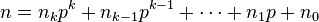







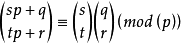














 1171
1171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








