题意:
给定长度为n的一个正整数序列,里面每个数的大小均为最大为m,让你构造出另一个等长的正整数序列要求满足一下三个条件:
1、数列里的每个数小于等于m。
2、整个数列的最大公因子为d。
3、你构造出的数列与原数列对应位置上的数刚好有k对不相等。
询问你当d 分别为 1~m 时,能构造出序列的种类数。
思路:
不好直接考虑计算最大公因子刚好为d的结果(设为f(d)),那么先计算最大公因子为d的倍数的结果(设为g(d)),那么可知,,其中u(i) 为反演系数,那么已知g函数的结果,我们就能在O(mlog(n))的时间求得答案。
条件三可以理解为从原数列中选k个数改变。
那么就有n-k个数的值不发生改变,如果这n-k个数中存在不是d的倍数的数,那么就无法得到要求的数列,此时结果为0。
设原数列中有x个数为d的倍数,那么:
① n-k > x :
说明不变的数中一定有数不是d的倍数,此时结果为0
g[d] = 0
② n-k <= x :
对于 (n-k) 个不是d的倍数的数 ,这些数一定要改变成小于等于m的d的倍数,它们有m/d中选择。
对于 剩下的 j = ( x - (n-k) )个原本就是d的倍数的数,这些数的选择有 C(x,j) 种,它们要变成除了它们自己以外的其余(m/d - 1)个数之一。
g[d] = pow(m/d , n-k ) * C(x,j) * pow(m/d -1 , j );
即可。
#include<bits/stdc++.h>
#define pii pair<int,int>
#define fi first
#define se second
const int mod = 1e9+7;
using namespace std;
int n,m,k;
int A[300005];
int mu[300005];
int pr[33000];
long long ni[300005];
long long fac[300006];
int isp[300005];
int num[300005];
long long ans[300005];
vector<pii>V;
vector<int>E[300005];
long long qpow(long long x,int y){
long long res = 1;
while(y){
if(y&1)res = res * x % mod;
y>>=1;
x = x * x % mod ;
}return res;
}
void init(){
fac[0] = ni[0] = 1;
for(int i=1;i<=3e5;i++){
isp[i]=true;
fac[i] =(1LL*fac[i-1]*i%mod);
ni[i] = qpow(fac[i],mod-2);
for(int j=i;j<=3e5;j+=i){
E[j].emplace_back(i);
}
}
mu[1]=1;
int all = 0;
for(int i=2;i<=3e5;i++){
if(isp[i]){
mu[i] = -1;
pr[all++] = i;
}for(int j=0;j<all;j++){
long long t = 1LL * pr[j] * i;
if(t>3e5)break;
mu[t] = -mu[i];
isp[t] = false;
if(i%pr[j]==0){
mu[t] = 0;
break;
}
}if(mu[i]){
V.emplace_back(pii(i,mu[i]));
}
}
}
inline long long C(int n,int m){
if(n==m||m==0)return 1LL;
return 1LL*fac[n]*ni[n-m]%mod*ni[m]%mod;
}
int main()
{
init();
while(scanf("%d%d%d",&n,&m,&k)==3){
memset(num,0,sizeof(num));
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
for(int j=0;j<E[A[i]].size();j++){
num[E[A[i]][j]]++;
}
}for(int i=1;i<=m;i++){
int cnt = m/i , j = k+num[i]-n;
if(n-num[i]<=k)ans[i] = 1LL * qpow(cnt,n-num[i]) * C(num[i],j) % mod * qpow(cnt-1,j) % mod;
else ans[i] = 0;
}for(int i=1;i<=m;i++){
for(int j=0;j<V.size();j++){
int t = V[j].fi * i ;
if(t<=m){
ans[i] = ( ans[i] + V[j].se * ans[t] + mod )% mod ;
}else {
break;
}
}printf("%I64d%c",ans[i],i<m?' ':'\n');
}
}return 0;
}








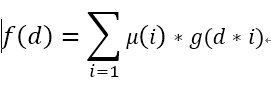














 357
357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








