2015年蓝桥杯省赛B组C/C++（试题+答案）前几题

一、奖券数目

有些人很迷信数字，比如带“4”的数字，认为和“死”谐音，就觉得不吉利。
虽然这些说法纯属无稽之谈，但有时还要迎合大众的需求。某抽奖活动的奖券号码是5位数（10000-99999），要求其中不要出现带“4”的号码，主办单位请你计算一下，如果任何两张奖券不重号，最多可发出奖券多少张。

请提交该数字（一个整数），不要写任何多余的内容或说明性文字。

简单数学问题
排列组合一下
8*9*9*9*9=52488

暴力搜索

#include <stdio.h>
int sum;
void dfs(int n)
{
    if(n>6) return ;
    if(n==6)
        sum++;
    for(int i=0;i<10;i++)
    {
        if(n==1&&i==0) continue;
        if(i==4) continue;
        dfs(n+1);
    }
}
int main()
{
     dfs(1);
     printf("\n%d\n",sum);
}

---

二、

星系炸弹

在X星系的广袤空间中漂浮着许多X星人造“炸弹”，用来作为宇宙中的路标。
每个炸弹都可以设定多少天之后爆炸。
比如：阿尔法炸弹2015年1月1日放置，定时为15天，则它在2015年1月16日爆炸。
有一个贝塔炸弹，2014年11月9日放置，定时为1000天，请你计算它爆炸的准确日期。

请填写该日期，格式为 yyyy-mm-dd 即4位年份2位月份2位日期。比如：2015-02-19
请严格按照格式书写。不能出现其它文字或符号。

本题最好还是用Excel
一来题目不难就是麻烦点
二来比赛时间有限啊
答案是 2017-08-05
要注意格式

---

三、三羊献瑞

观察下面的加法算式：

• 

其中，相同的汉字代表相同的数字，不同的汉字代表不同的数字。

请你填写“三羊献瑞”所代表的4位数字（答案唯一），不要填写任何多余内容。

这就是个数学题
先按数学题的方法解一下
语言表述的话很长 但思考的时候是很快的 如果没兴趣可以跳过
1，因为是加法算式三是进位出来的 所以是三是1
2，因为三是1且三加祥能进位，只有1+9能进位，所以祥是9
但是考虑可能有进位的情况祥可能为8或9 *
⑴，当祥为8时8+1+1（进位的1）=10 这时羊只能为0 而0+任何1~9数均<10 不可能进位 ——不成立
⑵，当祥为9时9+1+1（进位的1）=1，羊为1 因为三为1 所以羊不为1 ——不成立
综上得到三为1 祥为9 所以羊为0
3，瑞+0=生只能是后面进位了，得到瑞+1等于生。
又有生+献=瑞 即 瑞+1+献=瑞 即 1+献=0
（到这可能有些不明白，解释下，这又是因为后位进1导致1+献=0 应为 1+献+1（进位的1）=0 即献=8）
此时设瑞=x，辉=y，气=z。
这时所有的数的关系如下

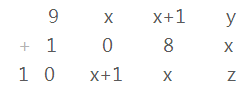
这时从x开始试数，1,0已经有了 从2开始试数
x=2时 x+y>=10，y>=8 而8,9已经存在—— 不成立
x=3时 x+y>=10，y>=7 8,9已经存在 也只能为7，但 x+y=3+7+10 z应为0 因0已经存在—— 不成立
x=4时 x+y>=10，y>=6 8,9已经存在 y可为6,7 当为6时z=0—— 不成立 当为7时 z=1 不成立
x=5时 x+y>=10，y>=5 8,9已经存在 y为7时 z为2 此时总式成立

所以得出结果为 9567+1085=10652

得出三样献瑞 为1085
此题目用推理的方式做出来 上述只是他的证明过程 所以文字多 篇幅长 但是这都是思考出来的 在实际操作中很快就会得出结果 比写暴力的代码要省时的多 毕竟代码那么多的for语句 还有那么多数字加在一起 很容易出错了 虽然不用代码 有点违背蓝桥杯是C++比赛的事实 但是做出题来得分 取得名次 才是王道

下面是常规暴力做法

#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
    int a, b, c, d, e, f, g;
    for(a = 1; a <= 9; a++)
    {
        for(b = 0; b <= 9; b++)
        {
            for(c = 0; c <= 9; c++)
            {
                for(d = 0; d <= 9; d++)
                {
                        for(e = 0; e <= 9; e++)
                        {
                            for(f = 0; f <= 9; f++)
                            {
                                for(g = 0; g <= 9; g++)
                                {
                                        if((a * 1000 + b * 100 + c * 10 + d) + (1000 + e * 100 + f * 10 + b) == (10000 + e * 1000 + c * 100 + b * 10 + g))
                                        {
                                            if(a != 1 && b != 1 && c != 1 && d != 1 && e != 1 && f != 1)
                                            {
                                                    if(a != b && a != c && a != d && a !=e && a != f && a != g && b != c && b != d && b != e && b != f && b != g && c != d && c != e && c != f && c != g && d != e && d != f && d != g && e != f && e != g && f != g)
                                                    {
                                                            cout<<1 * 1000 + e * 100 + f * 10 + b<<endl;
                                                    }

                                            }
                                        }

                                }
                            }
                        }

                }
            }
        }
    }
    return 0;
}

这么繁杂的代码 写起来也很影响心情啊
———————————Update—————————–
其实C++ 库中有一种函数是next_permutation()
它能够将序列的全排列全部计算出来,这样的话,这道题目的代码量就会减少太多了.
以下代码已经确认 ‘三’=1 ,‘祥’=9

bool check(int *a){
    return ((9*1000+a[0]*100+a[1]*10+a[2])+(1000+a[3]*100+a[4]*10+a[0])==(10000+a[3]*1000+a[1]*100+a[0]*10+a[5]));
}
int main(){
    int a[]={0,2,3,4,5,6,7,8};
    int tem = 8*7*6*5*4*3*2*1;
    while(tem--){
        if(check(a)){
            printf("%d\n",(1000+a[3]*100+a[4]*10+a[0]));
        }
        next_permutation(a,a+8);
    }
    return 0;
}

---

第6题：加号改乘号

题目大意

　　把1+2+3+…+48+49中的两个加号改成乘号（修改位置不能相邻），使得式子的结果由1225变为2015。

解题分析：

用双循环暴力两个乘号的位置，计算在数字i、j后的加号改为乘号，式子数值的变化即可，注意j的起始位置为i+2。

简化一下能得到是判断式为792=i*(i-1)+j*(j-1)

代码：

#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
    for(int i = 1; i <= 48; i++)
    {
        for(int j = i + 2; j <= 48; j++)
        {
            if(792==i*(i-1)+j*(j-1))
                cout<<i<<j<<endl;
        }

    }
    return 0;
}

---

7题：牌型种数

题目大意

原题：

小明被劫持到X赌城，被迫与其他3人玩牌。
一副扑克牌（去掉大小王牌，共52张），均匀发给4个人，每个人13张。
这时，小明脑子里突然冒出一个问题：
如果不考虑花色，只考虑点数，也不考虑自己得到的牌的先后顺序，自己手里能拿到的初始牌型组合一共有多少种呢？

请填写该整数，不要填写任何多余的内容或说明文字。

解题分析：
这里也是两种方法， 暴力搜索。

题目很容易 记住剪枝 能快不少

#include <iostream>
#include <stdio.h>
using namespace std;
__int64 sum=0;
void dfs(int x,int num)
{
    if(num>13) return;
    if(x==0)
    {
        if(num==13)
            sum++;
        return;
    }
    for(int i=0; i<5; i++)
    {
        dfs(x-1,num+i);
    }
}
int main()
{
    dfs(13,0);
    printf("%I64d\n",sum);
    return 0;
}

---

就这么多吧