关于最小生成树与Kruskal算法、Prim算法的概念这位算法导论--最小生成树(Kruskal和Prim算法)已经写得很好了,这里我直接转载过来,就不赘述了。
关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vi与vj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vi与vj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
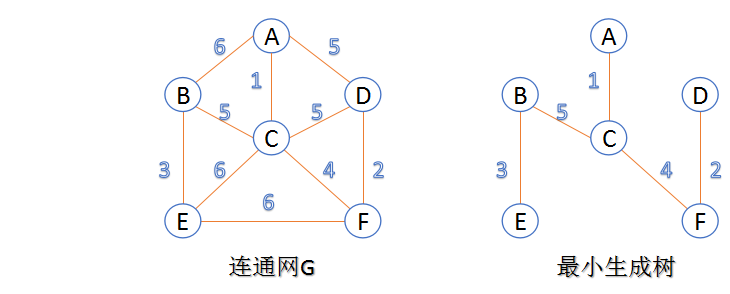
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
下面介绍两种求最小生成树算法
1.Kruskal算法
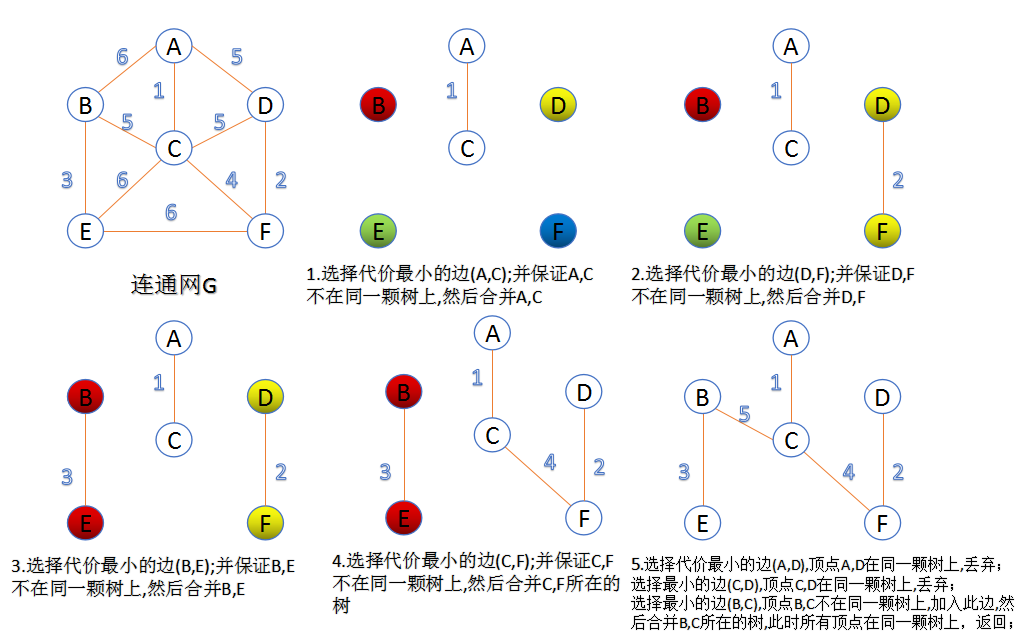
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。该算法以边为主 适用于边多点少的图形中 。
1. 把图中的所有边按代价从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大选择边,所选的边连接的两个顶点ui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
2.Prim算法
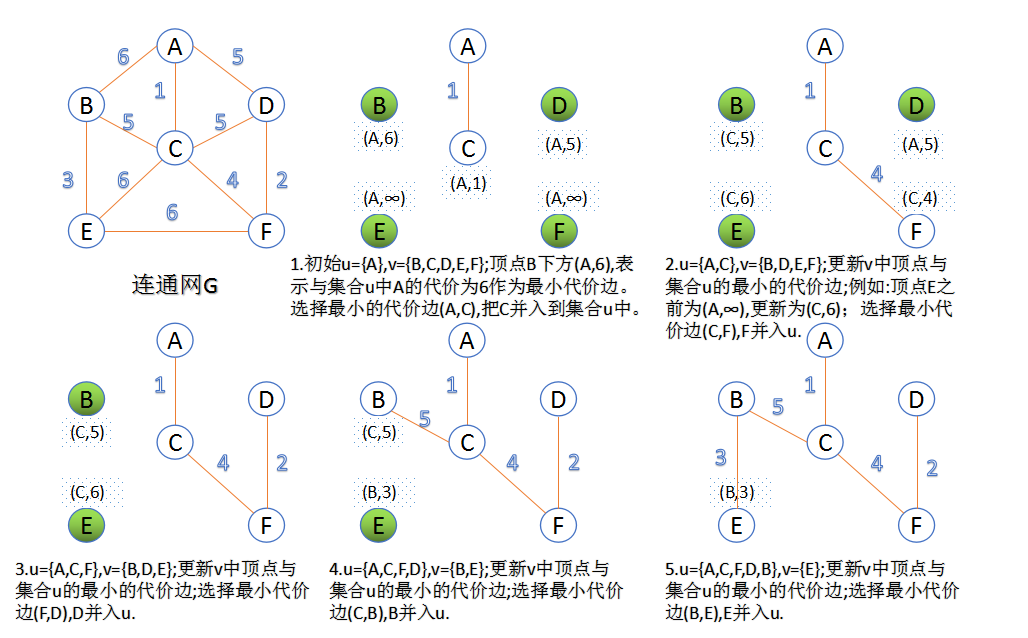
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={ s }, v = V - u;u={s}
- 在两个集合u,v 能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息,:
struct
{
char vertexData //表示u中顶点信息
UINT lowestcost //最小代价
}closedge[vexCounts]- 1
- 2
- 3
- 4
- 5
原作者代码实现采用的C++,这里还是老样子,稍后贴上Java实现代码...
Kruskal 实现
import java.util.ArrayList;
import java.util.List;
/**
* 最小生成树之Kruskal算法
* 1. 把图中的所有边按代价从小到大排序;
2. 2.把图中的n个顶点看成独立的n棵树组成的森林;
3. 3.按权值从小到大选择边,所选的边连接的两个顶点ui,vi,应属于两颗不同的树,则成为最小生成树的一条边, 并将这两颗树合并作为一颗树。
4. 4.重复3,直到所有顶点都在一颗树内或者有n-1条边为止。
* @author Beat IT 2018-1-30
*
*/
public class Kruskal {
// 当两个顶点没有连线的时候将其权值设为MOUSTMAX
private static final int MOUSTMAX = 1000;
// 保存点集的第一个集合
private static List<String> START = new ArrayList<String>();
// 保存点集的第二个集合
private static List<String> END = new ArrayList<String>();
public static void main(String[] args) {
//边数
int count = 10;
//使用邻接矩阵存储图信息 其中顶点从0-5
int[][] adjMat = new int[6][6];
//赋初值
for (int i = 0; i < adjMat.length; i++) {
for (int j = 0; j < adjMat.length; j++) {
adjMat[i][j] = MOUSTMAX;
}
}
//输入边的权值
adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
adjMat[1][2] = 5; adjMat[1][4] = 3;
adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
adjMat[3][5] = 2;
adjMat[4][5] = 6;
//调用排序
while (count>0) {
Kruskal.sort(adjMat);
count--;
}
}
public static void sort(int[][] array){
int min = array[0][0];
//找到当前数组中最小的值
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length; j++) {
if(array[i][j]<=min){
min = array[i][j];
}
}
}
//定义两个变量存储相应坐标,二维数组中有array[0][0]所以如下定义
int varx = Integer.MAX_VALUE;
int vary = Integer.MAX_VALUE;
//将最小处的值改变
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length; j++) {
if(array[i][j] == min){
array[i][j] = MOUSTMAX;
varx = i;
vary = j;
break;
}
}
}
//将数字转化为字符
String charx = Kruskal.tochar(varx);
String chary = Kruskal.tochar(vary);
//判断是否有环路
List<String> laststring = Kruskal.dest(charx,chary);
for (String i : laststring) {
System.out.println(i+" ");
}
}
public static List<String> dest(String charx, String chary){
List<String> last = new ArrayList<String>();
//初始点集为空时
if(END.size()==0){
last.add(charx + chary);
END.add(charx);
END.add(chary);
}else{
// 边的坐标并不全在两个点集中的任何一个点集中
if (!(END.contains(charx) && END.contains(chary) || START.contains(charx)&& START.contains(chary))) {
// 如果 某点在一个点集中,另一个点在另一个点集中
if (END.contains(charx) && START.contains(chary)) {
last.add(charx + chary);
// 构成新的点集
for (String char1 : START) {
if (!END.contains(char1)) {
END.add(char1);
}
}
START.clear();
}
if (START.contains(charx) && END.contains(chary)) {
last.add(charx + chary);
for (String char1 : START) {
if (!END.contains(char1)) {
END.add(char1);
}
}
}
// 如果两点都不在某点集中,那么添加另外一个集合保存新的点集
if (!END.contains(charx) && !END.contains(chary)) {
last.add(charx + chary);
if (!START.contains(charx) && !START.contains(chary)) {
START.add(charx);
START.add(chary);
}
if (START.contains(charx) && !START.contains(chary)) {
START.add(chary);
}
if (!START.contains(charx) && START.contains(chary)) {
START.add(charx);
}
}
}
}
return last;
}
public static String tochar(int var) {
String char1 = "";
switch (var) {
case 0:
char1 = "A";
break;
case 1:
char1 = "B";
break;
case 2:
char1 = "C";
break;
case 3:
char1 = "D";
break;
case 4:
char1 = "E";
break;
case 5:
char1 = "F";
break;
}
return char1;
}
}Prim算法实现
/**
* 最小生成树之Prim算法
* @author Beat IT 2018-2-3
*
*/
public class Prim {
public static void prim(int num, float[][] weight) { //num为顶点数,weight为权
float[] lowcost = new float[num + 1]; //到新集合的最小权
int[] closest = new int[num + 1]; //代表与s集合相连的最小权边的点
boolean[] s = new boolean[num + 1]; //s[i] == true代表i点在s集合中
s[1] = true; //将第一个点放入s集合
for(int i = 2; i <= num; i++) { //初始化辅助数组
lowcost[i] = weight[1][i];
closest[i] = 1;
s[i] = false;
}
for(int i = 1; i < num; i++) {
float min = Float.MAX_VALUE;
int j = 1;
for(int k = 2; k <= num; k++) {
if((lowcost[k] < min) && (!s[k])) {//根据最小权加入新点
min = lowcost[k];
j = k;
}
}
System.out.println("加入点" + j + ". " + j + "---" + closest[j]);//新加入点的j和与j相连的点
s[j] = true;//加入新点j
for(int k = 2; k <= num; k++) {
if((weight[j][k] < lowcost[k]) && !s[k]) {//根据新加入的点j,求得最小权
lowcost[k] = weight[j][k];
closest[k] = j;
}
}
}
}
public static void main(String[] args) {
float m = Float.MAX_VALUE;
float[][] weight = {{0, 0, 0, 0, 0, 0, 0},
{0, m, 6, 1, 5, m, m},
{0, 6, m, 5, m, 3, m},
{0, 1, 5, m, 5, 6, 4},
{0, 5, m, 5, m, m, 2},
{0, m, 3, 6, m, m, 6},
{0, m, m, 4, 2, 6, m}};//上图的矩阵
prim(weight.length - 1, weight);
}
}






















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








