B - 矩形面积
Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u
Description
小度熊有一个桌面,小度熊剪了很多矩形放在桌面上,小度熊想知道能把这些矩形包围起来的面积最小的矩形的面积是多少。
Input
第一行一个正整数 T,代表测试数据组数(


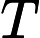

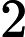
 ),接下来 T 组测试数据。
),接下来 T 组测试数据。
每组测试数据占若干行,第一行一个正整数










 ,代表矩形的数量。接下来 N 行,每行 8 个整数
,代表矩形的数量。接下来 N 行,每行 8 个整数






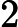


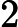











 ,代表矩形的四个点坐标,坐标绝对值不会超过10000。
,代表矩形的四个点坐标,坐标绝对值不会超过10000。


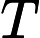

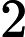
 ),接下来 T 组测试数据。
),接下来 T 组测试数据。 每组测试数据占若干行,第一行一个正整数











 ,代表矩形的数量。接下来 N 行,每行 8 个整数
,代表矩形的数量。接下来 N 行,每行 8 个整数






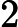


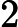











 ,代表矩形的四个点坐标,坐标绝对值不会超过10000。
,代表矩形的四个点坐标,坐标绝对值不会超过10000。 Output
对于每组测试数据,输出两行:
第一行输出"Case #i:",i 代表第 i 组测试数据。
第二行包含1 个数字,代表面积最小的矩形的面积,结果保留到整数位。
第一行输出"Case #i:",i 代表第 i 组测试数据。
第二行包含1 个数字,代表面积最小的矩形的面积,结果保留到整数位。
Sample Input
2 2 5 10 5 8 3 10 3 8 8 8 8 6 7 8 7 6 1 0 0 2 2 2 0 0 2
Sample Output
Case #1: 17 Case #2: 4
题意:给出n个矩形,求能覆盖所有矩形的最小的矩形的面积。
题解:对所有点求凸包,然后旋转卡壳,对没一条边求该边的最左最右和最上的三个点。
利用叉积面积求高,利用点积的性质求最左右点和长度,更新面积最小值即可。
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #define MAX 50010 using namespace std; struct Point{ double x,y; Point(double x=0,double y=0):x(x),y(y){} }; Point P[MAX],ch[MAX]; typedef Point Vector; typedef Point point; Vector operator - (Point A,Point B) { return Vector(A.x-B.x,A.y-B.y); } bool operator <(const Point &a,const Point &b) { return a.x<b.x||(a.x==b.x&&a.y<b.y); } const double eps=1e-10; int dcmp(double x) { if(fabs(x)<eps) return 0; else return x<0?-1:1; } bool operator ==(const Point &a,const Point &b) { return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0; } double Cross(Vector A,Vector B) { return A.x*B.y-A.y*B.x; } double dot(Vector A,Vector B) { return A.x*B.x+A.y*B.y; } int ConvexHull(Point *p,int n) { sort(p,p+n); n=unique(p,p+n)-p; int m=0; for(int i=0;i<n;i++) { while(m>1&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<0) m--; ch[m++]=p[i]; } int k=m; for(int i=n-2;i>=0;i--) { while(m>k&&Cross(ch[m-1]-ch[m-2],p[i]-ch[m-2])<=0) m--; ch[m++]=p[i]; } if(n>1) m--; return m; } double Length(Vector A) { return dot(A,A); } double rotating_calipers(Point *p,int n) { int l=1,r=1,w; double ans=1e30; p[n]=p[0]; for(int i=0;i<n;i++) { //注意这里等于0一定要算上 //这里debug了整整一个小时 - -||||| //找到至高点 while(dcmp(Cross(p[i+1]-p[i],p[w+1]-p[i])-Cross(p[i+1]-p[i],p[w]-p[i]))>=0) //因为边平行的时候面积相等 虽然如此但还是要继续找下一个 横着爬不动的意思 w=(w+1)%n; //找到最右的点 不可能向左的 while(dcmp(dot(p[i+1]-p[i],p[r+1]-p[i])-dot(p[i+1]-p[i],p[r]-p[i]))>0) //凸包不可能凹进去 所以不需要等号 加深对凸包求解过程的理解 r=(r+1)%n; if(i==0) l=r; while(dcmp(dot(p[i+1]-p[i],p[l+1]-p[i])-dot(p[i+1]-p[i],p[l]-p[i]))<=0) //必须加等号 否则凸包遇到直边的时候拐不过来 上不去 第二组样例可以完美说明问题 l=(l+1)%n; double d=Length(p[i+1]-p[i]); double area=fabs(Cross(p[i+1]-p[i],p[w]-p[i])) *fabs(dot(p[i+1]-p[i],p[r]-p[i])-dot(p[i+1]-p[i],p[l]-p[i]))/d; //cout<<fabs(Cross(p[i+1]-p[i],p[w]-p[i]))<<" "; //cout<<"rrrrr "<<r<<" lll "<<l<<endl; //cout<<dot(p[i+1]-p[i],p[r]-p[i])<<" "<<dot(p[i+1]-p[i],p[l]-p[i])<<endl; ans=min(ans,area); } return ans; } int main() { int t,n,cas=1; scanf("%d",&t); while(t--) { scanf("%d",&n); n*=4; for(int i=0;i<n;i++) scanf("%lf%lf",&P[i].x,&P[i].y); int m=ConvexHull(P,n); //for(int i=0;i<n;i++) //cout<<ch[i].x<<" "<<ch[i].y<<endl; double ans; if(m<3) ans=0; else ans=rotating_calipers(ch,m); long long tmp = ans+0.5; printf("Case #%d:\n%lld\n",cas++,tmp); } return 0; }
分析过程:























 258
258

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








