遗传算法(Genetic Algorithm,GA)由霍兰德教授在20世纪70年代提出,是以自然选择和遗传变异为理论依据的全局性概率搜索优化算法模型。采用遗传算法寻优时需要将问题的候选解进行编码,即一个候选解对应一个编码,编码通常采用二进制,用“0”、“1”表示,为“1”则表示该候选解被选中,所有候选解组合在一起定义为染色体;在迭代进化的过程中,通过构造适应度函数,计算每个个体的适应度,适应度值越大,该个体被保留的可能性越大。
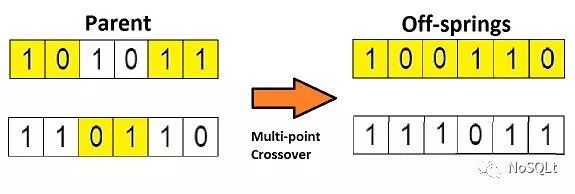
遗传算法主要操作包括选择、交叉、变异。选择是指依据适应度值优胜劣汰的过程;交叉是指两个父代个体的结构按照一定的概率Pc(交叉概率,也称交叉率)相互交换产生新个体的过程;变异是以一个很小的概率Pm(变异概率,也称变异率)随机将个体的基因值从“0”变成“1”或“1”变成“0”的过程. Pc和Pm的大小对于算法的优化效率影响很大,Pc越大表示当前父代的染色体结构复制到下一代的比例较少,与另一个父代染色体结构交换的比例越大,而这样,父代的染色体的结构破坏较大;当Pm较大时,则代表父代染色体的结构在下一次迭代优化时会发生较大概率的突变。因此,为了提高算法的优化效率,在迭代优化的早期,较大的Pc和Pm,在迭代优化后期较小的Pc和Pm有利于算法效率的提高。普通的遗传算法将上述两个概率值设置为固定值,限制了算法的优化效率,而自适应遗传算法(Adaptive Genetic Algorithm)将上述Pc和Pm的值依据适应度值在迭代优化时动态调整,提高了算法的优化效率(下面只列举一种Pc和Pm的自适应算法)。
1:交叉(多点交叉),其他种类的交叉算法详见https://blog.csdn.net/u012750702/article/details/54563515/
2:变异

3:自适应遗传算法的举例(其他的自适应算法读者可搜索文献)
![]()
![]()
式中,fmax代表种群中最佳适应度值;favg代表每代种群的平均适应度值;'![]() 代表要交叉的两个个体中较大的适应度值;f代表要变异的个体的适应度值;k1=k2=0.6;k3=k4=0.1。
代表要交叉的两个个体中较大的适应度值;f代表要变异的个体的适应度值;k1=k2=0.6;k3=k4=0.1。
4:适应度函数的设置
适应度函数的设置对于遗传算法的优化系哦啊绿至关重要,而在不同的优化问题中,适应度函数的设置需要根据具体的优化问题而言,就常见的机器学习分类问题而言,fitness=w1×f1+w2×accuracy;其中 w1和w2分别代表权重系数,两者之和为1,f1代表用到的建模变量个数,accuracy代表分类的精度(比如OA,kappa等)。对于机器学习的回归问题,fitness=.R2表示决定系数,RMSE表示均方根误差(文章 DOI: 10.1080/01431161.2020.1718239.)。对于适应度值得设置,应当尽量放大体间的差异。
5:迭代结束的设置
可以依据适应度值在保持多少代不变或者设定一个阈值,当适应度值相邻两代的差值低于该阈值时,就停止进化迭代,或者设置最大的遗传迭代次数。
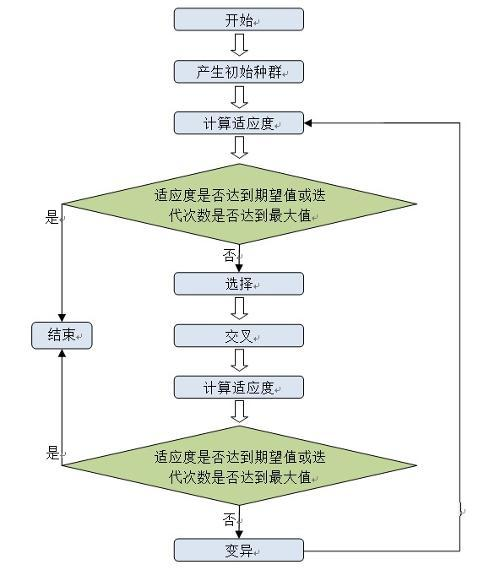
6: 遗传算法的具体使用流程
(1).编码、随机产生初始群体;
(2)个体评价、选择、确定是否输出;
(3)随机交叉运算;
(4)随机变异运算;
(5)转向个体评价,开始新循环
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










