刷题第七天（最大正方形与矩形）问题（单调栈与动态整理，待补充）

221. 最大正方形

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4
示例 2：

输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1
示例 3：

输入：matrix = [[“0”]]
输出：0

//每一个下标是由左，上，左上决定的
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
     int n=matrix.size();
     int m=matrix[0].size();
     int res=0;
     for(int i=0;i<n;i++){
         for(int j=0;j<m;j++){
             if(i==0||j==0||matrix[i][j]=='0'){
                res=max(matrix[i][j]-'0',res);
             }
             else{
               matrix[i][j]=char(min(min(matrix[i-1][j]-'0',matrix[i][j-1]-'0'),matrix[i-1][j-1]-'0')+1+'0');
               res=max(res,matrix[i][j]-'0');
             }
         }
     }
     return res*res;
    }
};

85. 最大矩形

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

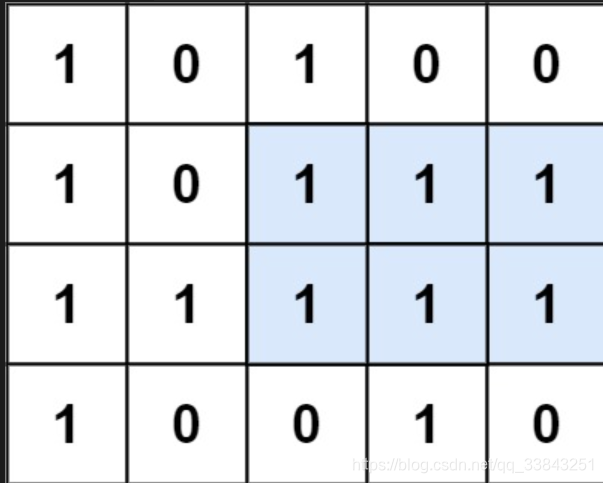
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：6
解释：最大矩形如上图所示。
示例 2：

输入：matrix = []
输出：0
示例 3：

输入：matrix = [[“0”]]
输出：0
示例 4：

输入：matrix = [[“1”]]
输出：1
示例 5：

输入：matrix = [[“0”,“0”]]
输出：0

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.size()==0||matrix[0].size()==0){
            return 0;
        }
     vector<vector<int>> vec(matrix.size(),vector<int>(matrix[0].size(),0));
     for(int i=0;i<matrix.size();i++){
         for(int j=0;j<matrix[0].size();j++){
             if(j==0||matrix[i][j]=='0'){
                 vec[i][j]=matrix[i][j]-'0';
             }
              else {
                  vec[i][j]=vec[i][j-1]+1;
             }
         }
     }
     int res=0;
     for(int i=0;i<vec.size();i++){
         for(int j=0;j<vec[0].size();j++){
             if(vec[i][j]!=0){
              int width=vec[i][j];//长度初始化
              int area=width;//面积初始化
              for(int k=i-1;k>=0;k--){
               width=min(width,vec[k][j]);
                area=max(area,width*(i-k+1));
              }
              res=max(res,area);
             }
         }
     }
     return res;
    }
};

//单调栈

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        if(matrix.size()==0||matrix[0].size()==0){
            return 0;
        }
        int ans=0;
    vector<int> dp(matrix[0].size()+2,0);
     for(int i=0;i<matrix.size();i++){
         for(int j=0;j<matrix[0].size();j++){
             if(matrix[i][j]=='0'){
                 dp[j+1]=0;
             }
              else {
                 dp[j+1]=dp[j+1]+1;
             }
         }
        ans=max(ans,bigErae(dp));   
     }
    return ans;
    }
    int bigErae(vector<int>&dp){
        stack<int> st;
        int res=0;
        for(int i=0;i<dp.size();i++){
            while(!st.empty()&&dp[st.top()]>dp[i]){
                int temp=st.top();
                st.pop();
                int cur=st.top();
                res=max(res,dp[temp]*(i-cur-1));
               
            }
            st.push(i);
        }
      return res;
    }
};

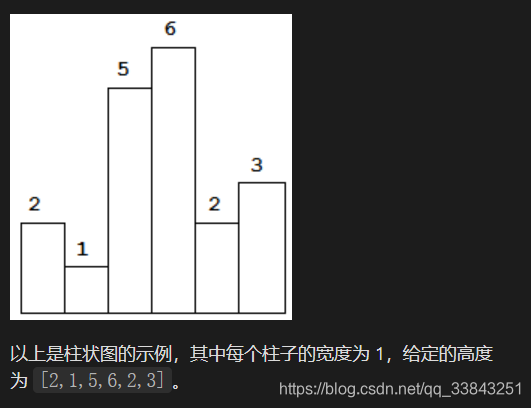
84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
       if(heights.size()==0) return 0;
       heights.insert(heights.begin(),0);
       heights.push_back(0);
       stack<int> st;
       int ans=0;
       for(int i=0;i<heights.size();i++){
           while(!st.empty()&&heights[st.top()]>heights[i]){
               int temp=st.top();
               st.pop();
               ans=max(ans,(i-st.top()-1)*heights[temp]);

           }
           st.push(i);
       } 
       return ans;
    }
};

1504. 统计全 1 子矩形

给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

输入：mat = [[1,0,1],
[1,1,0],
[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
示例 2：

输入：mat = [[0,1,1,0],
[0,1,1,1],
[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。
示例 3：

输入：mat = [[1,1,1,1,1,1]]
输出：21
示例 4：

输入：mat = [[1,0,1],[0,1,0],[1,0,1]]
输出：5

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
     int n=mat.size();
     int m=mat[0].size();
     //统计长度
     for(int i=0;i<n;i++){
         for(int j=0;j<m;j++){
             if(j==0||mat[i][j]==0){
                 mat[i][j]=mat[i][j];
             }
             else{
                 mat[i][j]=mat[i][j-1]+1;
             }
         }
     }
     int ans=0;
     for(int i=0;i<n;i++){
         for(int j=0;j<m;j++){
             if(mat[i][j]!=0){
                 int temp=mat[i][j];
                 for(int k=i;k>=0;k--){
                     if(mat[k][j]==0){
                         break;
                     }
                     temp=min(mat[k][j],temp);
                      ans+=temp;
                 }
             }
         }
     }
     return ans;
    }
};

1277. 统计全为 1 的正方形子矩阵

给你一个 m * n 的矩阵，矩阵中的元素不是 0 就是 1，请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。

示例 1：

输入：matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出：15
解释：
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.
示例 2：

输入：matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
输出：7
解释：
边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.

class Solution {
public:
    int countSquares(vector<vector<int>>& matrix) {
      int n=matrix.size();
      int m=matrix[0].size();
      int res=0;
      for(int i=0;i<n;i++){
          for(int j=0;j<m;j++){
            if(matrix[i][j]==0){
                continue;
            }
            else if(i==0||j==0){
                res++;
            }
            else{
                matrix[i][j]=min(min(matrix[i][j-1],matrix[i-1][j]),matrix[i-1][j-1])+1;
                res+=matrix[i][j];
            }
          }
      }
     return res; 
    }
};

1727. 重新排列后的最大子矩阵

给你一个二进制矩阵 matrix ，它的大小为 m x n ，你可以将 matrix 中的 列 按任意顺序重新排列。

请你返回最优方案下将 matrix 重新排列后，全是 1 的子矩阵面积。

class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& m) {
        int res=0;
     vector<int> dp(m[0].size()+1,0);
        for(int i=0;i<m.size();i++){
            for(int j=0;j<m[0].size();j++){
                if(m[i][j]==1){
                      dp[j]=dp[j]+1;
                }
                else{
                    dp[j]=0;
                }

            }
            res=max(res,big(dp));
        }
        return res;
    }
    int big(vector<int> dp){
        sort(dp.begin(),dp.end());
        dp.push_back(0);
        stack<int> st;
        int ans=0;
       for (int i = 0; i < dp.size(); i++) {
			while (!st.empty() && dp[st.top()] > dp[i]) {
				int cur = st.top();
				st.pop();
				ans = max(ans, (i-cur) * dp[cur]);
			}
			st.push(i);
		}


        return ans;
    }
};

#267. 废土游戏

题目描述
​ 有一天，小明和李华来到了世外桃源，桃园主要赏赐给他们一块土地。

​ 这片土地被分成 N∗M个格子，每个格子里写着 R 或者 F，R 代表这块土地被赐予了小明，F 代表这块土地被赐予了李华。现在李华要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着 F 并且面积最大。现在他们求助于你，如果你找到的土地面积为S，它们每人给你 3∗S 两银子。

输入
​ 第一行两个整数 N,M，表示矩形土地有 N 行 M 列。

​ 接下来 N 行，每行 M 个用空格隔开的字符 F 或 R，描述了矩形土地。

输出
​ 输出一个整数，表示你能得到多少银子，即 3∗MAX(S) 的值。

样例输入
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
样例输出
45

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
int big(vector<int> dp) {
	vector<int> vec;
	int ans = 0;
	for (int i = 0; i < dp.size(); i++) {
		while (!vec.empty() && dp[vec.back()] > dp[i]) {
			int temp = vec.back();
			vec.pop_back();
			ans = max(ans, (i - vec.back() - 1) * dp[temp]);
		}
		vec.push_back(i);
	}
	return ans;
}
int main() {
	int n,m;
	cin >> n >> m;
	vector<vector<char>> vec(n, vector<char>(m));
	vector<int> dp(m + 2, 0);
	int ans = 0;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			cin >> vec[i][j];
		}
	}
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			if (vec[i][j] == 'F') {
				dp[j + 1] = dp[j + 1] + 1;
			}
			else {
				dp[j + 1] = 0;
			}
		}
		ans = max(ans, big(dp));
	}
	cout << 3 * ans << endl;

}