[近似算法] 多机调度和装箱问题

性能度量

Def 5 性能比
设$A$是优化问题$\Pi$的一个近似算法，算法$A$在一个输入实例$I$上的性能比$R_A(I)$被定义为：
$$R_A(I)=\{\begin{array}{l}\frac{A(I)}{OPT(I)}\text{ if }\Pi \text{ 是最小化问题 }\\ \frac{OPT(I)}{A(I)}\text{ if }\Pi \text{ 是最大化问题 }\end{array}$$
此定义统一使近似比(性能比) $R_A(I)\ge 1$，越接近1越好, 若$R_A(I)\le （1+∊）$，则称$A$是$(1+∊)$－近似算法 (1-近似算法即产生最优解

Def 6 绝对性能比
对于优化问题$\Pi$，近似算法$A$的绝对性能比$R_A$是 R A = i n f { r │ R A ( I ) ≤ r , ∀ I ∈ D } R_A= inf\{ r│R_A(I) ≤r, ∀I∈D \} RA​=inf{r│RA​(I)≤r,∀I∈D}
即：$R_A$是性能比上界集合中的下确界(最大下界)

Def 7 渐进性能比
一个优化问题$\Pi$的近似算法$A$, 其渐近性能比为:
$$R_A^{\infty }=\inf \left\{r\mid \exists N\in Z^{+},R_A(I)\le r\text{ for }\forall I\in D_{\Pi }\text{ with }OPT(I)\ge N\right\}$$
直观解释就是输入实例趋近于无穷大时的性能比收敛到一个确切上界, 这个上界称为渐进性能比.

联系
对于有Scaling性质的问题, 近似算法的绝对性能比和渐近性能比是相同的.
scaling性质指线性变化的输入实例, 会得到相应线性变化的问题的解, 比如0/1背包问题中, 如果利润成比例$N$增加到$N{p}_i,i=1,2,...,n$ 其他参数不变, 则最优解$OPT(I)$和近似解$A(I)$也会相应成$N$倍增加到$N\ast OPT(I)$和$N\ast A(I)$ (因为装包组合方式不会因为利润都成倍变化而改变, 所以相同的装包组合一定会产生对应倍率的总利润

再看性能比的定义
$$R_A(I)=\{\begin{array}{l}\frac{A(I)}{OPT(I)}\text{ if }\Pi \text{ 是最小化问题 }\\ \frac{OPT(I)}{A(I)}\text{ if }\Pi \text{ 是最大化问题 }\end{array}$$
既然问题具有scaling性质, 容易得到绝对性能比与输入实例规模无关的结论(分子分母同倍增加或减小不会改变比值), 则只要输入规模足够大使得$OPT(I)\ge N$, 即可满足渐进性能比定义, 此时性能比就同时是绝对性能比和渐进性能比, 即两个性能比相等.

多机调度问题

考虑简单的多机调度问题：输入n个作业$J_1，J_2，\dots ，J_n$，相应的运行时间为$P_1，P_2，\dots ，P_n$，设每个$P_i$是有理数。将n个作业分配到m台同样的机器上，以使得完成时间最短。
完成时间定义为：所有机器上作业运行总时间最长的那一台机器的运行时间。
可行解集合：n个作业被划分为m个子集，一个解的值是所有子集中总运行时间最长的子集的运行时间。该问题即使在m=2时也是NP-hard的

List调度算法(Graham)：将n个作业依次以online的方式分配到m台机器中的某一台上，规则是将当前作业分配到当时负载最小的机器上，而机器负载是当前分配给它的所有作业的总的运行时间.

总体来说证明需要证: (1) 求出上界 (2) 证明紧确
由三个观察出来的不等式联立推出上界表达式

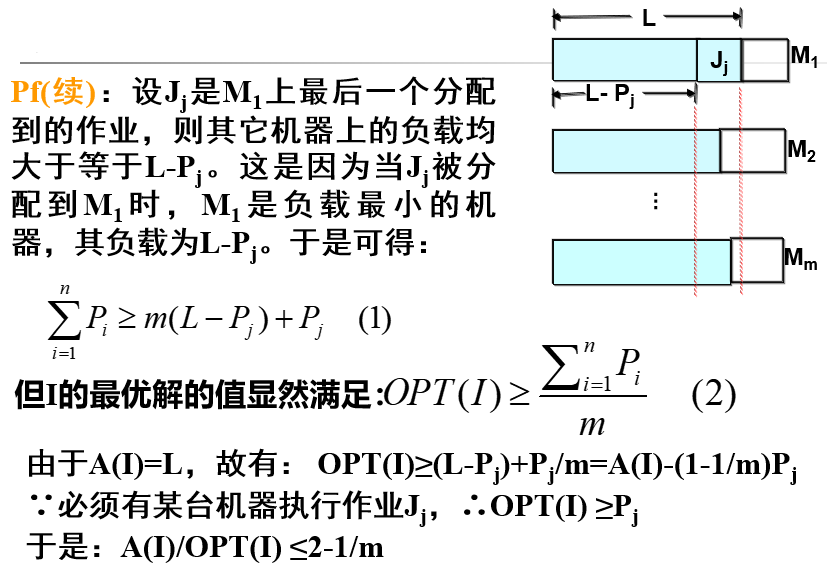
证明紧确只需要找到一个例子能够使等号成立

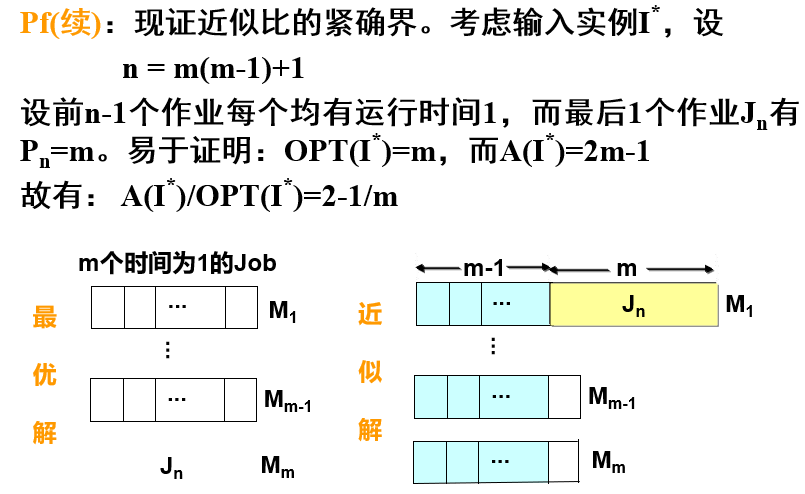
更好的调度是LPT(Longest Processing Time)：将作业按其运行时间递减序排序, 然后用List策略调度

装箱问题

装箱定义：设有n件物品，每件物品大小$S_i\in [0,1](1\le i\le n)$，按某种策略将其装入大小为1的若干箱子中，使箱子数尽可能小.

先排序再装包可以优化渐进性能比, 这里渐进性能比和绝对性能比不一致, (ppt中 $R_{FFD}\ge 3/2$ 不准确), 性能比可以为1, 比如(1), 此时次优解就是最优解, 3/2的情况是输入实例为（1/2, 1/3）,（ 1/3, 1/3, ¼）,（ ¼）FFD算法需要3个包, 实际最优解为(1/2, 1/4, 1/4), (1/3, 1/3, 1/3) 2个包即可.