树状数组学习（例题及题解）

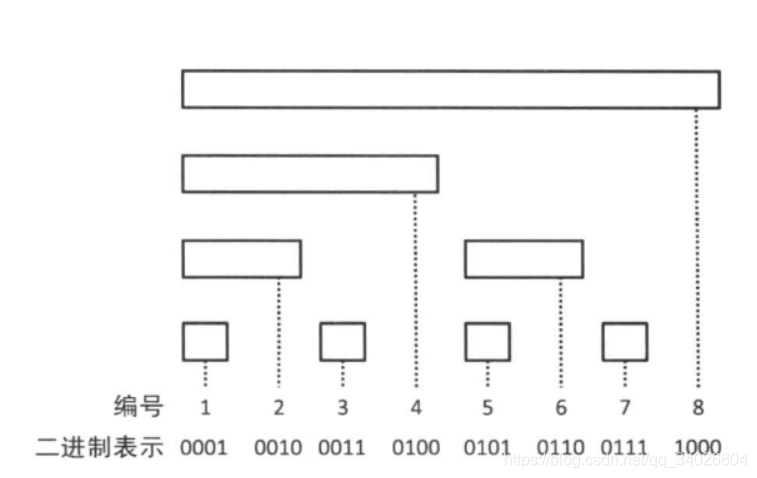
树状数组：可以动态维护前缀和，查询时间复杂度O（log₂n）,修改时间复杂度O（log₂n）。
树状数组记录前缀和的方式为这个数的二进制表示中从长度是从右往左的第一个0的大小,即长度为x-lowbit(x)+1。
代码模板

int tr[N];
int lowbit(int x)   //求第一个0的位置
{
    return x & -x;
}

void add(int x, int c) 在位置为x的地方加上c
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int sum(int x) 求x的前缀和
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

树状数组题解
1.楼兰图腾

大致思路：对于点i，求出左边和右边比i小的个数相乘，即为在i点∧的个数，同理，求出左边和右边比i大的个数相乘，即为在i点V的个数。
故可以用两个数组记录
Low[i]表示左边比第i个位置小的数的个数
Great[i]表示左边比第i个位置大的数的个数
tr[i]求和表示用于记录小于等于i个数的总和

const int N=200010;

int n;
int a[N],tr[N];
int great[N],low[N];

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i))
        tr[i]+=c;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    
    return res;
}
int main()
{
    cin>>n;
    
    for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
    
    for(int i=1;i<=n;i++)    从左往右遍历
    {
        int y=a[i];
        
        low[i]=sum(y-1);  
        great[i]=sum(n)-sum(y);
        
        add(y,1);
    }
    
    int res1=0,res2=0;
    memset(tr,0,sizeof tr); 
    
    for(int i=n;i;i--)  从右往左遍历出右边比i大和小的数
    {
        int y=a[i];
        
         res1+=(sum(n)-sum(y))*great[i];
         res2+=sum(y-1)*low[i];
        
        add(y,1);
    }
    
    printf("%d\n%d",res1,res2);
    
    return 0;
}

2.一个简单的整数问题
大致思路：本题是将树状数组和差分相结合，动态维护差分数组。
bi为差分数组，则Ai=b1+b2+b3+…+bi。
即l,r加上d就变为数组l位置加上d，r+1位置减去d。
差分数组bi=A[i]-A[i-1]
读入时

 for (int i = 1; i <= n; i ++ ) add(i, a[i] - a[i - 1]);

查询时

printf("%lld\n", sum(x))

修改时

add(l, d), add(r + 1, -d);

3.一个简单的整数问题2

题目相较于上一个变为查询l~r之和。
差分数组计算变为

将整个数组的矩阵列出

然后将空余的地方补齐

那么可发现

对于数组A的（1到x）的前缀和可表示为差分数组b(1到x)的前缀和×（x+1）-（i*bi）的前缀和
那么构建数组tr1维护bi的前缀和
构建数组tr2维护i*bi的前缀和

维护树状数组操作

ll a[N];
ll tr1[N],tr2[N];

int lowbit(int x)
{
    return x&-x;
}

void add(ll tr[],int x,ll k)
{
    for(int i=x;i<=n;i+=lowbit(i)) 
        tr[i]+=k;
}

ll sum(ll tr[],int x)
{
    ll res=0;
    for(int i=x;i;i-=lowbit(i))
        res+=tr[i];
    return res;
}

ll pre_sum(int x)  //计算A数组1~x的前缀和
{
    return sum(tr1,x)*(x+1)-sum(tr2,x);
}

读入时操作

for(int i=1;i<=n;i++)
    {
        int b=a[i]-a[i-1];
        add(tr1,i,b);
        add(tr2,i,(ll)i*b);
    }

查询时操作

cout<<pre_sum(r)-pre_sum(l-1)<<endl;

修改时操作

add(tr1,l,d);
            add(tr1,r+1,-d);
            add(tr2,l,l*d);
            add(tr2,r+1,(r+1)*-d);