Provable Security for Public-Key Schemes
Cryptography
secrecy of communications
practical secrecy
Shannon provides a definition of secrecy
Perfect Secrecy:
The ciphertext does not reveal any(additional) information about the plaintext:no more than known before
- a prior information about the plaintext,defined by the distribution probability of the plaintext,
- a posterior information about the plaintext,defined by the distribution probability of the plaintext,given the ciphertext
Both distributions should be perfectly identical
Perfect Secrecy vs. Practical Secrecy
No information about the plaintext m is in the ciphertext c without the knowledge of the key k
⇒ information theory
No information about the plaintext m can be extracted
from the ciphertext c, even for a powerful adversary (unlimited time and/or unlimited power): perfect secrecy
In practice: adversaries are limited in time/power
⇒ complexity theory
Asymmetric Encryption: Intuition
Secrecy:
- The recipient only should be able to open the message
- No requirement about the sender
Asymmetric Encryption: Formalism
Public Key Cryptography – Diffie-Hellman (1976)
- Bob’s public key is used by Alice as a parameter to encrypt a message to Bob
- Bob’s private key is used by Bob as a parameter to decrypt ciphertexts
Secrecy of the private key sk ⇒ secrecy of communications
Because of pk,perfect secrecy is definitely impossible!
Provable Security
What is a Secure Cryptographic Scheme/Protocol?
- Public-key encryption:Secrecy of the private key sk ⇒ secrecy of communications
- What does mean secrecy? → Security notions have to be formally defined
- How to guarantee above security claims for concrete schemes?→ Provable security
One can prove that:
if an adversary is able to break the cryptographic scheme
then one can break a well-known hard problem
General Method
Computational Security Proofs
In order to prove the security of a cryptographic scheme/protocol,one needs
- a formal security model (security notions)
- acceptable computational assumptions (hard problems)
- a reduction: if one can break the security notions,
then one can break the hard problem
Computational Assumptions
Integer Factoring
- Given n = pq
- Find p and q
Integer Factoring Variants(变体/变种/变形)
未解难题:RSA问题是否等价于IFP?目前仅已知(难度上)RSAP<=IFP。换句话说,RSA假设要强于IF假设。
RSA
- Given n = pq, e and y ∈ Zn*
- Find x such that y = xe mod n
Note that this problem is hard without the prime factors p and q, but becomes easy with them: if d = e−1 mod ϕ(n), then x = yd mod n
** Flexible RSA **
- Given n = pq and y ∈ Zn*
- Find x and e > 1 such that y = xe mod n
Both problems are assumed as hard as integer factoring:the prime factors are a trapdoor to find solutions
Discrete Logarithm Problem
- Given G =
a cyclic group of order q, and y ∈ G - Find x such that y = gx
Possible groups: G ∈ (Zp*, ×), or an elliptic curve
(Computational) Diffie Hellman Problem
- Given G =
a cyclic group of order q, and X = g x , Y =g y - Find Z = gxy
The knowledge of x or y helps to solve this problem (trapdoor)
Success Probabilities
For any computational problem P, we quantify the quality of an adversary A by its success probability in finding the so(量化问题的难度):
SuccP(A) = Pr[A(instance) → solution]
We quantify the hardness of the problem by the success probability of the best adversary within time t:
Succ(t) = max|A|≤t{Succ(A)}
Note that the probability space can be restricted:
some inputs are fixed, and others only are randomly chosen
Discrete Logarithm Problem
We usually fix the group G =
of order q, X is randomly chosen:
(Decisional) Diffie Hellman Problem(DDHP)
- Given G =
a cyclic group of order q, and X = g x , Y = g y ,as well as a candidate Z ∈ G - Decide whether Z = gxy
In such a case, the adversary is called a distinguisher (outputs 1 bit) A good distinguisher should behave in significantly different manners according to the input distribution:
 Distribution Indistinguishability
Distribution Indistinguishability
Indistinguishabilities
Let D0 and D1, two distributions on a finite set X:
- D0 and D1 are perfectly indistinguishable if
- D0 and D1 are statistically indistinguishable if
Computational Indistinguishability
Let D0 and D1, two distributions on a finite set X:
a distinguisher A between D0 and D1
 the computational indistinguishability of D0 and D1 is
the computational indistinguishability of D0 and D1 is
Theorem
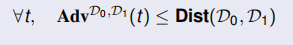









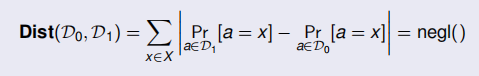














 4147
4147











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








