题意:
给出一个长为M的序列a,其总和为N
先在需要构造出一个序列b,其总和也为N,且满足如下条件:
对于任意一个字符串,如果按照a分为M块,每块内部都为回文,
而且按照b分为M块,没亏内部也为回文。
要求所有满足上述条件的字符串,所有字符都相同。
分析:
其实这道题非常非常水。。。
由于最近刷了很多并查集的题,那么这里利用并查集来解释一下:
对于任意一个回文,我们可以看作连一些边:

所以所有联通的点其种类必须相同。
最终要求只有一种类型,也就意味着所有的线连成了一条。
这样一来,无解条件就很显然了,当a序列中有3个及以上的奇数,则一定无解。
证明非常简单,因为一旦有奇数,在其中间必然有一个单一的点,并且必然是最终的连线的一个端点,一条线只有2个端点,所以如果存在3个及以上单点,则一定无法用一条线连起来。
现在考虑如何构造,首先针对m=1的情况:
一种很好的构造方式是:b1=a1−1,b2=1b1=a1−1,b2=1
画图表示成这个样子:

自己画几个图就会发现,这样无论a1a1是奇是偶都能满足
现在考虑m≠1m≠1的情况:
如果有奇数,就把奇数放在两端,然后按如下规则构造b
b1=a1+1b1=a1+1
bi=ai(1<i<m)bi=ai(1<i<m)
bm=am−1bm=am−1(如果am=1am=1则不要这一位)
自己画几个图也能发现这一定能满足。
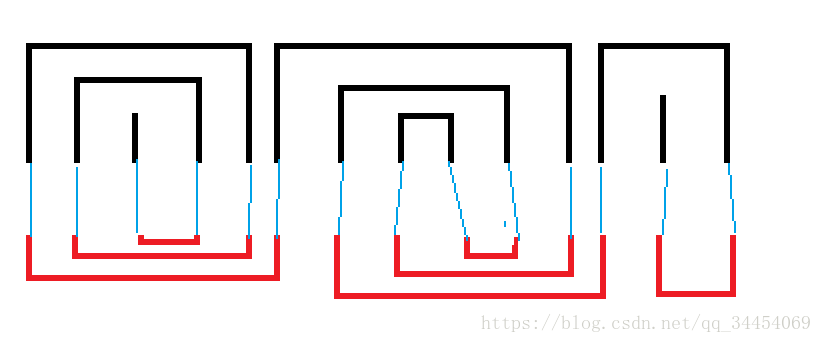
于是,其实根本不需要并查集。。只要学过数组的人都写得出来。。。(近期写的最简单代码,没有之一)
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define SF scanf
#define PF printf
#define MAXN 100010
using namespace std;
int fa[MAXN],a[MAXN],b[MAXN];
int n,m;
int main(){
SF("%d%d",&n,&m);
int cnt=0;
for(int i=1;i<=m;i++){
SF("%d",&a[i]);
if(a[i]%2==1)
cnt++;
}
if(m==1){
PF("%d\n",a[1]);
if(a[1]==1)
PF("1\n1");
else
PF("2\n%d %d",a[1]-1,1);
return 0;
}
if(cnt>2){
PF("Impossible");
return 0;
}
for(int i=1;i<=m;i++)
if(a[i]%2==1){
swap(a[i],a[1]);
break;
}
for(int i=m-1;i>1;i--)
if(a[i]%2==1){
swap(a[i],a[m]);
break;
}
for(int i=1;i<=m;i++)
PF("%d ",a[i]);
b[1]=a[1]+1;
for(int i=2;i<m;i++)
b[i]=a[i];
b[m]=a[m]-1;
if(b[m]==0)
m--;
PF("\n%d\n",m);
for(int i=1;i<=m;i++)
PF("%d ",b[i]);
}




 题目要求构造一个与给定序列a总和相等的序列b,使得两序列按长度分割后每部分都是回文。通过分析,当a序列中有3个及以上奇数时问题无解。对于序列构造,当长度m=1时,有简单解决方案;当m≠1时,将奇数放两端并遵循特定规则构建b。实际上,这个问题并不需要并查集,对数组操作的理解即可解决。
题目要求构造一个与给定序列a总和相等的序列b,使得两序列按长度分割后每部分都是回文。通过分析,当a序列中有3个及以上奇数时问题无解。对于序列构造,当长度m=1时,有简单解决方案;当m≠1时,将奇数放两端并遵循特定规则构建b。实际上,这个问题并不需要并查集,对数组操作的理解即可解决。
















 392
392

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








