数据结构与算法系列20--图

图的概念

在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。树中的元素我们称为节点，图中的元素我们就叫作顶点（vertex）。图中的一个顶点可以与任意其他顶点建立连接关系。我们把这种建立的关系叫作边（edge）。

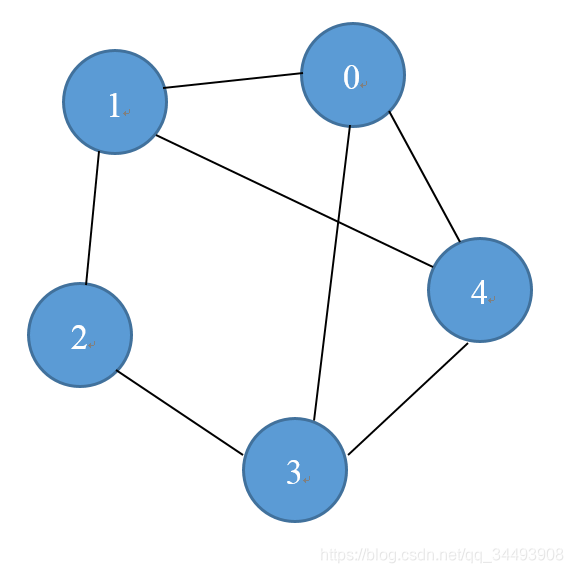
上面的那个图的边是没有方向的，我们称为无向图。
什么是无向图中的度？
跟顶点相连接的边的条数我们就称为度。
另外还有一种有方向的图，我们称为有向图。例如玩过微博的都知道，不同用户之间可以互相关注，如果A用户关注了用户B，我们就把箭头由A指向B，注意它是可以单向关注的，B不一定要有箭头指向A。

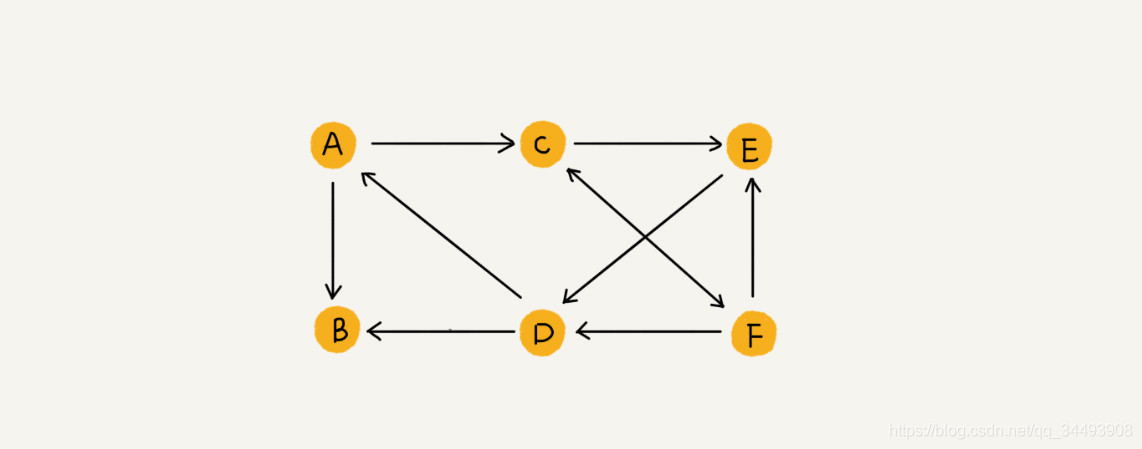
上面的那个图的边是有方向的，我们称为有向图。
有向图的度如何表示？
有向图中我们把度分为入度（In-degree）和出度（Out-degree）。顶点的入度，表示有多少条边指向这个顶点；顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。对应到微博的例子，入度就表示有多少粉丝，出度就表示关注了多少人 。
另外还有一种带权图，在带权图中，每条边都有一个权重（weight）。可以用来表示每一个顶点之间的不同关系。如下：

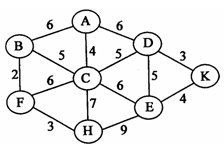
如何在内存中存储图这种数据结构

1.邻接矩阵存储方法

邻接矩阵的底层依赖一个二维数组。对于无向图来说，如果顶点i与顶点j之间有边，我们就将A[i][j] 和 A[j][i] 标记为 1；对于有向图来说，如果顶点i到顶点j之间，有一条箭头从顶点i指向顶点j的边，那我们就将A[i][j] 标记为 1。同理，如果有一条箭头从顶点j指向顶点i的边，我们就将A[j][i]标记为1。对于带权图，数组中就存储相应的权重。
缺点： 用邻接矩阵来表示一个图，虽然简单、直观，但是比较浪费存储空间。
优点： 邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点的关系时，就非常高效。其次，用邻接矩阵存储图的另外一个好处是方便计算。

2.邻接表存储方法

每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。这就是邻接表的储存方法。
缺点： 储存耗时间
优点： 节省空间
前面讲过，链表的储存方式对缓存不友好。所以，比起邻接矩阵的存储方式，在邻接表中查询两个顶点之间的关系就没那么高效了。实际上，我们还可以将邻接表的链表改为更加高效的动态数据结构，比如平衡二叉查找树、跳表、散列表等。