【洛谷 P8692】[蓝桥杯 2019 国 C] 数正方形 题解（组合数学+平面几何）

[蓝桥杯 2019 国 C] 数正方形

题目描述

在一个 $N\times N$ 的点阵上，取其中 $4$ 个点恰好组成一个正方形的 $4$ 个顶点，一共有多少种不同的取法？

由于结果可能非常大，你只需要输出模 $10^9+7$ 的余数。

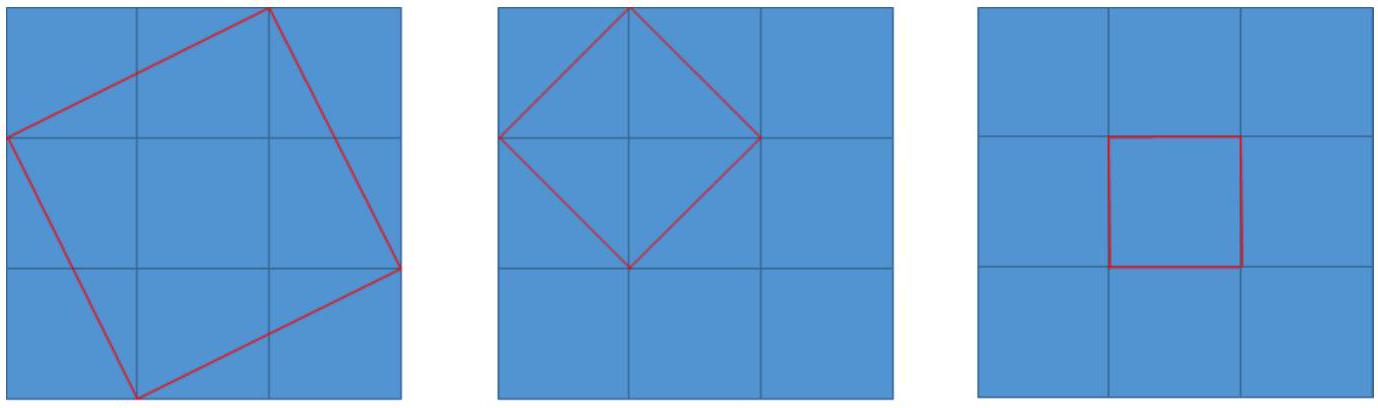
如上图所示的正方形都是合法的。

输入格式

输入包含一个整数 $N$。

输出格式

输出一个整数代表答案。

样例 #1

样例输入 #1

4

样例输出 #1

20

提示

对于所有评测用例，$2\le N\le 10^6$。

蓝桥杯 2019 年国赛 C 组 G 题

---

思路

首先从输入中读取一个整数 $N$，这个整数表示点阵的大小。然后将 $N$ 减一，这是因为在一个 $N\times N$ 的点阵上构成的正方形的最大边长为 $N-1$。然后初始化长整型变量 ans 为 $0$，用来存储最终的结果。

接着进行从 $1$ 到 $n$ 的循环，每一次循环都计算一种边长为 $i$ 的正方形的数量。在循环中，首先计算出在边长为 $n$ 的大正方形中含有多少个边长为 $i$ 的子正方形，这个数量为 $(n-i+1)\times (n-i+1)$。然后将这个数量乘以 $i$，因为边长为 $i$ 的大正方形可以取得 $4$ 个定点在大正方形边上的小正方形。这样就得到了所有边长为 $i$ 的正方形的数量。最后将这个数量累加到 ans 中，并对 $10^9+7$ 取余。

最后输出 ans，这就是在点阵上取 $4$ 个点恰好组成一个正方形的所有可能取法的数量。

---

AC代码

#include <algorithm>
#include <cmath>
#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;

const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9 + 7;

int n;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);

	cin >> n;

    // n * n 点阵构成的正方形边长为 n - 1
	n--;

	ll ans = 0;
	for (int i = 1; i <= n; i++) {
		ll t = (n - i + 1);
		// cout << t * t << endl;
        // 边长为 n 的大正方形中含有 t * t 个边长为 i 的子正方形（正放）
        // 边长为 i 的大正方形可以取得 4 个定点在大正方形边上的小正方形（正放、斜放）
		ans = (ans + (1LL * t * t * i)) % MOD;
	}
	cout << ans << "\n";
	return 0;
}