目录
运动学(Kinematics):从几何观点研究物体位置随时间的变化;
动力学(Dynamics):研究物体的运动与物体间相互作用的联系,阐明物体运动状态发生变化的原因;
静力学:研究物体在相互作用下的平衡问题,可看作动力学的一部分。
一、质点和参考系
1.1、质点
定义:没有体积和形状,只具有一定质量的理想物体,一种理想力学模型,一种物理上的抽象。
物体的体积和形状,如果在研究问题当中作用不大或不影响整体研究结果,就可以当作次要矛盾而忽略掉,物体就被抽象为一个仅有质量的理想化模型即质点。
1.2、参考系
(1)运动绝对性:物体都在运动,没有绝对静止的;
(2)机械运动的相对性:一个物体的位置及其变更,总是相对于其他物体而言的,否则没有意义;
(3)参考系:为了描述物体机械运动,必须选择另一个物体或者物体群作参照物,被选作参照的物体或者物体群称为参考系。
参考系原则上可任意选择。选择使问题的处理尽量简化的参考系。同一运动,选择不同参考
系,对运动描述不同。
常用坐标系包括:直角坐标系(由三条标有刻度并相互垂直相交于坐标原点的坐标轴构成)、平面极坐标系、自然坐标系等;(坐标系为参考系的数学抽象)
二、描述质点运动的物理量
2.1、时间和时刻
时间:表示一个过程对应的时间间隔,国际单位制(SI)七个基本物理量之一。时间具有单方向性标量,单位是s(秒);
时刻:某一个瞬时;
质点运动时质点位置与时刻相对于,质点经过的路程与时间相对应。
2.2、位置矢量
定义:质点P在任意时刻的位置,可用从原点O到点P所引的有向线段来表示,用矢量
来代表,这个矢量下就称为质点P的位置矢量,简称位矢。
位矢包含两方面信息:质点P相对参考系固定点O的方位;质点P相对参考系固定点O的距离大小。
特点:(1)矢量性:具有大小、方向加法遵从平行四边形法则(行四边形,这个平行四边形的对角线就表示合向量的大小和方向);
质点在运动,则对应位置也在变化,位置矢量随时间变化。位置矢量是时间的函数。表示为:
上式称为质点运动的轨道参量方程,即质点运动学方程,给出了质点运动的轨迹,也给出了质点在任意时刻的位置。
位置矢量的直角系解析表达式:

,其中i,j,k为常矢量
位置矢量大小:
:位矢与x轴的夹角
:位矢与y 轴的夹角
:位矢与z 轴的夹角
三个夹角之间存在以下关系:
2.3、运动函数(方程)、位移和路程
(1)运动函数(方程):质点坐标随时间变化的函数关系

注意:运动方程是指位置随时间的变化关系;轨道方程式指坐标之间的变化关系,数学表达式为:,一般不含t。
(2)位移:从质点初始位置到终止位置的有向线段(末时刻的位失减去初时刻的位失)

单位:米
位移在直角坐标系中的表示:
位移的大小:
位移的方向:,
为位移与x轴的夹角
位移是矢量,既表示质点位置变更的大小(点4与点B之间的距离),又表示这种变更的方向(点B相对于点A的方位)
(3)路程:路程△s是一定时间内物体所经过路线的总长度。

位移是矢量,路程是标量
表示位移的大小,
表示位矢模的增量,如下图:

2.4、速度和速率
(1)平均速度:位置矢量对时间的平均变化率(位移与发生这段位移的时间之比)
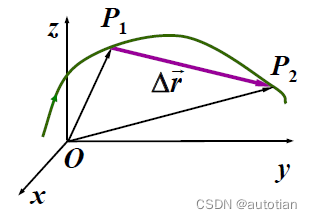
方向:与一致
单位:m/s
平均速度对于位置快慢变化的描述比较初略。如一个物体从原点出发运动一段时间后返回原点,其平均速度为0,此外,弹簧一段时间内的往返运动平均速度也无法很好的表示,但平均速度是向精确描述质点运动快慢的桥梁。
(2)瞬时速度:平均速度在趋近于0时刻的极限(运动函数对时间的变化率)(简称为速度)
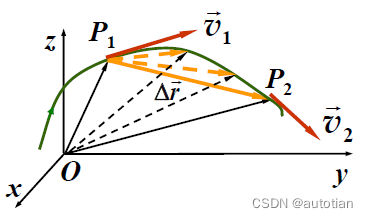
单位:m/s
方向:沿该时刻质点所在处轨道的切线方向,指向运动的前方。
(3)速率():速度的大小叫做速率,质点的速率等于其通过路程对时间的变化率。

无线小时间内位移的大小,而无线小时间内位移和路程的大小是相等的,故
(4)直角坐标系中的速度
直角坐标系下:(i,j,k为常矢量不随质点运动发生变化,因此,对r求导时仅需要对x,y,z进行求导即可)
速度是各分速度的矢量和。
速率:
作用:精确地描述质点运动的快慢;
特点:矢量性(遵循平行四边形法则)、相对性(不同参照系速度不同)、瞬时性(某一时刻)。
例:一质点在XY平面内,依规律,
作曲线运动。求:
1)质点在t =2s到t = 4s时间间隔内的位移;
2)质点在t = 2s到t = 4s时间间隔内的平均速度;
3)质点在t = 2s时的速度
解:1)
是轨道方程,
,可得运动方程为:
,进而可得,一段时间内的位移公式为:
2)平均速度:
3)t=2s时的速度
2.5、加速度
(1)平均加速度
质点末态的速度减去初态的速度除以这段时间的时间间隔为这个质点的平均加速度。

定义:
方向:沿()速度增量的方向。单位:
反映了速度变化的平均快慢
(2)瞬时加速度(加速度)
令,平均加速度的极限即为瞬时加速度
单位:
加速度反应了速度变化的快慢。
(3)直角坐标系
例:一质点在xy平面内运动,轨迹为抛物线,运动方程为:
,
。求:
时(t>0)质点的速度、速率和加速度。

解:
2.6、极坐标系
极坐标系:坐标原点为O,自O点的射线Ox,称为极轴,为位置矢量。
位置矢量与极轴的夹角θ,称为辐角。
规定:自极轴逆时针转至位矢的辐角为正,反之为负。
单位矢量:径向单位矢量;
横向单位矢量,指向θ 增加的方向。

质点的坐标
r :OP,质点到坐标原点的距离,叫做质点的矢径。
注意:的方向随质点位置的变化而变化;直角坐标系中,单位矢量的方向不变。如下图:

质点的位矢:
质点的运动方程:
(1)极坐标系下的速度表示
由质点的位矢,对时间求导可以得到质点的速度:
在t->0时,可得质点在dt内的运动如下图:

将变换前后的坐标系原点平移重合可以得到下图:

由于dt时间很小,故同为一个很小的值,故其大小可近似为
;同样,由于
为一个很小的值,故
的方向可认为近似垂直于
,即为
的方向。可得:
再结合角速度至线速度转换公式,即v=wr,可得到极坐标系下的速度公式为:
其中,为径向速度,
为横向速度。(当为圆周运动时,由于r不发生变化,故速度的第一项为0)
(2)极坐标系下的加速度表示
2.7、相对运动

给定两个坐标系分别为xOy和xO'y,初始时刻两坐标系重合,且有一物体由初始位置P经一段时间运动后到达了位置B,其相对坐标系xOy的位移,可表示为物体相对坐标系xO'y的位移加上xO'y相对xOy的位移,可表示为:
(S坐标系下观察到的速度=S'坐标系下观察到的速度+S'相对S的运动速度u)
(1)相对速度表达式
伽利略速度变换:
,也可写为:
(质点p在S中观察到的速度=质点在S'中观察到的速度+在S系中观察到的S'中的速度)
(2)相对加速度
注意:
1)以上相对运动结论是在绝对时空观下得出的(绝对时空观只在速度u << c 光速时才成立):
只有假定“长度的测量不依赖于参考系”(空间的绝对性),才能给出位移关系式:
只有假定“时间的测量不依赖于参考系”(时间的绝对性),才能进一步给出关系式
和
2)不可将速度合成与分解和伽利略速度变换关系相混淆
速度合成是在一个参考系中,总能成立;
伽利略速度变换则应用于两个参考系之间,只在u << c 时成立;
3)只适用于相对运动为平动的情形
例:一人骑车向东而行,当速度为10 m/s时感到有南风,速度增加到15 m/s 时,感到有东南风。已知风速是不变的,求风的速度。
解:根据题意可绘制下图

所求风对地的速度,根据伽利略速度变换,可分解为人对地的速度和风对人的速度两部分,故
2.8、匀加速运动
英文:Motion with constant acceleration
为常矢量。设初始条件:t = 0时的位矢和速度分别为
,速度和加速度的关系可表示为:
直角坐标系下存在:
(1)匀加速直线运动的直角坐标系表示
匀加速下的运动方程:
由以上可得:
直角系可表示为:
(2)匀加速直线运动
定义:为常矢量,和
在一条直线上
只用一维描述:
若,则存在:
(3)抛体运动——典型的匀加速运动
物体所受加速度:

注意:当抛射角等于90度则为竖直上抛,等于-90度为竖直下抛,抛射角为0则为平抛
抛体运动分析:
1)初始条件:
2)位失:
3)速度:
,x方向为匀速直线运动,y方向为匀加速直线运动
轨道方程:
——抛物线
4)时间
令y=0,可解得物体运动时间
5)射程和射高
射程:
射高:
2.9、圆周运动
质点的运动轨道为圆(任意时刻,质点距离圆心的距离均相同,为半径r,因此常用角度表示圆周运动,角度相关的量称为角量)
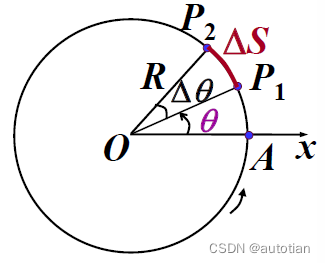

(1)角速度与角加速度
1)角速度
大小:
单位:rad/s
方向:右手法则(四指弯曲运动方向,拇指指向角速度方向)(角速度方向总是和旋转所在的圆是垂直的)
角速度与线速度关系:(线速度方向和角速度方向垂直)
(其中角度单位为弧度,弧长公式弧长=圆心角弧度x半径)
2)角加速度
定义:
单位:
3)法向加速度(向心加速度)
匀速圆周运动的法向(向心)加速度(Normal Acceleration)

如上图,当角度变换值时间变化取极限趋近于0的时候,角度变化值也趋近于0。此时,垂直与线速度方向,由此可得
法向加速度:垂直于速度方向,沿半径指向圆心,沿轨道的法线方向;

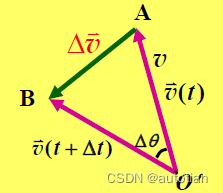
加速度计算为速度对时间的变化率,可写为:
其大小为,速度速率对时间求极限
由于在圆周运动过程中,速度大小并不发生变化,故为等腰三角形,基于三角运算可得:
又,在时间趋于0时求极限,,故
法向加速度大小可计算为:
法向加速度描述了速度方向变化的快慢情况
垂直于速度方向,沿半径指向圆心,沿轨道的法线方向。
2.10、变速圆周运动
(1)变速圆周运动加速度分析
当一个质点进行变速圆周运动时,与匀速圆周运动分析类似,可将其速度变换画为下图:
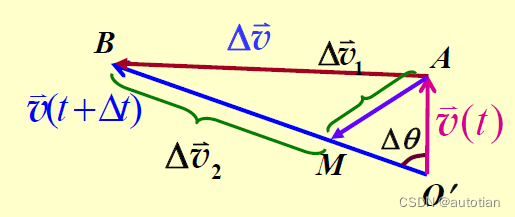
O'M为与下一时刻速度O'B方向一致,大小与O'A相等的向量,则构成O'AM的等腰三角形。如图,变化的速度可表示我向量AM和MB之和。对其求和即可得到变速圆周运动的加速度:
其中,由产生的加速度即为向心加速度
。当时间趋于0时,角度变化
趋于0,则
指向切线方向,故称其为切向加速度((Tangential Acceleration)),又由于
的大小等于下一时刻速率与此时刻速率之差,可得切向加速度大小:
(v为速率)
方向:轨道的切线方向,以速度方向为正向;时,速率随时间增大,方向与速度同;
,速率随时间减小,方向与速度反。
(2)做圆周运动质点的加速度矢量表达式

,
,
,
,
。
其中,为轨道内法向的单位矢量,
轨道切向的单位矢量沿速度方向。
例:如图, 质点沿圆顺时针运动,对于图中的4 种情形,以下说法正确的是

A. 情形1中,质点的运动速率在减小; B. 情形2中,质点的运动速率恒定;C. 情形3中,质点的运动速率在减小;D. 情形4 不存在
正确答案:A.B.D
三、常见的力
3.1、惯性、质量、动量
(1)惯性
定义:物体保持原来运动状态的性质
实验:伽利略斜面实验

如上图,在第一组中,从一个斜坡释放一个小球,并在对面放置一个相同的斜面,小球经过一段时间运动后将到达与起始相近的高度(存在摩擦力的作用);第二组中,对面放置一个斜度更小的斜面,经过更长距离运动后,仍到达与起始相近的斜面高度上;第三组中,撤掉对面的斜坡,为一个平面,若不存在摩擦力,小球将一直运动下去。
伽利略推测,若将物体上所受的力全部撤掉,物体将保存原有运动不变。即,力不是维持物体运动的原因,物体本身具备保存原来运动状态的性质。
(2)质量
质量引入以量度物体的惯性;
实验:以相同的力作用于相同体积的铅块和木块

可以观察到,施加不同力作用在铅块和木块上,其加速度不同,但加速度的比值始终为一个常量。并通过实验我们知道,施加力铅块的加速度相较木块小,其惯性更大。故定义加速度之比等于他们质量的反比:
,可得:
已知,再测出
和a ,便可确定m.
千克标准原器:(一千克)

单位:千克(kg)
经典力学中,质量m与物体的运动状态和参照系的选择无关
相对论中:
(3)动量
定义:质点的动量为,方向与速度方向一致;
单位:千克·米/秒(kg·m/s )

质点系的动量:
3.2、牛顿运动定律
(1)牛顿第一定律——惯性定律
定律:任何物体,如果没有力作用在它上面,都将保持其速度。静止的仍然静止,运动的将做匀速直线运动。
- 给出了物体惯性和力之间的关系:物体具有惯性(保持运动状态或抵抗运动变化),力(改变运动状态)
- 定义了惯性参考系(牛顿第一定律成立的参照系,由实验确定):地面参考系、地心参考系、太阳参考系——相对惯性系做匀速直线运动的参照系是惯性系
- 合力为零
(2)牛顿第二定律
定律:质点的加速度与它所受合力的方向相同,加速度的大小与它的质量成反比,与它所受合力的大小成正比,数学表达式为:
或表述为:物体的动量对时间的变化率与所受的外力成正比,并且发生在外力的方向上。
需注意的是:
指的是合力;
-
只适用于惯性系
-
直角系中:
-
平面曲线运动,沿轨道的法向和切向分解:
(v为速率)
(3)牛顿第三定律(作用力与反作用于定律)
物体间的作用力成对出现。如果物体1对物体2有力的作用,那么物体2对物体1也会有力的作用。两者大小相等,方向相反,沿一条直线。
通常称为作用力与反作用力。同时出现&同时消失,作用在两个物体之上。
只适用于惯性参考系。
3.3、力学相对性原理
对于两个参考系S、S' ,S‘相对S做匀速直线运动,根据伽利略速度公式可得:
(在S’和S中的运动定律是一样的)

任一力学规律在所有惯性系中形式相同
如:动量守恒定律:
S系中:(等式左侧为初始两个物体碰撞前动量和,等式右侧为碰撞后的动量和)
令上式每个速度均减去u,显然在上式成立下,下式同成立:
速度减去u,可视为两个物体S‘系中的速度,即:
,因此可得在S’下动量守恒原理也是成立的。
由上例,可得
力学相对性原理(伽利略相对性原理):任一力学规律在所有惯性系中均相同。从力学观点看,所有惯性系都是等价的;没有哪个参照系更优越。(爱因斯坦后提出相对性原理:任何一个物理规律,在所有惯性参考系中形式都是相同的)。
3.4、万有引力
(1)万有引力定律和引力常量
定律:万有引力定律又称平方反比定律,由牛顿提出,描述两个质点间的引力:
其中,G万有引力常量(100年后由卡文迪许扭秤实验测得),。
需注意的是:
1)万有引力定律适用两个质点,不直接适用于两个有限大的物体

如图,计算A物体对B物体的万有引力,需先将A物体和B物体划分为许多小的质元,分别计算物体A各个质元对B物体某个质元万有引力的合力,再将A物体对B物体所有质量点万有引力进行累加获得A物体对B物体的万有引力。
2)可直接应用公式计算的特例
a. 两个均匀球体间的万有引力可用此公式计算。即m1和m2分别为两个球体的质量,r为两个球体之间的距离;
b. 质量均匀分布的球壳对质点的引力。质点在球壳内,所受引力为零。质点在球壳外,引力可直接用此公式计算;

c. 质量均匀分布的球体对质点的引力。质点m位于球内距球心r 处可直接用公式,但是M为半径r 以内的质量M内,与外面的质量无关。质点位于球外,可直接使用公式。
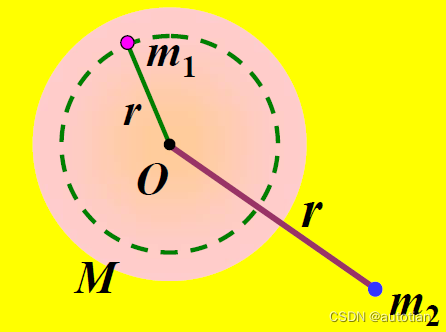
(2)引力质量和弱等效原理
定义:
称和
为引力质量,其中
和
,分别为
和
距离相同距离点A产生的万有引力,即对相同等距离物体万有引力之比等于质量之比。
引力质量量度了这个物体与其他物体相互吸引的性质。
实验验证: 牛顿用单摆,厄阜用扭秤,迪克等的改进实验.
弱等效原理(常常简述为惯性质量等于引力质量):惯性质量与引力质量成正比,适当的选择单位可使两者相等。
爱因斯坦在此基础上提出了等效原理——加速度和引力是等效的,从等效原理出发提出了广义相对论。
(3)万有引力例题
例::一水平放置的均匀细棒AB长为L,质量为M。如图所示,在其延长线上距A端d 处有一个质量为m0 的质点P,求:细棒与质点P 间引力的大小。
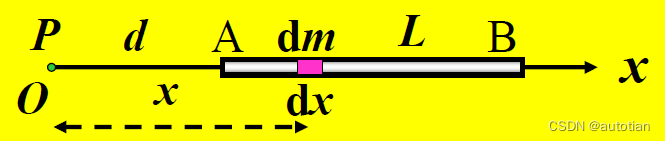
解:设细棒的线密度(单位长度质量)为λ 。因质量均匀分布,故
质点受到的引力为:
质点受到细棒的引力为计算细棒各质元对质点的引力积分:
当细棒的长度远小于细棒与质点之间的距离时,存在:
与平方反比定律一致。
3.5、重力
将一个物体从空中释放,物体会做自由落体运动落到地面,同时我们可以观察到一种现象同一点释放物体的加速度均相同。这时由于物体受到重力的作用。由重力产生的加速度我们称为重力加速度。
重力:
方向竖直向下,其中m为物体的质量,g为重力加速度,一般取
重力源自物体与地球之间的万有引力,若忽略地球自转,并设地球为半径为R 的球体,可计算:
其中,M为地球的质量,两边同时消去物体的质量m,可以得到:
需注意的是,地球是一个椭球体。因此物体重力加速度g并非一个常量而是与它所在地面高
度和地理维度相关,并非常数。
3.6、电磁力
物体因带上电荷所受到力称为电力,运动电荷与运动电荷之间的作用力称为磁力。

如图,两个正负电荷之间的作用力为电力,两块磁铁之间的作用力为磁力。
电场力、重力、万有引力都有一个特点,相互作用的物体不需要接触就可以有力的作用,是通过场来传递,电磁力是通过电磁场来传递,重力和万有引力是通过引力场来传递。
3.7、点接触力(弹簧弹力、拉力与张力)
接触力:必须接触才会有的力;
弹簧的弹力和绳子拉了和张力都是作用于一点,称这种接触力为点接触力。
(1)弹簧的弹力

将小球连接弹簧,起始时出于静止位置,当我们沿x轴正向拉动小球,小球受到弹簧来自x轴负向的力;而当我们沿x轴负向推动小球,小球受到弹簧来自x轴正向的力。
弹簧的弹力遵循胡可定理,即在弹性限度内:
其中, k为弹性系数,又称劲度系数也;x偏离静止位置坐标原点的位移,即为弹簧的形变量。
(2)拉力和张力

如图,一根绳子上端固定在天花板,下端固定物体,绳子发生变形,对下面的物体产生拉力,拉力方向竖直向上。绳子各个段之间也会有力的作用,绳子不能看作质点。
接下来,我们将绳子划分为三段,如图:

我们记绳子右端拉力,左端拉力为
。对于划分后的中间段绳子,我们记右端的张力为
,左端张力为
。对于左右两端的绳子,所受拉力和张力的关系如下:
对于左右两端的绳子, 拉力和张力是一对作用力与反作用力,设绳子水平向右运动,对于加速运动的绳子ab两端的张力一般是不相等的,对于一根轻绳,其质量可视为0,在此下,可得两端受力相等。故轻绳中各处张力相等。
3.8、面接触力(正压力、支持力、摩擦力)
物体与斜坡的接触不是在一个点上,而是在一个面上,我们称为面接触力。

如上图,将一个物体放置在斜坡上,斜坡对物体产生垂直向上的力称为支持力;物体对斜坡产生垂直向下的反作用力称为正压力。
当物体在斜面上时,由于表面之间不光滑,因此在相对移动或者相对运动趋势的时候彼此之间产生摩擦力,在面接触下,摩擦力可分为滑动摩擦力和静摩擦力。
(1)滑动摩擦力(sliding friction)
其中,为滑动摩擦系数,N为支持力。其方向与物体运动方向相反。
(2)静摩擦力(Static friction)

如图,将质量为m的物体静置在斜坡上,物体重力存在沿斜坡向下的分力,大小为。又由于物体处于静止状态,重力沿斜坡向下的分力与摩擦力是一对作用力与反作用力,大小相等,方向相反。其最大静摩擦力为:
其中,为静摩擦系数,静摩擦力方向与相对运动趋势的方向相反。
一般来说:
对于人跑步时,若没有与地面打滑,人向前的力即为静摩擦力所提供。
(3)不同材料之间的摩擦系数

表面越光滑摩擦系数越小,摩擦力也越小;摩擦力一般来讲是由于相互接触之间是凹凸不平的,由于表面之间不光滑,因此在相对移动或者相对运动趋势的时候彼此之间产生摩擦力表面越光滑摩擦力越小(相对的);
如果两个物体表面光洁度非常高,两个物体放在一起,摩擦力会非常大,不遵守动静摩擦公式,这是因为如果物体表面光洁度非常高,两个物体放在一起时,它们之间分子会产生引力的作用(分之间作用力需使分子间距离在百万分之一厘米的范围之内)。
3.9、流体阻力
流体:气体和液体没有固定的形状,很容易流动,统一称为流体。
在流体中运动时,会受到流体的阻力。流体对物体产生的力,与物体运动的方向相反,因此称为阻力。
流体阻力:方向与物体在流体中的运动方向相反;大小与物体在流体中的运动速度相关,速度越大,阻力越大;阻力大小还与物体的横截面积、物体的形状以及流体的性质有关。
例:人在水中游泳受到水对人的阻力;高铁运行中,空气阻力是必须要考虑的一项受力。


上图分别为莱特兄弟的第一架飞机和现代飞机照片。可见早期飞机不是流行性,人们不断提高飞机的速度。人们发现当飞机速度达到飞机的升速时,常会不明原因的爆炸,后来经过研究发现这是由于空气阻力引起的。改进飞机的一个方法就是改进飞机的外形,以减小空气阻力。
流体助力的计算:
(1)物体在流体中的运动速率不太高
其中,v为物体在流体中的运动速度;k为比例系数,与物体的大小、形状和流体的性质相关。
(2)若物体在流体中的运动速率较高
物体在流体中运动速率较高时,会使流体中出现漩涡,此时与物体的速度平方成正比
其中,b为比例系数,与物体的大小、形状和流体的性质相关。
如果物体在流体中的速度再提高,物体受到的流体阻力还会极速提高。
(3)终极速率(收尾速率)
物体在流体中的下落,若,其中v为下落的速率,f为流体向上的阻力。物体下落时受力存在以下等式:
加速度为零时, 物体的速率达到终极速
终极速率是物体在流体中下落的最大速率,又称为收尾速率。
终极速率与质量和比例系数b相关,设计降落伞时可以尽量增大b,设计飞机时应尽量减小b。
例题:在液体中由静止释放一质量为m的小球,它在下沉时受到的液体阻力为。设小球的终极速率为
,求:t 时刻小球的速率。

解:在液体中,小球受重力作用向下运动,其受到向下的重力,向上的浮力,以及与运动方向相反的流体阻力,可列等式:
达到终极速率时:
两式联立可得:
又初始条件为t=0时,速度为0,故
,
3.10、基本的自然力
所有的力都可以归于四种基本的相互作用:这四种相互作用分别为:
- 万有引力相互作用The gravitational Force (天体之间的主要受力,借助万有引力探索宇宙)
- 电磁相互作用The electromagnetic force (存在于静止的以及运动的电荷之间,弹力、摩擦力流体阻力都起源于电磁相互作用)
- 强相互作用The strong nuclear force(存在于质子、中子等粒子之间,原子核是由质子和中子构成,质子带整电,之间存在库伦斥力的相互作用,正由于强相互作用才使它们凝聚为一个原子核;此外,强相互作用还使夸克束缚在一起,形成了质子和中子)
- 弱相互作用The weak nuclear force (主要表现在粒子的衰变过程中,制约着放射性现象)
四种相互作用的有效范围和强度:

由表中数据可知,力程最短的为弱相互作用。
对于强相互作用,若两个粒子之间距离非常远,强相互作用可以忽略不计;若两个粒子之间的距离逐步缩小,小到米时,强相互作用将表现出主导作用,并表现出来的是引力;若两个粒子之间的距离进一步减小,减小到大约0.4x
时,强相互作用表现为斥力。
对于表中强度,取一对质子计算,两者中心的距离等于它们的直径。
根据现代理论,传递强相互作用的是胶子,传递电磁相互作用的是光子,传递弱相互作用的是中间玻色子,传递万有引力相互作用假定为引力子。
3.11、牛顿运动定律的应用
牛顿运动定律的解题步骤:
- 选定对象,隔离物体
- 受力分析,画示力图
- 分析运动
- 选坐标系,列方程, 求解未知量
- 检验与讨论
例:物体A,质量为m,通过不可伸长的轻绳,跨过光滑的轻定滑轮与弹性系数为k的水平轻弹簧相联。当弹簧为自然伸长时,将A 从静止释放。求: 下落过程中,A落下x 距离时的加速度和速度。

解:以A为研究对象,设A下落的距离为x,由于绳子是不可伸长的,因此A下落的距离就是弹簧的伸长量。对于物体A,受到向下的重力mg的作用,还受到向上T=kx绳子拉力的作用。
物体为做竖直向下的运动,建立坐标,坐标原点为物体的初始位置,按照牛顿第二定律,可以得到:
这里要求得x和速度v之间的关系,因此列等式:
将上两式联立,可得:
结合,x=0,v=0的初始条件,可得:
,
例:一根不可伸长的轻绳,跨过固定在O点的光滑轻滑轮,两端各系一个小球。a 球放在地面上,b 球被拉到水平位置,且绳刚好伸直,然后将b球自静止释放。设两球质量相同,求:(1) b 球下摆到与竖直线成θ角时的速率v(a 未离开地面)。(2) θ=? 时a刚好离开地面
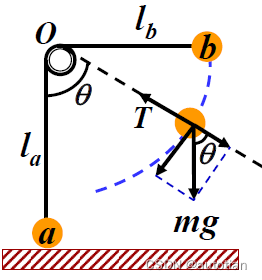
解: (1)以b球为研究对象
b球受到绳子的拉力,方向沿着绳子;受到竖直向下重力的作用。
b球在下摆过程中,a球一直没有离开地面,因此,b球绳长一直不变,走一段圆弧。为一个平面曲线运动,一般方法为,将力沿着曲线切向和法向分解,可列方程:
初始时刻,水平放置,故角度为90度,速度为0
(2)θ=? 时a刚好离开地面

选择a求为研究对象;
a求受到向下的重力,a求与地面接触会受到地面向上的支持力,还会受到绳子向上的拉力;
a求一直静止在地面上,合力为0.由于为轻绳和轻滑轮,故绳子对a和b的拉力是相等的。因此,可列方程:
T= mg 时,a刚好离开地面
3.12、非惯性系与惯性力

上图中,车内地板放置一物块,假设地板是光滑的。
观察者先在地面上观察物块运动,某一时刻,车开始以a为加速度,加速向前运动,物块因保持原有静止的惯性向后滑动(地面光滑,物块在水平方向所受合力为0),车厢加速向前运动。相对车厢物块为向后滑动。
观察者站在车厢内部对物块进行观察,地面为惯性系,则加速的车厢为非惯性系。再次观察时,物块所受合力为0,汽车加速运行时,人观察到,物块突然有了向后的加速度a,因此得出结论,牛顿第二定律在这样的车厢中是不成立的。
在惯性系中,牛顿运动定律是成立的;在非惯性系中,牛顿运动定律并不成立。
近似惯性系:

惯性系是非常少见的,非惯性系是非常常见的。
(1)直线加速参照系
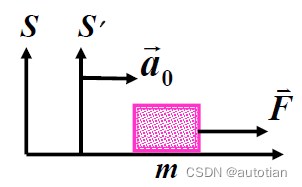
设S 为惯性系,S ' 为非惯性系 。S '相对S做直线加速运动,加速度为。
现考虑一物体,质量为m,所受的合力为F,设物块相对于S系的加速度为a,相对于S'的加速度为a'。
两个平动参考系之间,加速度变换:
在 S 系,对于质点 m:
不随参考系变化:
可得在 S′ 系中,因此牛顿第二定律在非惯性系不成立。
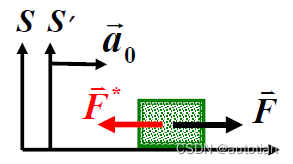
在上述分析计算中, 与惯性系下多了一项
惯性力:为一种假象的力,称为惯性力。惯性力的大小为
,即为物体的质量乘上S'相对S的加速度;惯性力方向与
方向相反。
将惯性力记入物体所受合力之中,物体除了所受真实力F之外,还受到假象的力F*,即在非惯性系中:
牛顿第二定律形式上成立。
需注意的是惯性力为一种假象的力,一种不存在的力,惯性力不是相互作用,不存在反作用力。
例:一匀加速运动的车厢内,观察单摆,平衡位置如何变化? (加速度a0 ,方向如图,摆长l ,质量m)

解:在S'系中观察小球的受力情况,可知小球受到与加速度方向相反,即向左的惯性力,同时受到向下的重力。重力与惯性力组成的合力与绳子对小球的拉力是一对平衡力,因此:
在平衡位置:
(2)转动参照系——惯性离心力
若参照系处于转动状态,则参照系为非惯性参照系。考虑以下情景:

人静止地面不懂,一个圆盘以角速度进行转动,圆盘上静置一个物体,物体质量为m,向量
为圆心指向物体的向量,长度为圆心到物体中心之间的距离。在物体随着圆盘进行转动时,受到圆盘给物体的静摩擦力,且静摩擦力与向心力是一对平衡力。
地面参照系S 中,质点m圆周运动,向心加速度为:
静摩擦力为:(与向量
的方向相反)
为了能够在S'观察分析物体的受力运动情况,引入惯性离心力:
在转盘参照系S′ (非惯性系)中,质点m受摩擦力,但是静止。
惯性离心力:,大小为
,方向为离心方向。由于同为惯性力,是一种假想的力,故无反作用力。
引入惯性离心力后,在S′ 系中有:
例:质量为m 的物体静止在以匀角速度ω 转动的圆盘上,距离圆盘中心的距离为r,如图。设物体与圆盘间的静摩擦系数为μ,欲使物块与圆盘间不出现相对滑动,ω 的最大值是多少?
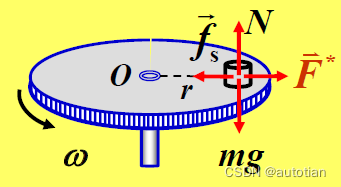
解:以转盘为参照系,物块静止在转盘上,受到圆盘对物块的精摩擦力,此外,还受到惯性离心力,这两个力是一对平衡力。
竖直方向:,水平方向:
,此外,在水平方向还存在一个与惯性离心力大小相等方向相反的静摩擦力
结合3.8最大静摩擦力可知:
,
,
,
(3)科里奥利力
考虑以下情景,如下图,存在一个圆盘
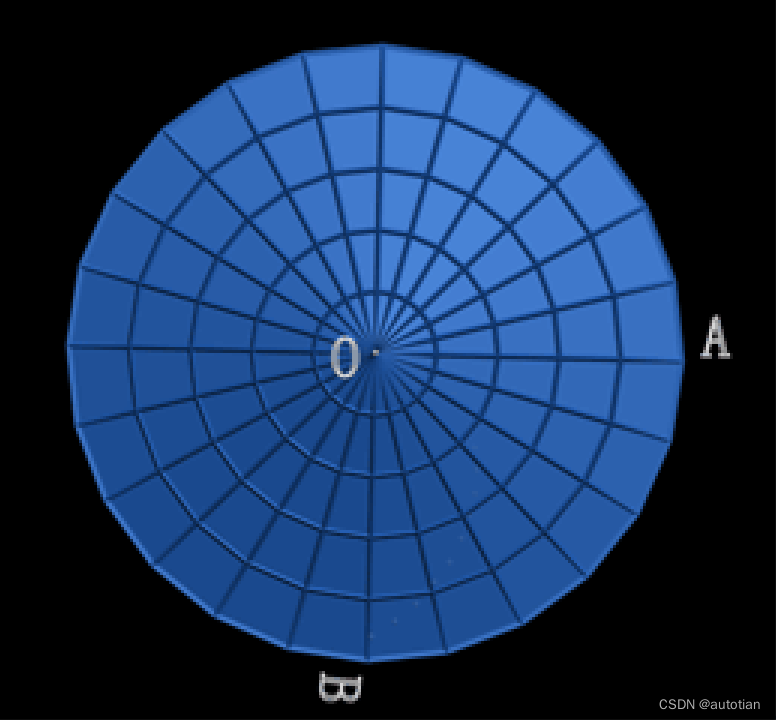
从0点沿0A方向抛出一个小球,当圆盘静止时,站在A点的人可以接收到小球。
当圆盘以一定角速度逆时针转动时,站在A点的人就会观察到,小球会随着圆盘转动而无法接收到了;
当人站在0点观察小球运动,此时转动的圆盘相对人来说是静止的,A点相对0点的人来说同样为静止。此时,同样从0点抛出一个小球,发现小球受到一个垂直速度方向力一样,产生一个垂直于速度方向的加速度,加速偏离0A直线。由此,由法国科学家科里奥利提出了科里奥利效应和科里奥利力。

科里奥利效应: 转动参照系中观察到的运动物体向其侧向偏离的加速现象。
科里奥利力:产生科里奥利效应的虚拟惯性力。
为分析科里奥利力的大小,进行如下实验。设物体m圆盘S'系中光滑的凹槽内,且相对凹槽有速度(即物体相对S'系中的运动),转盘以匀角速度转动。在S'中看m除受惯性离心力外,还附加一个与速度
有关的惯性力。

惯性系S(地面)分析小球受力,小球相对地面存在的转动角速度,所受力为角速度对应的向心力:
在非惯性系(转盘)S′中分析小球运动,小球相对凹槽运动,存在向心加速度:
对比小球在S系和S'系受力分析,可得:,即小球在转动系下运动必然存在虚拟的惯性力:
将其转化为矢量形式:
按矢量形式对S系下标量受力形式分析:,大小为
,其中
为速度v与角度
之间的夹角,方向根据右手定则四指按照角度最小由v转向
角度,大拇指的方向即为叉乘方向。由于圆盘逆时针转动,故角速度方向为垂直向上,四指由v转向
大拇指指向圆心向外方向,与指向圆心的向心力方向相反,故为负号;
中,r由圆心向外,与向心力方向相反,故同为负号。由此可以看到,矢量形式与标量形式大小上相符。
定义惯性力:,其中:
惯性离心力:
科里奥利力:
加入惯性力后,S'中物体的运动仍符合牛顿第二定律:
注:可以证明,一般情况下,在匀速转动参考系S ′ 中, 运动物体除受惯性离心力外,都还要附加一个科里奥利力(Coriolis force),。方向即与v′ 垂直,又与ω 垂直,v'为物体相对S ′系的速度。
此时,再对开始时圆盘实验进行分析:
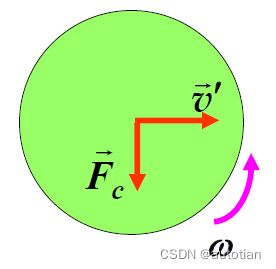
如图,小球受到垂直v'向下的科里奥利力,解释了在S'系中观察到小球加速偏离运动方向的原因。
3.13、牛顿运动定律总结
牛顿第一定律也叫惯性定律,告诉我们物体运动状态发生变化的原因,即物体受到力的作用。如果一个物体不受力的作用,物体将保持原有运动状态不变。
牛顿第二定律给了定量方程,可以利用定量的研究物体运动状态的变化情况。
牛顿第三定量给了我们两个物体之间相互作用的性质,作用力与反作用力大小相等,方向相反,作用在不同的物体上(平衡力,大小相等,方向相反,作用在同一物体上),性质相同的力,同时出现同时消失。

惯性参照系:牛顿第一定律成立的参照系。一个系统是否为惯性参照系,需要由实验来确定,取决于我们的观测精度,常用的惯性参照系是地面参照系、地心参照系和太阳参照系,以上三个参照系中太阳参照系是精度最高的参照系。
非惯性参照系:利用牛顿第二定律的推广进行分析,核心方法为引入惯性力。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










