今天还跟昨天一样,就做了两道题,而且都是通过题解做出来的,自己还是对搜索没有掌握,仅仅能看懂题解而已,自己独立做还是不行。今下午做了一道题,真是醉了。。。照着题解找错误找了一下午没改出来,然后在晚上终于改出来了。。。还有,今下午学了Floyed算法,原理虽然简单,但真要放在题目里还真的不简单。最后贴上这道有毒的题吧:(但我觉得题解非常巧妙啊~~~,用到四色定理,长见识了)
Channel Allocation
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 20000/10000K (Java/Other)
Total Submission(s) : 74 Accepted Submission(s) : 33
Since the radio frequency spectrum is a precious resource, the number of channels required by a given network of repeaters should be minimised. You have to write a program that reads in a description of a repeater network and determines the minimum number of channels required.
2 A: B: 4 A:BC B:ACD C:ABD D:BC 4 A:BCD B:ACD C:ABD D:ABC 0
1 channel needed. 3 channels needed. 4 channels needed.
题意:
当一个广播电台在一个非常大的地区,广播站会用中继器来转播信号以使得每一个接收器都能接收到一个强烈的信号。然而,每个中继器必须慎重选择使用,使相邻的中继器不互相干扰。如果相邻的中继器使用不同的频道,那么就不会相互干扰。
由于无线电频道是一有限的,一个给定的网络所需的中继频道数目应减至最低。编写一个程序,读取一个中继网络,然后求出需要的最低的不同频道数。
分析:就是染色问题,给出相邻关系,问最少用几种颜色,保证相邻的不会有重色
有个四色定理,四色定理的本质就是在平面或者球面无法构造五个或者五个以上两两相连的区域,就是给相邻的区域涂颜色,最多用四种颜色(用于剪枝)
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int mp[30][30];
int v[30];
int n,flag;
void dfs(int x)
{int i,j;
if(x==n+1)
{
flag=1;
int maxn=1;
for(i=1;i<=n;i++) maxn=max(v[i],maxn);
if(maxn==1)
{
cout<<"1 channel needed."<<endl;
}
else
{
cout<<maxn<<' '<<"channels needed."<<endl;
}
return ;
}
for(i=1;i<=4;i++)//四色
{
for(j=1;j<=n;j++)
{
if(mp[x][j]&&v[j]==i)//if(mp[x][j] && v[j]==i),就在这一步出错了,把mp[x][j]写成mp[x][i]了
break;
}
if(j==n+1)
{
v[x]=i;
dfs(x+1);
if(flag)
return ;
}
}
}
int main()
{ char str[100];
int l,x,y;
while(cin>>n,n)
{ memset(v,0,sizeof(v));
memset(mp,0,sizeof(mp));
flag=0;
for(int i=0;i<n;i++)
{cin>>str;
l=strlen(str);
x=str[0]-'A'+1;
for(int j=2;j<l;j++)
{
y=str[j]-'A'+1;
mp[x][y]=1;
}
}
dfs(1);
}
return 0;
}
附:
四色定理的“相邻”是指两块多边形地区“至少一条边重合”才为之相邻
“至少一条边重合”同时也隐含了“任意边(线段)不正规相交
如:
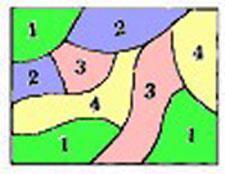
再反观本题的模型,本题的相邻是“两点有边连接,但任意两边不交叉(正规相交)”,这种“相邻”其实就是四色定理的“相邻”。
我举一个例子就一目了然了:
N=7
A:BCDEFG
B:ACDEFG
C:ABD
D:ABCE
E:ABDF
F:ABEG
G:ABF
画成图就是:
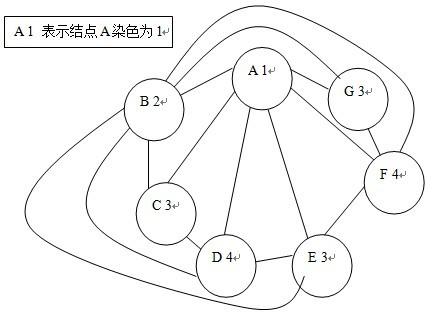
PS:由于边不允许相交,这已经是7个点的最大连接数
四色定理的原始理论依据:
对于一个散点集,若要求尽可能连接任意两个点,但任意一条边边不允许与其他边相交,
那么当散点集的元素个数<=4时,连接所得的图必为一个一个无向完全图
当散点集的元素个数>4时,连接所得的图必不是一个完全图
完全图:任意两点均相邻
最后千万要注意输出,当频道数大于1时,channel为复数channels

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








