数据结构入门--二叉堆

前面的文章中，我们曾提到一种先进先出的数据结构，那就是队列。但现实生活中，我们对“排队”的需求有时并不只是以先后次序为优先标准。比如如果一个医院突然来了一个心脏病突发的患者，当然是要马上优先抢救，总不能让他慢腾腾的排队等着吧？那么为了应对这类情形，就要引入“优先级队列”

优先级队列与普通的队列区别就在于其每个元素都有一个权值，这个权值可以理解为该元素的优先级，优先程度，或者就上面例子而言的患者病情的紧急程度。那么这样你应该明白，优先级队列每次出队列的元素即是队列中权值最大的那个元素，但是注意这里的“最大”并不单纯指数值上的最大，而是代表优先程度

实现优先级队列可以有很多种方式，不就是每次都删除权值最大的元素嘛，用数组遍历下就好了嘛。这是最自然的想法，但是请思考一下，这样每次查找到最值元素需要O(n)的时间，删除后的移动元素又是O(n)级的时间，显然在效率上是很低的。那么，如果是有序数组呢？这样的确可以在常数时间找到最大值，但移动元素仍是O(n)的。那么有序链表总行了吧？有序链表可以使删除元素达到常数的时间，但插入新元素的时间复杂度仍是O(n)的。我们发现简单的顺序结构，无论如何都无法使优先级队列的插入和删除同时突破O(n)的限制

想突破O(n)的界限，根本问题即是将从序列中查找最大值这一过程优化的更快，这就需要借助前面文章提到过的完全二叉树。根据完全二叉树的性质，我们知道一颗完全二叉树按层序编号是与满二叉树一致的

每个完全二叉树最底层缺失的结点仅是最右边一段连续的结点。那么由于这个性质我们完全可以使用数组来表示一颗完全二叉树。
因此现在我们分析优先级队列的实现结构，他在逻辑上是一颗完全二叉树，但在物理结构上，它是一个一维向量。以这种方式实现优先级队列的结构，即是本文真正的主角：二叉堆
二叉堆有两种(有序性)：
最大堆：任意结点的键值均大于其子树所有结点的键值
最小堆：任意结点的键值均小于其子树所有结点的键值
堆的性质：
逻辑上是完全二叉树，物理结构上是一维向量
一个堆的左右子树也分别都是堆
由性质可以知道如果判断一颗树是否为二叉堆，首先要看其是否为一颗完全二叉树，再检查其结点键值是否符合最大/最小堆的特点。这个问题很简单，就不用图片示例做举例了。
那么现在我们给出堆的构造，以便后面的讲解

 ComBinHeap<T>::ComBinHeap(T a[],int n)
{

    elems = new T[MAXSIZE];
    elems[0] = MAXDATA;
    length = 0;
    for (int i = 1, j = 0; j < n; j++, i++)
    {
        this->elems[i] = a[j];
        length++;
    }
    BuildHeap();
}

上述是对堆的初始化，值得说明的一点是elems[0]=MAXDATA这句话，我们在存放堆的向量的0号位置放置了一个哨兵，这个哨兵的值是永远大于堆中任意元素的值，至于为何使用这个后面会讲到

那么对于一个堆，我们最关注的还是它的插入和删除的问题。这里仅以最大堆为例。
既然堆的物理结构是一个线性的数组，那么插入一个元素自然会想把它插入在最后一个位置，而这个位置也即是完全二叉树最后一个结点。

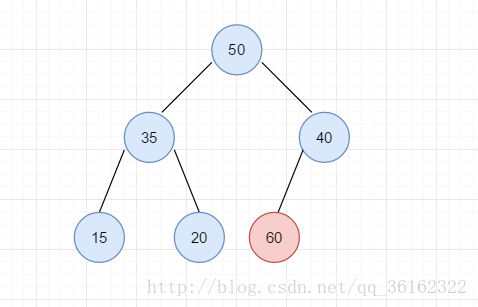
入上图的序列我们在序列中插入60。但这一插入显然破坏了堆的有序性，所以我们从破坏的源头60开始调整，交换40和60

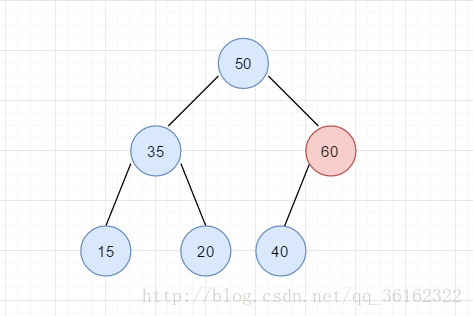
调整后，根节点的右子树现在保证了有序性，是一个堆。但没有结束，我们发现当60上升一层以后，键值仍然比其父结点要大，在新上升的一层仍不满足有序性，因此重复刚才的调整，交换50和60.

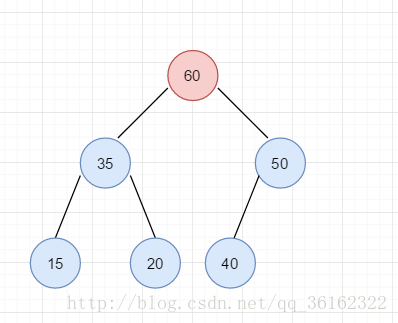
现在60被推到了根结点，此时整棵树就被调整成堆了。我们可以看到整个过程就是在最底层新插入的结点不断向上过滤的过程，我们称这个操作为上滤

那么要如何把这个操作实现为代码呢？每次有序性的破坏，是由于父节点的键值小于孩子结点造成的，所以每次调整要先比较上滤的结点和父节点的大小，发现父节点小了，就父子交换。虽然表面上是交换道理，但实际上我们并不需要频繁的进行交换，而是先用临时变量先将插入的元素存起来然后找到合适的位置再放上

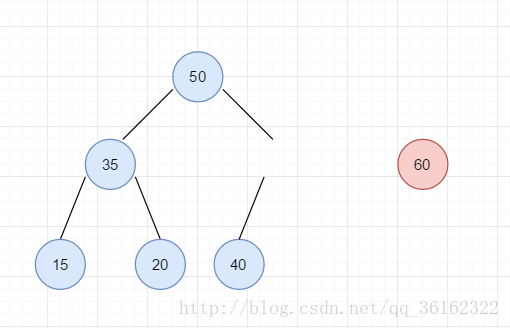
如上图，40比60小，然后40下去。

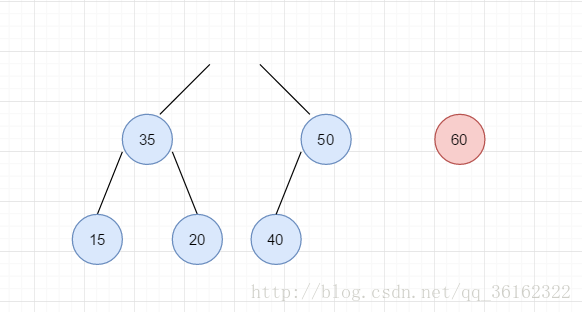
50和60比，依然小，50下去。还记不记得我们最开始在elems[0]的位置放置了一个哨兵？现在60和50比完之后，再向上比自然就是0号位置了，但这个位置是一个无限大的值，因此60的上滤便到此为止，将其放置在1号也就是根节点的位置上。这个哨兵，你当然可以不设置它，但这样会为算法的实现带来点小麻烦。我们知道完全二叉树从1开始编号时，编号为 i 的结点左右孩子分别为 2*i 和 2*i+1,其父亲为 i/2 。但当从0开始编号时，左右孩子就为 2*i+1 和 2*i+2，因此对于父节点的编号，左右孩子是不同的，左孩子是 i/2 ，右孩子是 i/2-1 。这就不得不将情况分开处理。而从1开始编号就将寻找父节点统一为 i/2 。所以根节点就为elems[1]。而空出的elems[0]就作为一个存有极大值的哨兵，就样就无需考虑上滤的结点上滤溢出的情况，因为总有个比它大的值作为哨兵，使得上滤的结点最晚也会停在根节点的位置
下面是插入操作的具体代码，很简单对不对？

void ComBinHeap<T>::Insert(T e)
{
    if (this->length == MAXSIZE) 
    {
        cout << "最大堆已满" << endl;
        return;
    }
    int i = ++this->length;
    for (; elems[i / 2] < e; i /= 2)
    {
        elems[i] = elems[i / 2];    //下滤
    }
    elems[i] = e;
}

刚刚用很久讲完了插入，删除元素原理其实很相似。我们想从线性序列中删除一个元素，同样我们也很自然的想删除最后一个元素，但现在我们要操作的是堆，优先级队列，我们只能删除堆顶(队头)元素。但变通下思考，我们只是从逻辑上删除堆顶结点，就像我们的堆的结构只是逻辑上是棵二叉树一样。我们将堆顶的元素先用临时变量存起来，最后返回。然后删除最后一个结点，并将结点的键值付给堆顶，这样不就做到了逻辑上删除堆顶，物理上删除末尾元素了吗?

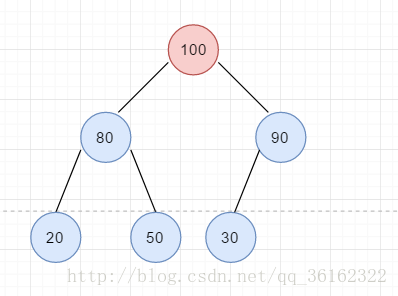
比如我们从上面的堆中删除元素。我们用临时变量存放100等着最后返回，用50替代100成为新堆顶，然后删除结点50

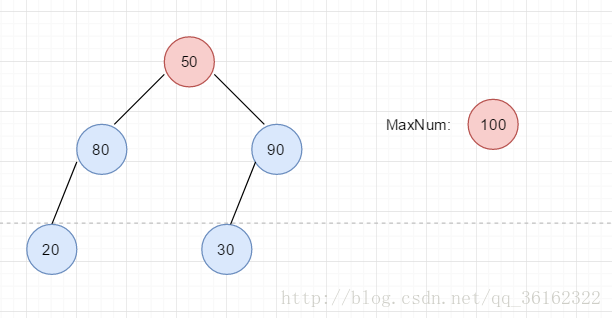
然后现在需要处理的问题就依旧是调整堆的有序性，只不过这次是从上面往下调。与插入时不同的是，每个结点可能有一个或两个孩子，当只有一个孩子时，就正常比较，有两个孩子时，就要用两个孩子中较大的一个比较。

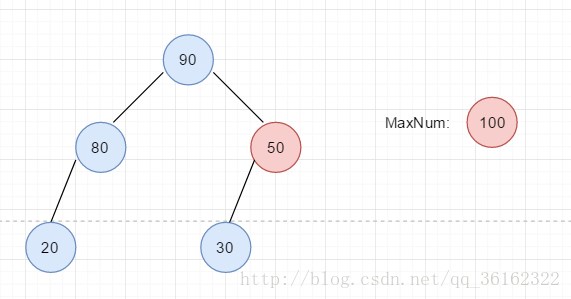
如上图，80和90比，然后50和90比，然后50换到下面，这时整棵树满足堆的特性，调整完毕。这样把根节点层层向下调整的过程，类似的我们称之为下滤
删除的代码要相对长些，因为多了孩子数的判断和孩子间的比较，但下滤的基本原理和上滤是一致的

T ComBinHeap<T>::Delete()
{
    if (IsEmpty())
    {
        cout << "当前堆中没有元素" << endl;
        return -1;
    }
    T maxItem = elems[1];       //保存最大值
    T temp = elems[this->length--]; //取最后一个元素替换第一个元素，然后重新找位置
    int parent, child;
    for (parent = 1; parent * 2 <= this->length; parent = child)
    {
        child = parent * 2;
        if (child != this->length&&elems[child] < elems[child + 1])//temp==length说明没有右孩子
            child++;
        if (temp > elems[child])    
            break;
        else elems[parent] = elems[child];  //下滤
    }
    elems[parent] = temp;
    return maxItem;
}

插入和删除都介绍完了，，但别忘了我们还没有一个堆呢，得建一个才行。对于建堆，依旧是最自然的想法，逐个插入，堆就建成了。。。怎么可能！其实你当然可以这么做，但想一下，一次插入操作，结点逐层上滤的次数显然和树的高度有关，也就是O(logn)级的，那么插进n个结点整体的时间复杂度也就是O(n*logn)级的。但实际上，建堆的过程是可以在线性复杂度下实现的。
回顾刚刚讲过的删除操作，我们用最后一个元素替代堆顶元素，将问题化成左右子树均为堆的情况下，根节点破坏有序性。也就是说，先使其满足完全二叉树的结构性，再去调整有序性。堆的建立过程依然使用这个思想，这也就是为何要在最后讲建堆。
我们拿到一个序列，第一步要先将序列的值全部赋给完全二叉树的结点，先使其满足结构性。接下来从最后一个结点的父节点开始，逐层，一个一个的调整子树。如下图的完全二叉树

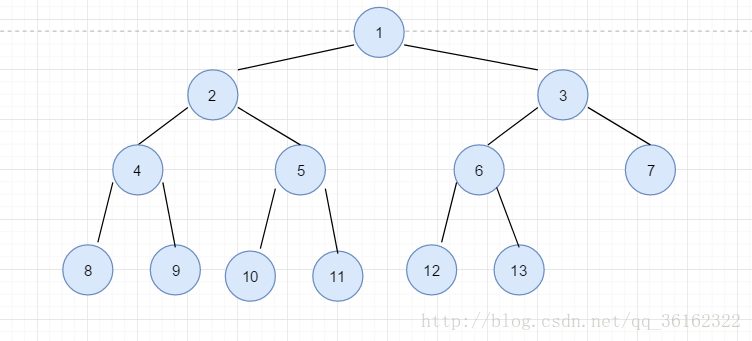
使它调整为堆，首先看最后一个结点的父节点也就是6，它的左右子树均为堆，但6破坏了当前子树的结构性，所以交换6和13。继续往前，结点5,4也是一样的操作。我们发现这样的操作，和删除中最后结点替换根节点后进行的下滤操作一致，只是对象从整个树变为一个个的小子树。我们从高度为2的子树开始逐渐将子树调整成堆，然后递归向上再重复下滤的操作。具体调整流程就不具体图示了，下图将给出上面的调整结果，看看你有没有调对呢？

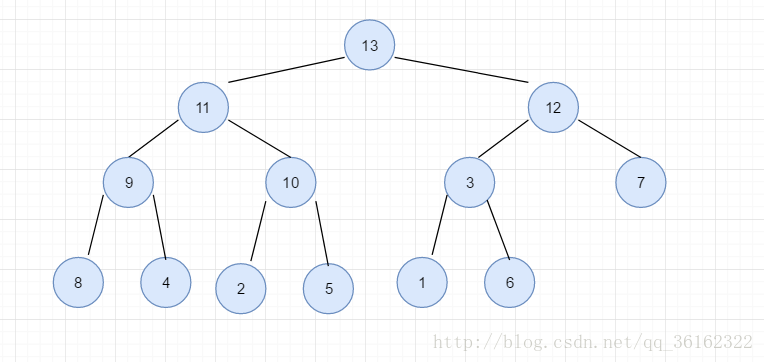
下面是建堆的具体代码实现：

void ComBinHeap<T>::BuildHeap()
{
    for (int i = this->length / 2; i > 0; i--)
    {
        int parent, child;
        T temp = elems[i];
        /*与删除时的下滤操作基本一致*/
        for (parent = i; parent * 2 <= this->length; parent = child)
        {
            child = parent * 2;
            if (child != this->length&&elems[child] < elems[child + 1])
                child++;
            if (temp > elems[child])
                break;
            else elems[parent] = elems[child];
        }
        elems[parent] = temp;
    }
}

代码的总体思路就是从最后一个结点的父亲开始，往前逐个结点下滤直到根节点下滤完毕，整个堆就建成了，其整体复杂度是线性的

堆的应用其实不仅是用来实现优先级队列，堆的意义在于它用O(logn)级别的时间来在无序序列中查找最值，因此凡是需要频繁查找最值的算法都可应用堆的特性