逆元粗解

最新推荐文章于 2021-07-19 15:32:10 发布

「已注销」

最新推荐文章于 2021-07-19 15:32:10 发布

阅读量254

点赞数

文章标签：组合数

本文链接：https://blog.csdn.net/qq_36172950/article/details/76046038

版权

逆元定义：对于正整数和，如果有，那么把这个同余方程中的最小正整数解叫做模的逆元。

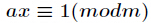
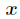
逆元的求法，包括费马小定理跟拓展欧几里得两种。

费马小定理：

int C[n];
long long pow_w(long long a,long long b,long long c)
{
    long long ret = 1;
    while(b)
    {
        if(b&1)ret = (ret*a)%c;
        a = (a*a)%c;
        b>>=1;
    }
    return ret;
}

void init(int t){  //求t时间时的逆序数
    C[0] = 1;  
    for(int i = 1; i <= t; ++i){  
        C[i] = C[i - 1] * (t - i + 1) % mod *pow_w(i, mod - 2,mod) % mod;  
    }
//求单个逆序数时直接用
//int inv2 = power_mod(a, mod - 2, mod);

拓展欧几里得：

ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if (b == 0)
    {
        x = 1;
        y = 0;
        return a;
    }
    ll r = exgcd(b, a % b, x, y);
    ll t = x % mod;
    x = y % mod;
    y = ((t - a / b * y) % mod + mod) % mod;
    return r;
}