R学习之统计实验（四）--蒲丰投针（R语言编程）-----数模

##问题
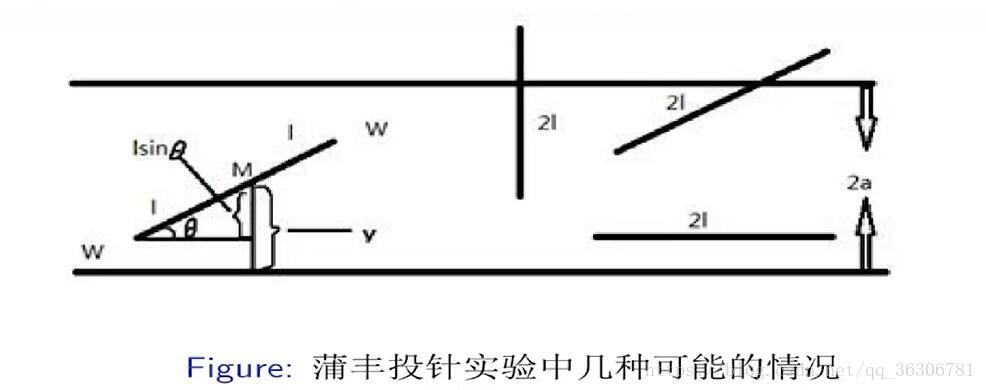
法国数学家蒲丰于1777年完成的投针实验是历史上第一个统计模拟实验，可以利用实验结果估计圆周率二.该实验可以表述为：向一簇距离为2a的平行线构成的平面中投掷一根长度为2L的针,求针与直线相交的概率 . 这里假设L< a．实验图形如下：


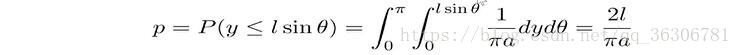
##直接R模拟（大数定律）
注意括号各种英文输入，R语言编写时候看不出明显区别

buffon<-function(n,a,L){
  m<-0
  for (i in 1:n) {
    x<-runif(1)*a
    theta<-runif(1)*pi
    if(L*sin(theta)>=x){m=m+1}
  }
  #估算概率
  p<-m/n
  #估算pi
  pie<-2*L/(a*p)
  result<-c('估计概率'=p,'pi估计值'=pie);result
}
buffon(10000,1,0.8)
buffon(10000,2,1.5)
buffon(10000,3,2)

##结果

> buffon<-function(n,a,L){
+   m<-0
+   for (i in 1:n) {
+     x<-runif(1)*a
+     theta<-runif(1)*pi
+     if(L*sin(theta)>=x){m=m+1}
+   }
+   #估算概率
+   p<-m/n
+   #估算pi
+   pie<-2*L/(a*p)
+   result<-c('估计概率'=p,'pi估计值'=pie);result
+ }
> buffon(10000,1,0.8)
估计概率 pi估计值 
0.522600 3.061615 
> buffon(10000,2,1.5)
估计概率 pi估计值 
0.476400 3.148615 
> buffon(10000,3,2)
估计概率 pi估计值 

#DONE！！！