通过分析 JDK 源代码研究 TreeMap 红黑树算法实现

通过分析 JDK 源代码研究 TreeMap 红黑树算法实现

了解 TreeMap 和 TreeSet 以及二者之间的关系

TreeMap实现SortedMap接口，能够把它保存的记录根据键排序，默认是按键值的升序排序，也可以指定排序的比较器，但用iterator遍历TreeMap时，得到的记录是排过序的。

如果使用排序的映射，建议使用TreeMap。

在使用TreeMap时，key必须实现Comparable接口或者在构造TreeMap传入自定义的Comparator，否则会在运行时抛出java.lang.ClassCastException类型的异常。

public class TreeSet<E> extends AbstractSet<E>
    implements NavigableSet<E>, Cloneable, java.io.Serializable
 {
    // 使用 NavigableMap 的 key 来保存 Set 集合的元素
    private transient NavigableMap<E,Object> m;
    // 使用一个 PRESENT 作为 Map 集合的所有 value。
    private static final Object PRESENT = new Object();
    // 包访问权限的构造器，以指定的 NavigableMap 对象创建 Set 集合
    TreeSet(NavigableMap<E,Object> m)
    {
        this.m = m;
    }
    public TreeSet()                                      // ①
    {
        // 以自然排序方式创建一个新的 TreeMap，
        // 根据该 TreeSet 创建一个 TreeSet，
        // 使用该 TreeMap 的 key 来保存 Set 集合的元素
        this(new TreeMap<E,Object>());
    }
    public TreeSet(Comparator<? super E> comparator)     // ②
    {
        // 以定制排序方式创建一个新的 TreeMap，
        // 根据该 TreeSet 创建一个 TreeSet，
        // 使用该 TreeMap 的 key 来保存 Set 集合的元素
        this(new TreeMap<E,Object>(comparator));
    }
    public TreeSet(Collection<? extends E> c)
    {
        // 调用①号构造器创建一个 TreeSet，底层以 TreeMap 保存集合元素
        this();
        // 向 TreeSet 中添加 Collection 集合 c 里的所有元素
        addAll(c);
    }
    public TreeSet(SortedSet<E> s)
    {
        // 调用②号构造器创建一个 TreeSet，底层以 TreeMap 保存集合元素
        this(s.comparator());
        // 向 TreeSet 中添加 SortedSet 集合 s 里的所有元素
        addAll(s);
    }
    //TreeSet 的其他方法都只是直接调用 TreeMap 的方法来提供实现
    ...
    public boolean addAll(Collection<? extends E> c)
    {
        if (m.size() == 0 && c.size() > 0 &&
            c instanceof SortedSet &&
            m instanceof TreeMap)
        {
            // 把 c 集合强制转换为 SortedSet 集合
            SortedSet<? extends E> set = (SortedSet<? extends E>) c;
            // 把 m 集合强制转换为 TreeMap 集合
            TreeMap<E,Object> map = (TreeMap<E, Object>) m;
            Comparator<? super E> cc = (Comparator<? super E>) set.comparator();
            Comparator<? super E> mc = map.comparator();
            // 如果 cc 和 mc 两个 Comparator 相等
            if (cc == mc || (cc != null && cc.equals(mc)))
            {
                // 把 Collection 中所有元素添加成 TreeMap 集合的 key
                map.addAllForTreeSet(set, PRESENT);
                return true;
            }
        }
        // 直接调用父类的 addAll() 方法来实现
        return super.addAll(c);
    }
    ...
 }

从上面代码可以看出，TreeSet的1号，2号构造器都是新建一个TreeMap作为实际存储Set元素的容器，而另外2个构造器则分别依赖于1号和2号构造器，由此可见，TreeSet底层实际使用的存储容器就是TreeMap。

与HashSet安全类似的是，TreeSet里绝大部分方法都是直接调用TreeMap的方法来实现的。

对于TreeMap而言，它采用一种被成为‘红黑树’的排序二叉树来保存Map中每个Entry

每个Entry都被当成‘红黑树’的一个节点对待。

public class TreeMapTest
 {
    public static void main(String[] args)
    {
        TreeMap<String , Double> map =
            new TreeMap<String , Double>();
        map.put("ccc" , 89.0);
        map.put("aaa" , 80.0);
        map.put("zzz" , 80.0);
        map.put("bbb" , 89.0);
        System.out.println(map);
    }
 }

当程序执行 map.put(“ccc” , 89.0); 时，系统将直接把 “ccc”-89.0 这个 Entry 放入 Map 中，这个 Entry 就是该”红黑树”的根节点。接着程序执行 map.put(“aaa” , 80.0); 时，程序会将 “aaa”-80.0 作为新节点添加到已有的红黑树中。

以后每向 TreeMap 中放入一个 key-value 对，系统都需要将该 Entry 当成一个新节点，添加成已有红黑树中，通过这种方式就可保证 TreeMap 中所有 key 总是由小到大地排列。例如我们输出上面程序，将看到如下结果（所有 key 由小到大地排列）：

{aaa=80.0, bbb=89.0, ccc=89.0, zzz=80.0}

红黑树

红黑树是一种自平衡排序二叉树，树中每个节点的值，都大于或等于在它的左子树中的所有节点的值，并且小于或者等于在它的右子树中的所有节点的值，这确保红黑树运行时可以快速地在数中查找和定位的所需节点。

对于TreeMap而言，由于它底层采用一颗“红黑树”来保存集合中的Entry，这意味这TreeMap添加元素，取出元素的性能都比HashMap低，当TreeMap添加元素时，需要通过循环找到新增Entry插入位置，因此比较耗费性能。当从TreeMap中取出元素时，需要通过循环才能找到合适的Entry，也比较耗费性能。TreeMap 中的所有 Entry 总是按 key 根据指定排序规则保持有序状态，TreeSet 中所有元素总是根据指定排序规则保持有序状态。

为了理解TreeMap的底层实现，必须先介绍排序二叉树和红黑树这2中数据结构。其中红黑树又是一种特殊的排序二叉树。

排序二叉树是一种特殊结构的二叉树，可以非常方便地对数中所有节点进行排序和检索。

排序二叉树要么是一颗空二叉树，要么是具有下列性值的二叉树

如果它的左子树不空，则左子树所有节点的值均小于它根节点的值

如果它的右子树不空，则右子树上的值均大于它的根节点的值

它的左右子树也分别为排序二叉树

图 1. 排序二叉树

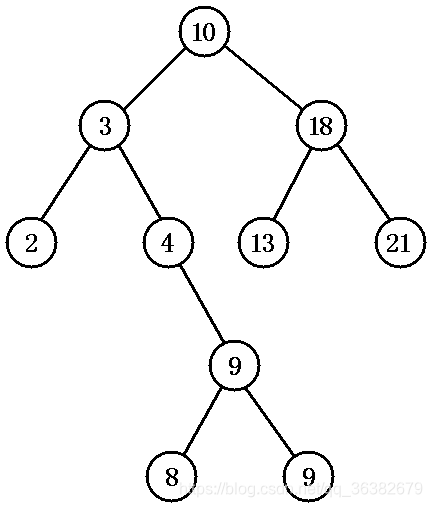
对排序二叉树，若按中序遍历就可以得到由小到大的有序序列。如图 1 所示二叉树，中序遍历得：

{2，3，4，8，9，9，10，13，15，18}

创建排序二叉树的步骤，也就是不断地向排序二叉树添加节点的过程，向排序二叉树添加节点的步骤如下

1 以根节点当前节点开始搜索

2 拿新节点的值和当前节点的值比较

3如果新节点的值更大，则以当前节点的右子节点作为新的当前节点，如果新节点的值更小，则以当前节点的左子节点作为新的当前节点。

4 重复2，3 两个步骤，知道搜索到合适的叶子节点为止。

5 将新节点添加为第4步找到的叶子节点的子节点，如果新节点更大，则添加为右子节点，否则添加为左子节点。

掌握上面理论之后，下面我们来分析 TreeMap 添加节点（TreeMap 中使用 Entry 内部类代表节点）的实现，TreeMap 集合的 put(K key, V value) 方法实现了将 Entry 放入排序二叉树中，下面是该方法的源代码

public V put(K key, V value)
 {
    // 先以 t 保存链表的 root 节点
    Entry<K,V> t = root;
    // 如果 t==null，表明是一个空链表，即该 TreeMap 里没有任何 Entry
    if (t == null)
    {
        // 将新的 key-value 创建一个 Entry，并将该 Entry 作为 root
        root = new Entry<K,V>(key, value, null);
        // 设置该 Map 集合的 size 为 1，代表包含一个 Entry
        size = 1;
        // 记录修改次数为 1
        modCount++;
        return null;
    }
    int cmp;
    Entry<K,V> parent;
    Comparator<? super K> cpr = comparator;
    // 如果比较器 cpr 不为 null，即表明采用定制排序
    if (cpr != null)
    {
        do {
            // 使用 parent 上次循环后的 t 所引用的 Entry
            parent = t;
            // 拿新插入 key 和 t 的 key 进行比较
            cmp = cpr.compare(key, t.key);
            // 如果新插入的 key 小于 t 的 key，t 等于 t 的左边节点
            if (cmp < 0)
                t = t.left;
            // 如果新插入的 key 大于 t 的 key，t 等于 t 的右边节点
            else if (cmp > 0)
                t = t.right;
            // 如果两个 key 相等，新的 value 覆盖原有的 value，
            // 并返回原有的 value
            else
                return t.setValue(value);
        } while (t != null);
    }
    else
    {
        if (key == null)
            throw new NullPointerException();
        Comparable<? super K> k = (Comparable<? super K>) key;
        do {
            // 使用 parent 上次循环后的 t 所引用的 Entry
            parent = t;
            // 拿新插入 key 和 t 的 key 进行比较
            cmp = k.compareTo(t.key);
            // 如果新插入的 key 小于 t 的 key，t 等于 t 的左边节点
            if (cmp < 0)
                t = t.left;
            // 如果新插入的 key 大于 t 的 key，t 等于 t 的右边节点
            else if (cmp > 0)
                t = t.right;
            // 如果两个 key 相等，新的 value 覆盖原有的 value，
            // 并返回原有的 value
            else
                return t.setValue(value);
        } while (t != null);
    }
    // 将新插入的节点作为 parent 节点的子节点
    Entry<K,V> e = new Entry<K,V>(key, value, parent);
    // 如果新插入 key 小于 parent 的 key，则 e 作为 parent 的左子节点
    if (cmp < 0)
        parent.left = e;
    // 如果新插入 key 小于 parent 的 key，则 e 作为 parent 的右子节点
    else
        parent.right = e;
    // 修复红黑树
    fixAfterInsertion(e);                               // ①
    size++;
    modCount++;
    return null;
 }

上面程序中粗体字代码就是实现”排序二叉树”的关键算法，每当程序希望添加新节点时：系统总是从树的根节点开始比较 —— 即将根节点当成当前节点，如果新增节点大于当前节点、并且当前节点的右子节点存在，则以右子节点作为当前节点；如果新增节点小于当前节点、并且当前节点的左子节点存在，则以左子节点作为当前节点；如果新增节点等于当前节点，则用新增节点覆盖当前节点，并结束循环 —— 直到找到某个节点的左、右子节点不存在，将新节点添加该节点的子节点 —— 如果新节点比该节点大，则添加为右子节点；如果新节点比该节点小，则添加为左子节点。

TreeMap 的删除节点

当程序从排序二叉树中删除一个节点之后，为了让它依然保持为排序二叉树，程序必须对该排序二叉树进行维护。维护可分为如下几种情况：

（1）被删除的节点是叶子节点，则只需将它从其父节点中删除即可。

（2）被删除节点 p 只有左子树，将 p 的左子树 pL 添加成 p 的父节点的左子树即可；被删除节点 p 只有右子树，将 p 的右子树 pR 添加成 p 的父节点的右子树即可。

（3）若被删除节点 p 的左、右子树均非空，有两种做法：

• 将 pL 设为 p 的父节点 q 的左或右子节点（取决于 p 是其父节点 q 的左、右子节点），将 pR 设为 p 节点的中序前趋节点 s 的右子节点（s 是 pL 最右下的节点，也就是 pL 子树中最大的节点）。
• 以 p 节点的中序前趋或后继替代 p 所指节点，然后再从原排序二叉树中删去中序前趋或后继节点即可。（也就是用大于 p 的最小节点或小于 p 的最大节点代替 p 节点即可）。

被删除节点只有左子树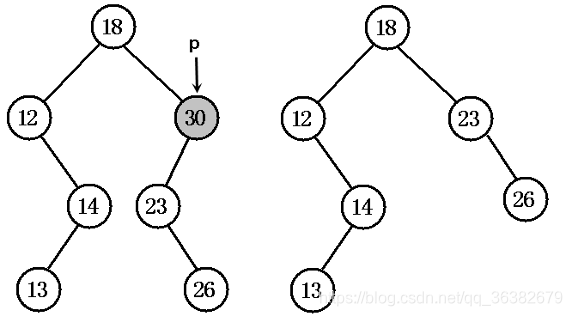

被删除节点只有右子树

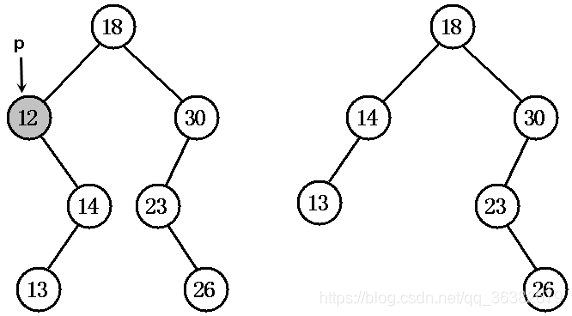
被删除节点既有左子树，又有右子树

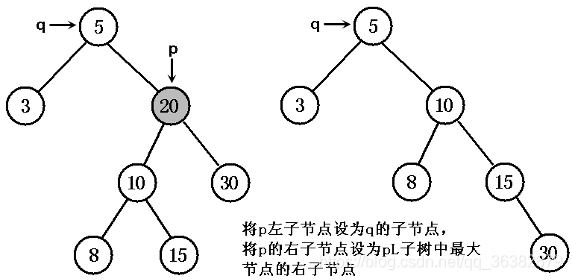
被删除节点既有左子树，又有右子树

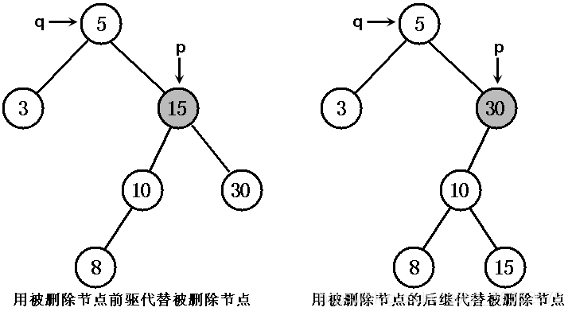
TreeMap 删除节点的方法由如下方法实现：

private void deleteEntry(Entry<K,V> p)
 {
    modCount++;
    size--;
    // 如果被删除节点的左子树、右子树都不为空
    if (p.left != null && p.right != null)
    {
        // 用 p 节点的中序后继节点代替 p 节点
        Entry<K,V> s = successor (p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    }
    // 如果 p 节点的左节点存在，replacement 代表左节点；否则代表右节点。
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);
    if (replacement != null)
    {
        replacement.parent = p.parent;
        // 如果 p 没有父节点，则 replacemment 变成父节点
        if (p.parent == null)
            root = replacement;
        // 如果 p 节点是其父节点的左子节点
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        // 如果 p 节点是其父节点的右子节点
        else
            p.parent.right = replacement;
        p.left = p.right = p.parent = null;
        // 修复红黑树
        if (p.color == BLACK)
            fixAfterDeletion(replacement);       // ①
    }
    // 如果 p 节点没有父节点
    else if (p.parent == null)
    {
        root = null;
    }
    else
    {
        if (p.color == BLACK)
            // 修复红黑树
            fixAfterDeletion(p);                 // ②
        if (p.parent != null)
        {
            // 如果 p 是其父节点的左子节点
            if (p == p.parent.left)
                p.parent.left = null;
            // 如果 p 是其父节点的右子节点
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
 }
    // ②
        if (p.parent != null)
        {
            // 如果 p 是其父节点的左子节点
            if (p == p.parent.left)
                p.parent.left = null;
            // 如果 p 是其父节点的右子节点
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
 }