Non-Local Recurrent Network for Image Restoration 论文笔记

论文地址：http://papers.nips.cc/paper/7439-non-local-recurrent-network-for-image-restoration.pdf

摘要

目前许多经典的方法已经证明了自然图片的自我相似度(non-local self-similarity)可以作为图像重建任务中一个有效的先验知识。然而让神经网络合理的利用这一图片固有属性仍旧是一个挑战性任务。这篇论文中作者提出了非局部循环网络(non-local recurrent network,NLRN)，完成图像重建任务，主要贡献如下：

• 将non-local 操作加入了神经网络中进行端到端的训练去捕捉一个特征与其邻近的特征的相关性
• 使用循环神经网络框架(RNN)较好的提高了参数的利用率，且较好的提高了模型的鲁棒性
• 证明了计算特征相似度时，限制相邻特征的范围对图像修复 任务十分重要

方法概述

non-local 操作

整体来说，non-local操作需要输入一个N*M的图片特征X，然后重新计算得到新的特征向量$Z\in R^{N\times k}$。N指代图片像素个数，m,k指代的是通道个数。公式描述如下：

其中$\Phi (X)\in R^{(}N\times N)$是non-local关联矩阵，$G(X)\in R^{N\times k}$为多通道非局部转换操作。 d i a g { δ ( X ) } diag\{\delta(X)\} diag{δ(X)}为对角矩阵，其规范化输出大小作用，具体实现如下：

其中$\Phi (X{)}_i^j$代表了局部向量$X_i$和$X_j$的关系。
已有的non-local操作均为直接在整个图的范围计算每个局部特征之间的相关性，然后进行特征重组，但是这种方法由于其参数是固定的因此无法得到问题的最优解。为此作者设计了全新的Non-local 模块，并将其加入神经网络中，希望通过模型训练来得到图像重建问题的最优解。具体操作如下图所示：

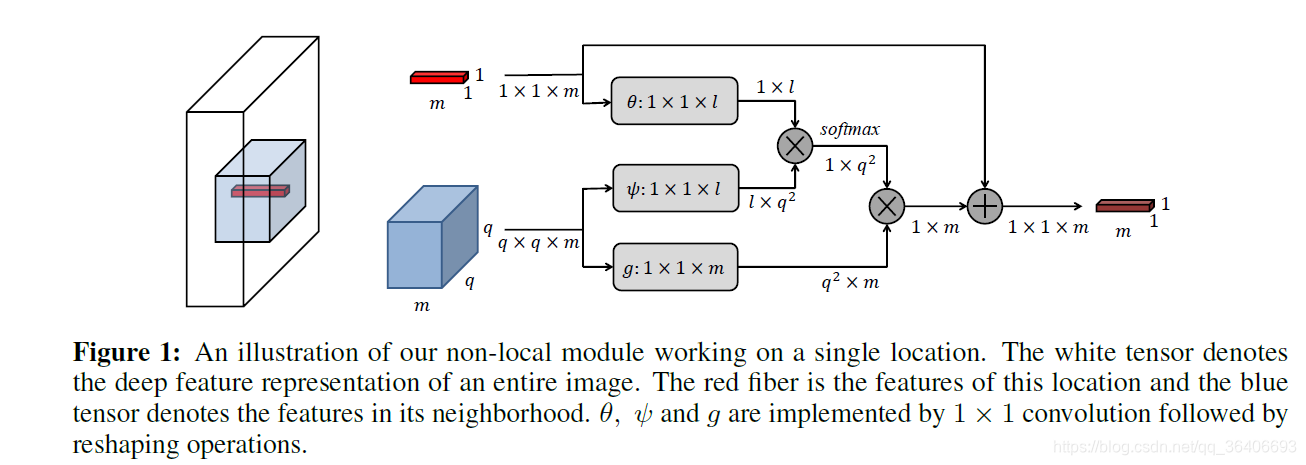
首先先对待重建的特征m进行卷积，然后用两个不同的卷积核对m的q*q大小的邻居进行卷积操作，将得到的$\psi$与$\theta$相乘得到相似度矩阵，然后降相似度矩阵与卷积提取到的特征g相乘进行重建，重建结果与原始的m相加得到最终的输出m。作者提出的non-local操作因为加入到了神经网络中，并引入了可学习的参数进行调节，能够更精准的根据已知区域推断出缺失区域的像素信息，且模型拥有更高的鲁棒性。因在non-local操作中使用的卷积核的大小均为1，模型的参数量也依旧很小。此外，作者经验性的通过实验证明了不需要从全图范围计算相似度，选取一个最合适的邻居大小q，能够得到最好的结果。

Non-Local Recurrent Network

除了改进的non-local操作，作者降non-local操作与循环神经网络结合到了一起，以便于能够提高模型参数的利用效率以及提高模型的鲁棒性，具体的操作如下图所示：

作者采用了最普通的循环神经网络单元，包括输入状态，输出状态，循环状态以及状态转换方程。经过时间t个循环以后得到模型的最终结果。图中$s^t$代指t时刻时的结果,$s_{feat}^0$ 代表输入的特征图。$s_{corr}^t$代表关联矩阵。从图中可以看出，每一个时刻计算关联矩阵的时候，都会加上上一个时刻的softmax之前的关联矩阵，以此来提高关联矩阵的准确性，进一步提高了模型的鲁棒性。

实验结果

因为较为灵活的non-local，模块该该方法在图片降噪以及超分辨任务上都取得了较好的结果，具体如下：

总结

虽然论文里并没有提出了某种具体的图像修复框架，但是其新颖的non-local操作，对于我们对如何合理的引导模型将已知区域的信息传播到未知区域有了更深的认知。我们以后无论是在图像修复任务或是超分辨任务上，均可以将这种思想进行变种，来进一步提高我们自己模型的效果