动态规划--数塔

数塔是动态规划的一道经典题
认识数塔前，先认识一下动态规划，动态规划不是一种特定的算法，而是一种具有较强的技巧性的手段，或者说是思想，但所有动态规划的题离不开两个核心：
1.状态
2.状态转移方程
当我们抓住这两个核心，我们的问题就能解决一大半！
—————————————————————————————————————
题目：

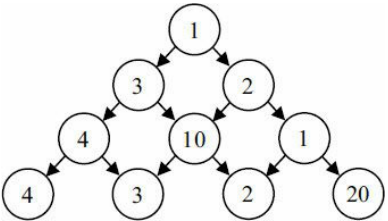
图片上便是一个数塔，现在要解决的问题是，从数塔顶层到底层，沿途将权重（即数值）相加和最大是多少？

分析：
首先再回想一遍动态规划的两个核心。
状态分析：我们会发现，当在每个节点都会做一个选择，（例如：在1时，是选择左还是选择右）
而选择了左或者右的时候又继续会有选择，我们此时马上就会想到递归（见a）
状态转移方程分析：题目要求最大的走法，所以我们可以初步得出一个方程雏形
a[选择后的结果]=b[节点]+max(a[左],a[右])
现在就需要一点点技巧性了，如何将方程雏形改成真正的状态转移方程
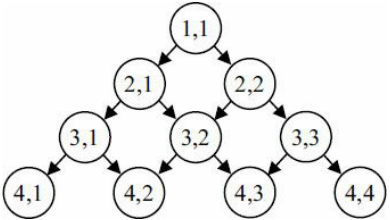
此处我们给出一个二维数组的处理办法，如图所示：

即可得出状态转移方程：
a[i,j]=b[i,j]+max(a[i+1,j],a[i+1,j+1])
理解了题目的状态，得出状态转移方程后，便要考虑计算的问题了
- a
-递归计算
！！注意边界处理，递归没有什么要讲的，直入代码

int dp(int i,int j)
{
	if(i<=n)
		return b[i,j]+max(dp(i+1,j),dp(i+1,j+1))
	if(i>n)
		return 0;
}