基于自适应光学系统高分辨率成像系统技术研究——动画演示原理

摘要

本博文主要聚焦于基于自适应光学系统的高分辨率成像技术研究，成功实现了对分辨率板的高分辨率成像模拟。文章首先深入介绍了柯尔莫哥洛夫湍流模拟(Kolmogorov)，由于湍流畸变的影响，导致获取的图像质量退化。随后，通过应用自适应光学闭环畸变校正技术(即基于波前传感的梯度下降法)，成像质量得到了显著提升。此外，博文还以动画示意图的形式，生动展示了整个自适应光学系统高分辨率成像的过程，使得对有波前传感的梯度下降算法的理解更为直观。同时，文章还对无波前传感的随机并行梯度下降算法进行了简要介绍。

一、柯尔莫哥洛夫湍流模拟(Kolmogorov)

大气湍流引起的波前畸变，可以展开为各阶泽尼克多项式的线性叠加，且各阶泽尼克多项式系数发生随机变化。泽尼克多项式的特性，是将径向特征和角向特征分部描述，在极坐标系中，能够非常方便地表示为极角函数和矢径多项式的乘积。泽尼克多项式定义为

式中的j为泽尼克多项式的阶数，参数m和n分别代表角向频率和径向次数。类似于傅里叶频谱分析m和n越大，所代表的频率就越高。m和n按照一定的排列顺序是j的函数。j、m和n是整数，且满足条件

当用泽尼克多项式描述大气湍流引起的波前畸变时，各阶泽尼克多项式模式之间的统计相关性，和大气湍流波前畸变的统计特性有着内在联系。波前畸变的泽尼克多项式系数，可以被认为是零平均值的高斯随机变量。利用傅里叶变换中的瑞利定理，Kolmogorov大气湍流中各阶泽尼克多项式系数的协方差，可以由相位起伏的Wiener功率谱给出

其中， 和 是第 j 和第j’阶泽尼克多项式的系数。n, m 是第 j 阶泽尼克多项式的参数，n’ 和 m’ 是第j’阶泽尼克多项式的参数。 是关于 m 和 m’ 的 Kronecker 函数，如果 m = m’ = 0，则 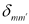= 1；如果m=m’≠ 0，且 j 和j’有相同的奇偶性，则 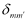= 1；其他情况下 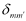= 0。D 为光瞳的直径，r0 为 Fried 常数， 是 Gamma 函数。上式构成一个对称的泽尼克模式统计相关矩阵，其对角线元素正比于 Kolmogorov端流下各阶泽尼克模式的方差[1]。

本文用泽尼克多项式模拟了符合Kolmogorov谱的湍流相位屏，采用了前37阶泽尼克多项式基模拟的大气湍流相位屏畸变波前分布如下图所示：

图1 模拟的大气湍流相位屏畸变波前

二、自适应光学系统波前校正高分辨率成像实验

2.1 有波前传感的梯度下降算法

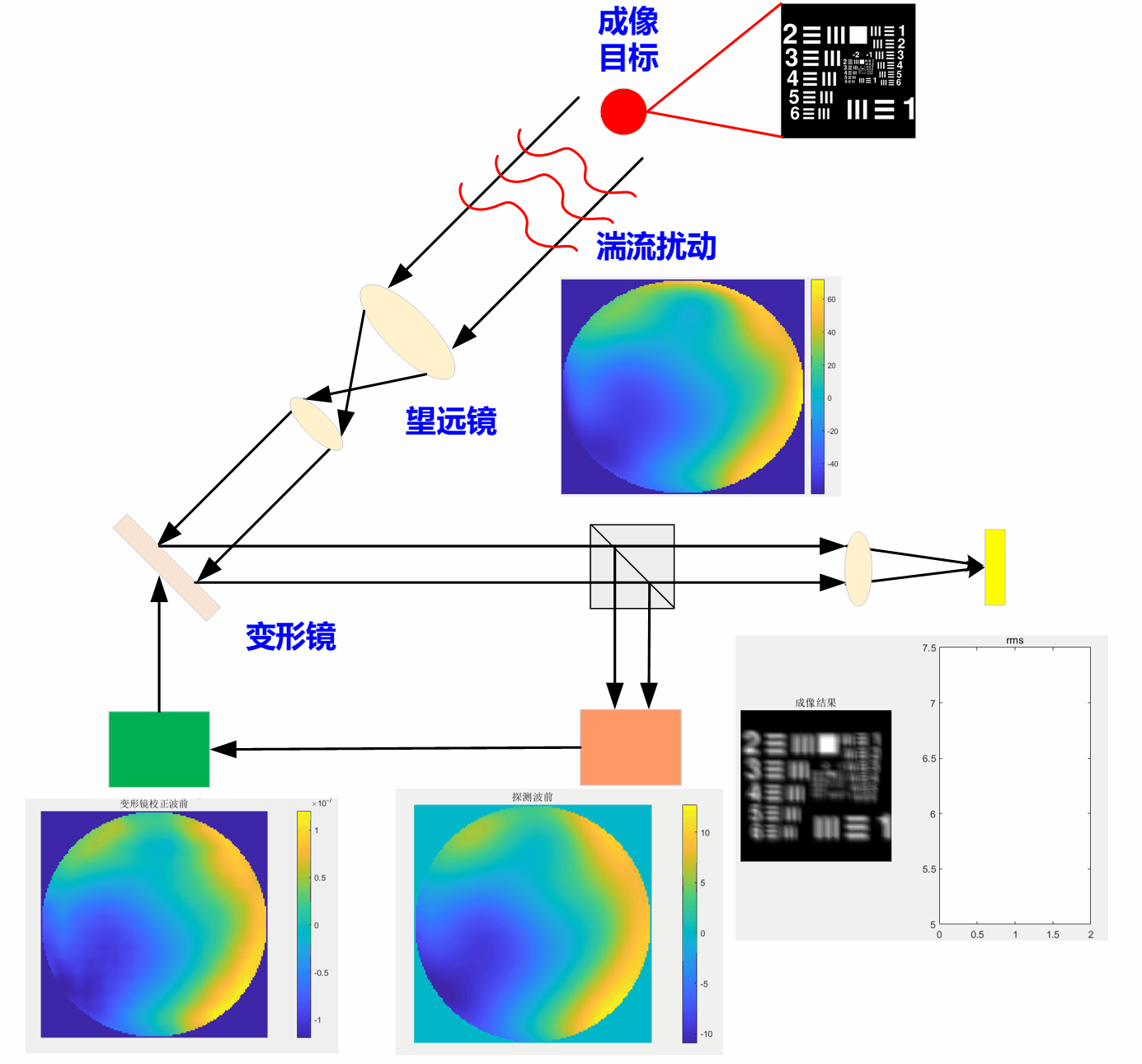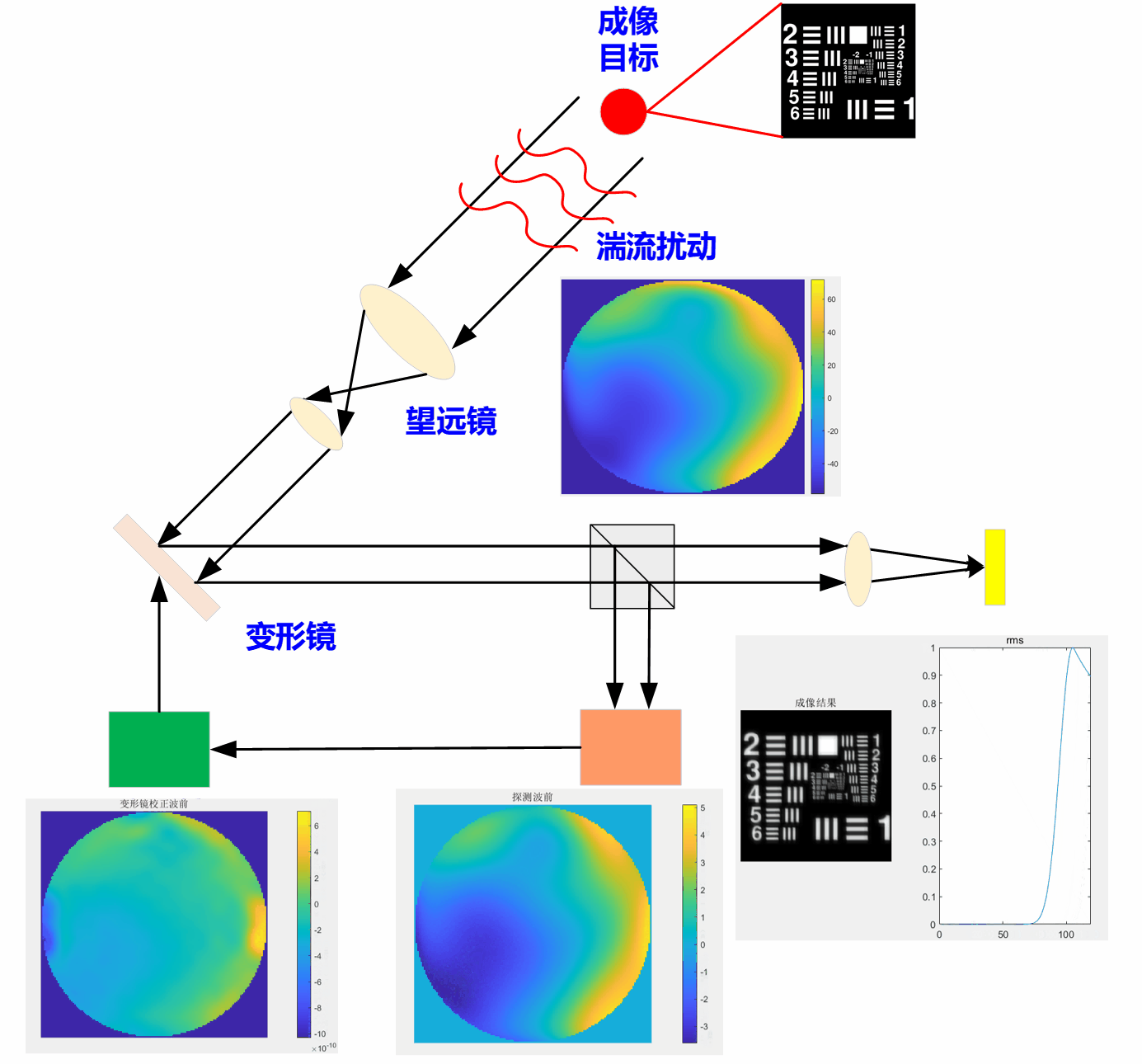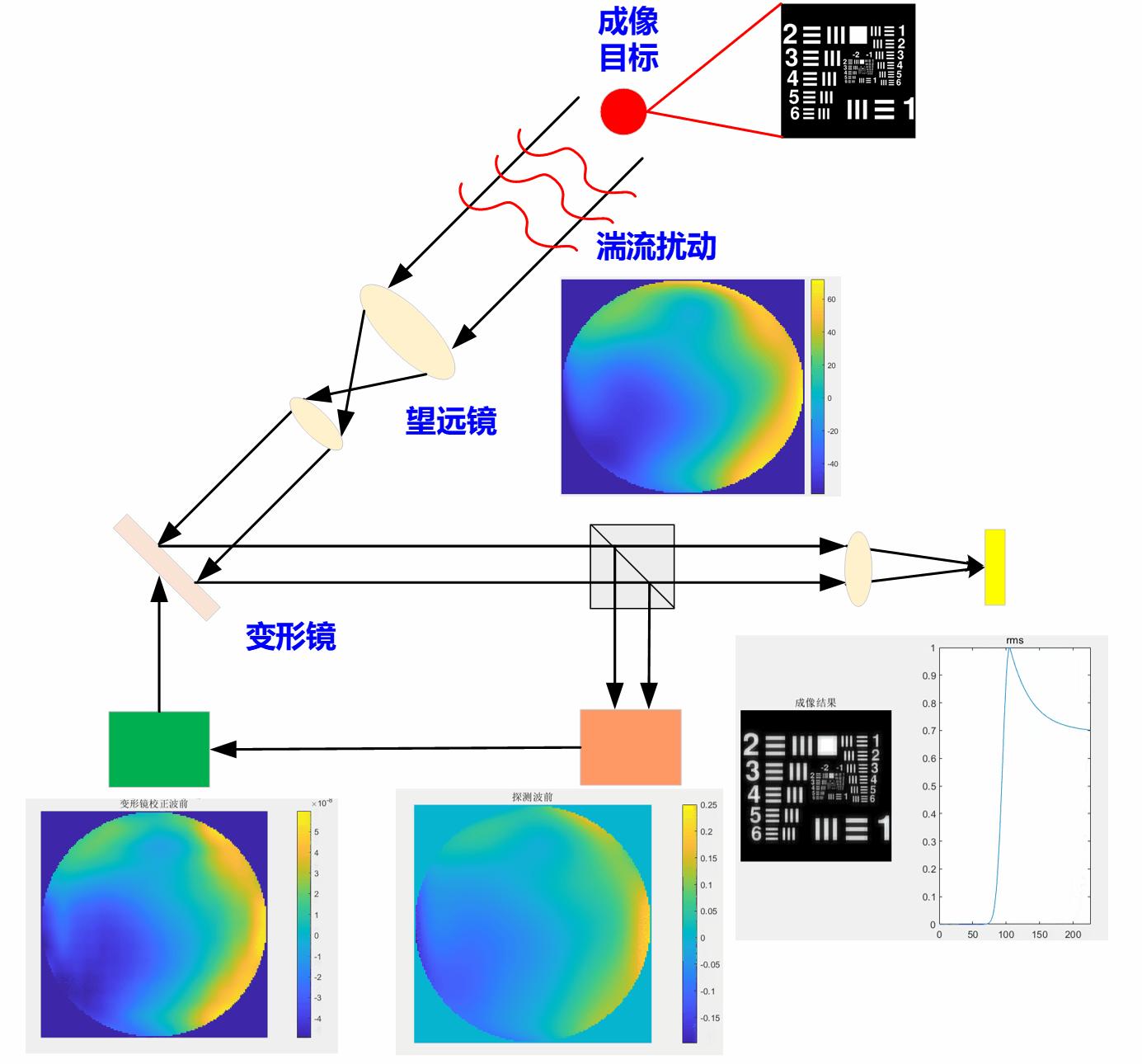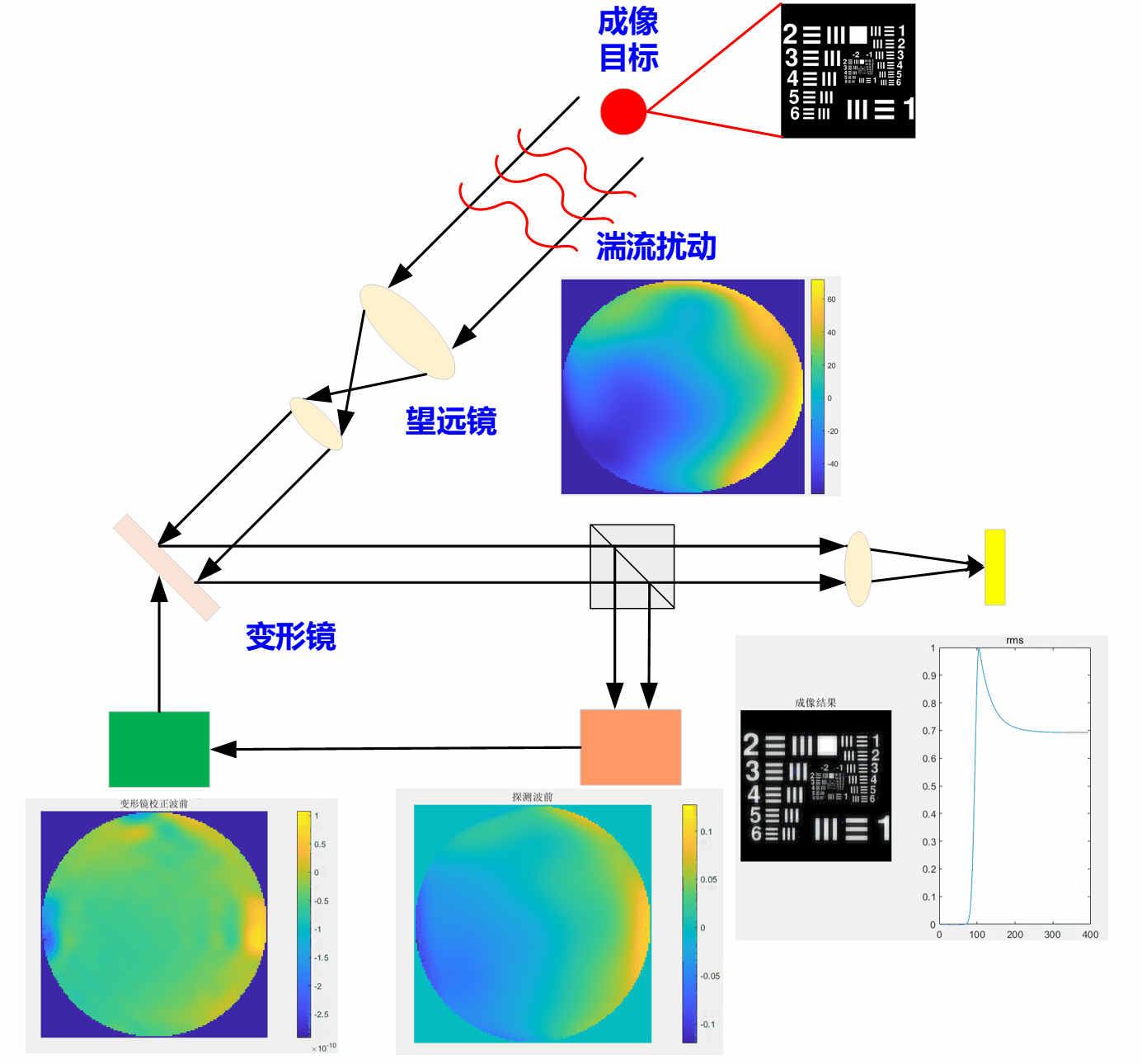
自适应光学系统主要可分为无波前测量型和有波前测量型。图2为有波前探测型自适应光学系统原理图。其中，波前传感器实时测量波前误差，并把测量到的波前误差传送给波前控制器；波前控制器接收来自波前传感器的畸变光束信息，并通过一定算法计算、获取波前校正器的控制电压；波前校正器接收来自波前控制器的控制电压，校正波前畸变，提升成像质量。

图2 自适应光学系统原理图

当从待探测物体发出的近似平面波穿过湍流扰动场后，波前会受到大气湍流的影响而发生畸变，导致成像质量下降。为了纠正这种畸变，自适应光学系统被引入，其中波前校正器(变形镜)和波前探测器(哈特曼波前传感器)起到了关键作用。自适应光学波前校正的理论依据是相位共轭（Phase Conjugation），首先，哈特曼波前传感器实时探测并记录波前畸变的斜率信息。接下来，自适应光学系统的波前控制器接收哈特曼波前传感器提供的斜率信息，并计算出相应的共轭相位。共轭相位是指与当前哈特曼波前传感器探测到的波前畸变相位相反的相位分布，通过加载共轭相位到变形镜上，可以实现对波前畸变的实时校正。变形镜是一个可变形的光学元件，能够根据波前控制器的指令(即电压值)调整其表面形状。通过加载共轭相位到变形镜上，可以使其产生与波前畸变相反的相位变化，从而纠正波前畸变。这样，当近似平面波再次经过变形镜时，其波前畸变会被有效地纠正，使得成像质量得到显著提升。

图3给出了自适应光学波前闭环校正高分辨成像系统详细流程，首先在Matlab中模拟出一个符合Kolmogorov谱的湍流相位屏(图3中的步骤①)，此时CCD相机探测到物体的像(图3中的步骤②)是模糊的，这是由于受到了湍流畸变的影响，降低了成像质量。接着由哈特曼波前传感器探测当前系统的畸变像差，图3中的步骤③，并将探测到的波前斜率(即电压值)传递给变形镜。变形镜获取哈特曼波前传感器探测电压值的传递方式有多种，比如固定增益，自适应增益等方式。变形镜通过哈特曼波前传感器探测的电压值驱动变形镜实现波前调控，如图3中的步骤④，此时，变形镜调制的波前是哈特曼波前探测波前的共轭(简单来说，波前互为共轭就是指一正一负的波前，这样当变形镜波前完全是畸变波前的相反相位时，即可消除畸变)。当变形镜实现一次波前补偿时，CCD相机成像质量将发生改变，如图3中的步骤⑤。整个过程实现了1次迭代的闭环校正。

图3 自适应光学波前闭环校正高分辨成像系统

然而，由于无法通过一次迭代就实现完美的畸变波前校正，达到高分辨成像效果。而需要哈特曼波前传感器不断去探测补偿后系统剩余的畸变波前，并且由变形镜来逐步校正这些系统剩余畸变，直到达到CCD相机获得高分辨的成像目标。图4给出了第300次迭代的闭环畸变校正后的成像结果，结果表明，经过不断迭代校正后，已经能够实现高分辨成像，此时成像质量(RMS值，可从动图中观察)已经趋于稳定。且图4中还可看出，经过300次的迭代校正，此时，系统中存在的畸变波前(图4步骤③、步骤④)相比与步骤①，已经小很多了。

闭环校正的思想，实质上可视为一种结合了哈特曼波前传感的梯度下降校正策略(或者称之为传统梯度下降法)。在此策略中，哈特曼波前传感器发挥着关键作用，它负责捕捉波前斜率获得电压值以 指导梯度的调整。然而，一个值得深思的问题是，如果系统中去除了哈特曼波前传感器，我们是否还能实现有效的波前校正呢？为了解决这一问题，无波前传感的随机并行梯度下降算法（Stochastic Parallel Gradient Descent，SPGD）应运而生，其原理将在下一节中详细阐述。

图4 自适应光学波前闭环校正高分辨成像系统-第300次迭代校正时

基于自适应光学波前闭环校正高分辨成像结果如下动图所演示：

其中，闭环校正后CCD实时成像结果动图如下：动图中可以看到，随着迭代次数的增加，成像质量逐渐提升(rms值越小表示成像质量越好)，最后将趋于稳定。意味着系统中的畸变几乎已被校正。

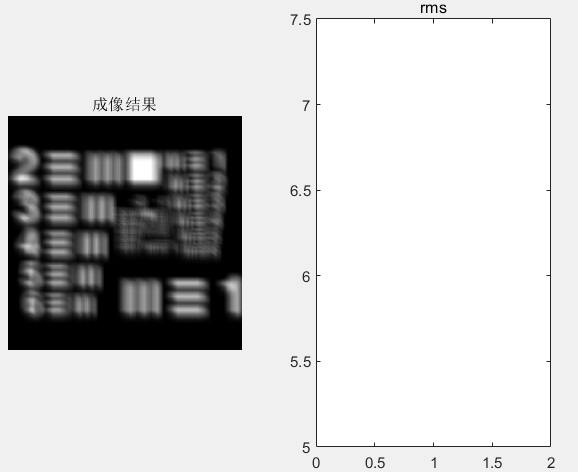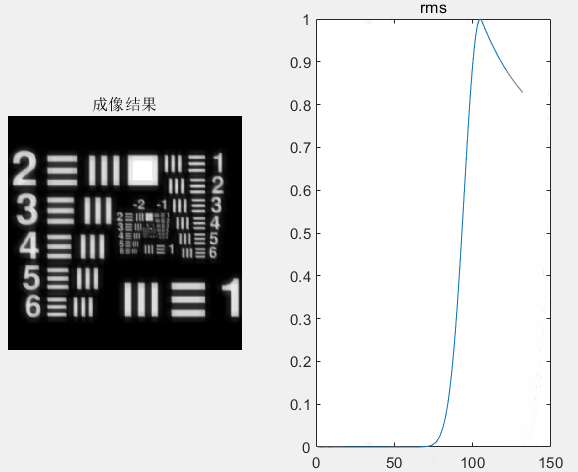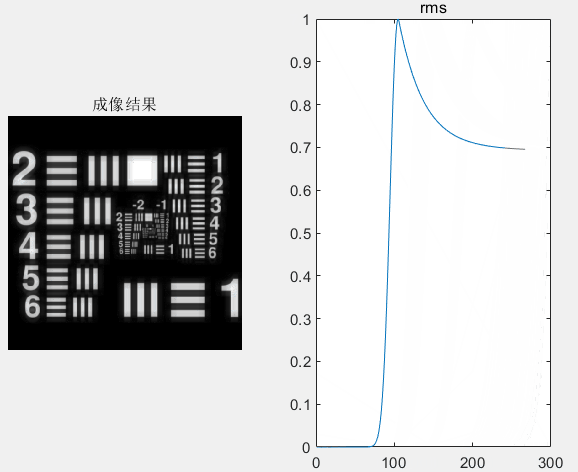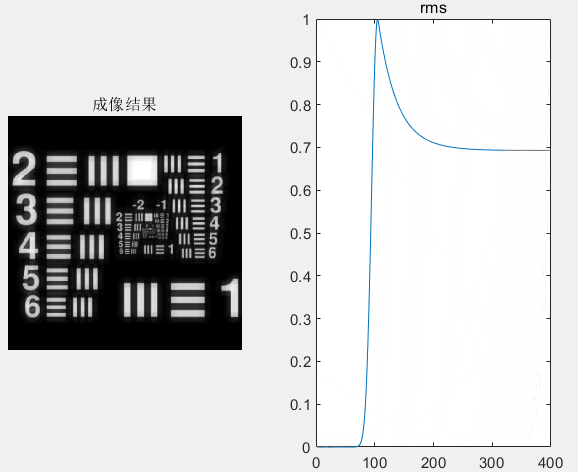
每一次迭代校正中哈特曼波前传感器探测到波前畸变动图如下：

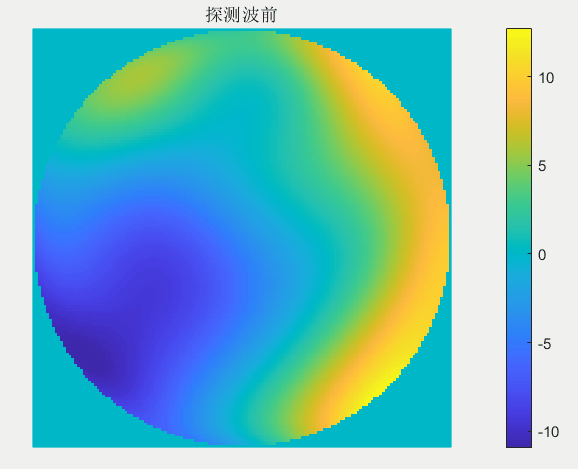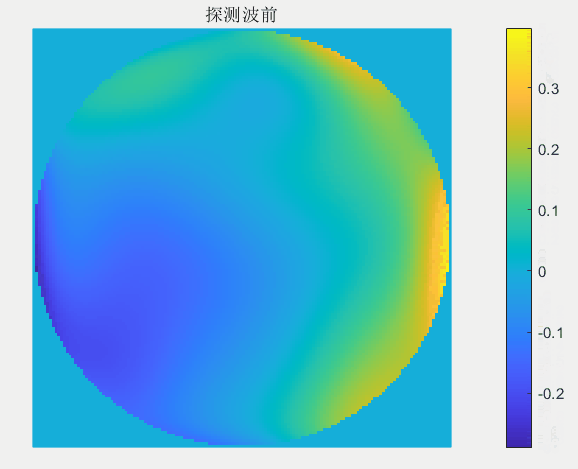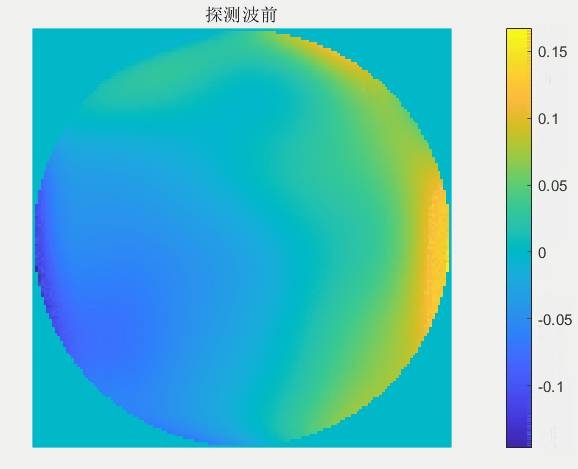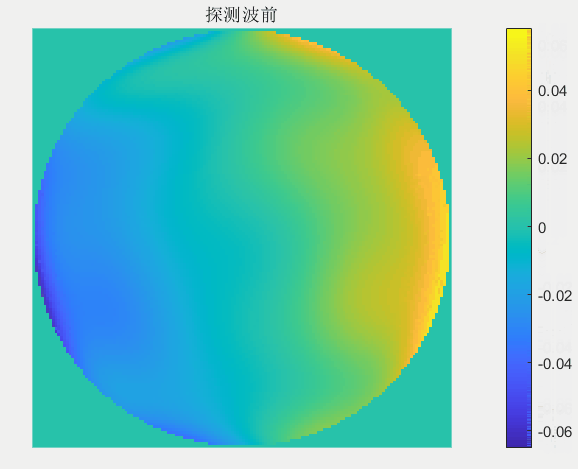
每一次迭代校正中变形镜调制的波前动图如下：

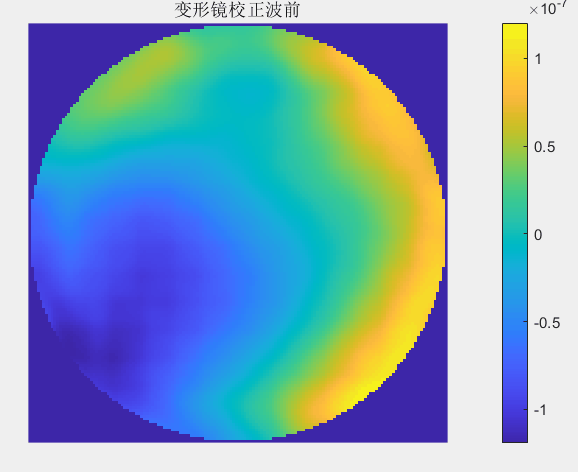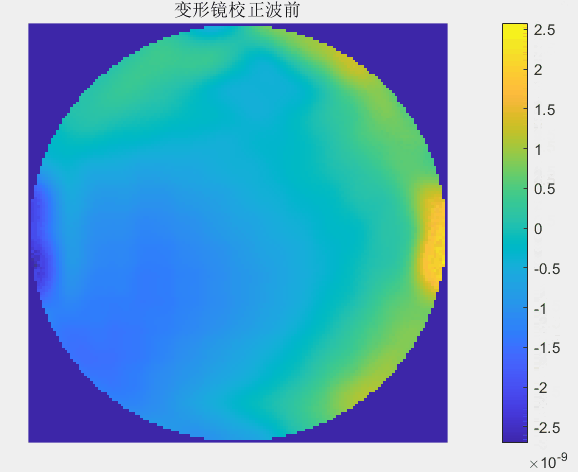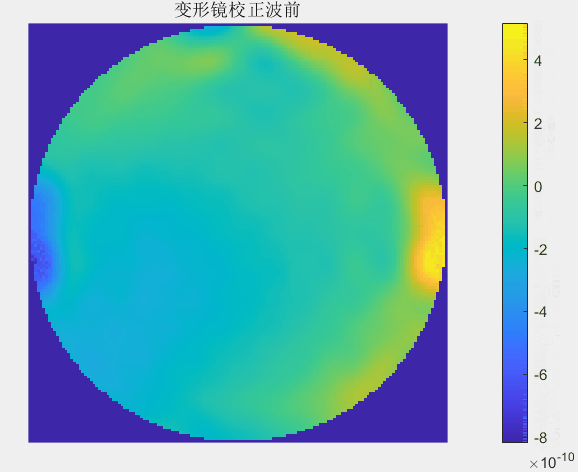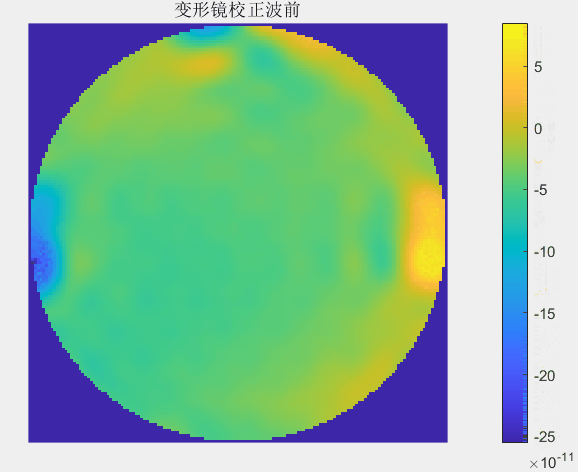
2.2 无波前传感的随机并行梯度下降算法SPGD

2.1节中描述了有波前传感的梯度下降算法，其基本原理是哈特曼波前传感器在这个过程中用于获取电压值，进而指导梯度的调整，以实现波前校正。至于无波前传感的随机并行梯度下降算法（Stochastic Parallel Gradient Descent，SPGD），其基本原理是在没有波前传感器的情况下，通过随机并行的方式调整参数，并观察系统响应来优化性能。这种方法不需要依赖波前传感器提供的实时反馈信息，而是通过试错的方式逐步逼近最优解。

图5 SPGD算法流程图

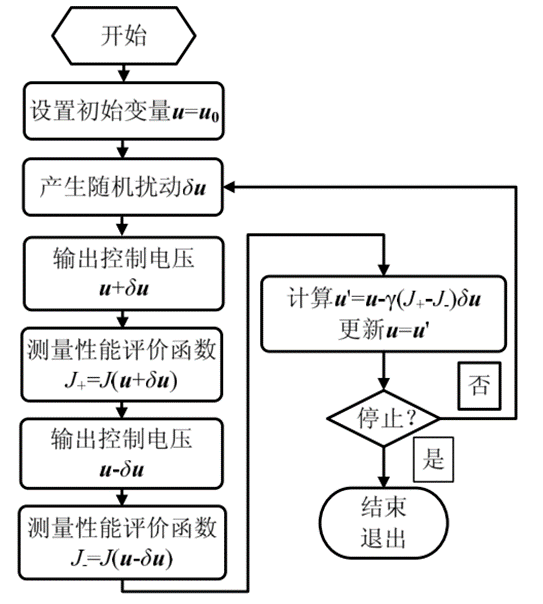
设随机扰动的统计特性服从 Bernoulli分布。SPGD 算法的具体实现步骤如下[2]：
（1）设置当前电压 u=u0 ，其中 u0 为初始电压，对于动态湍流校正实验，初始电压一般为系统静态像差补偿后波前校正器所施加的电压，当初始电压未知时，可以设定为 0；
（2）产生服从伯努利分布的随机扰动δu；
（3）将δu叠加在控制电压 u上后计算扰动后的性能评价函数J+=J(u+δu)

（4）将第（2）步产生的随机变量δu反号后，再叠加在控制电压 u上计算负向扰动后的性能评价函数J-=J(u-δu) ，然后计算性能评价函数的改变量δJ=(J±J-)/2

（5）计算出下一步迭代的控制电压u’=u+γδJδu后，更新控制电压，令 u=u’
（6）转入第（2）步继续进行迭代直到满足迭代终止条件；
对于动态波前畸变的校正， SPGD 算法一直保持迭代运行，直至迭代终止，系统退出；对于静态波前畸变的校正迭代终止条件为δJ小于某个阈值且 J大于或者小于（大于或者小于取决于性能评价函数极大化或者极小化）某个阈值，或者迭代步数达到设定值。

三、其他应用

3.1 自适应光学中人眼像差测量及校正

由于人眼光学系统不是理想的光学系统，从眼底视网膜上反射的光束波前会发生畸变，畸变波前在到达像面时无法形成清晰像，为此可以通过波前传感器、波前处理器（ PC）和波前校正器三者协调工作消除成像系统中的像差。从眼底出射的畸变波前经由 L1 和 L2 组成的孔径匹配系统后在微机械薄膜变形上反射，再进入由 L3 和 L4 组成的孔径匹配系统，最后进入 H-S 波前传感器，波前传感器测出的畸变像差由波前处理器进一步处理后得到变形镜的控制信号，经过数模转换、高压放大后得到控制电压，施加至变形镜，使变形镜镜面产生相应变形，即镜面形状与畸变波前形状为相位共轭，从而补偿畸变波前。 H-S 波前传感器继续测量变形镜校正之后的残余像差，计算新的控制信号（电压），变形镜在新的控制电压下继续校正残余像差，如此迭代循环，直至测量的残余像差满足成像条件（即由分光镜 BS 反射的光束波前为理想波： RMS 值小于 0.07λ）时为止。根据光线可逆原理，当来自眼底的光束被校正为理想波前时，在像平面上便会形成清晰的眼底像。由于变形镜校正后的残差结果作为下一次校正对象，因此上述过程属于波前像差闭环校正（补偿）模式。为满足自适应光学实时性要求，在闭环校正过程中应尽量减小波前像差测量时间和控制信号计算时间。

图6 自适应光学系统波前闭环补偿原理示意图[3]

3.2 薄膜空间望远镜高分辨成像

1953年，美国科学家巴布科克首次提出了自适应光学的概念，限于当时的科学技术水平，自适应光学仅是美好的憧憬。1972年，世界上首套基于干涉仪和变形镜的自适应光学系统实现了大气湍流的补偿。1982年，美国将自适应光学系统用于夏威夷毛伊岛上的高分辨监测空间目标望远镜。随后自适应光学技术广泛应用于地基天文望远镜、眼底成像、共焦显微镜成像、光学相干层析成像OCT等成像领域，成为了高分辨成像不可缺少的技术。

图7 自适应光学高分辨成像[4]

四、参考文献

[1] 习锋杰. 光栅型曲率传感器的设计与应用研究 [D]; 国防科学技术大学, 2010.
[2] 亓波. 量子通信光学地面站ATP关键技术研究 [D]; 中国科学院研究生院（光电技术研究所）, 2014.
[3] 钮赛赛. 基于自适应光学高分辨率微型成像系统关键技术研究 [D], 2012.
[4] 文良华. 薄膜成像中的自适应光学技术研究 [D]; 中国科学院大学(中国科学院光电技术研究所), 2019.

五、实验指导与程序获取

---

⭐️◎⭐️◎⭐️◎⭐️ · · · **博 主 简 介** · · · ⭐️◎⭐️◎⭐️◎⭐️ ♪

▁▂▃▅▆▇ 博士研究生 ，研究方向主要涉及定量相位成像领域，具体包括干涉相位成像技术(如**全息干涉☑**、散斑干涉☑等)、非干涉法相位成像技术(如波前传感技术☑，相位恢复技术☑)、条纹投影轮廓术(相位测量偏折术)、此外，还对各种相位解包裹算法☑，相干噪声去除算法☑等开展过深入的研究。

程序获取、程序开发、实验指导，软硬系统开发，科研服务，请私信博主，联系方式如下。

---