文章目录
题目要求及材料下载链接:Coursera下载地址
没用的信息略过,有用的翻译一下。

本练习需要的文件我已经打钩了。
- ex1.m - Octave/MATLAB脚本,引导你完成练习
- ex1 multi.m - 练习后面部分的Octave/MATLAB脚本
- ex1data1.txt - 单变量线性回归数据集
- ex1data2.txt - 多变量线性回归数据集
- submit.m - 交作业的脚本
- * warmUpExercise.m - Octave/MATLAB中的简单示例函数
- * plotData.m - 显示数据集的函数
- * computeCost.m - 计算线性回归代价函数的函数
- * gradientDescent.m - 梯度下降的函数
- + computeCostMulti.m - 多变量线性回归代价函数
- + gradientDescentMulti.m - 多变量线性回归梯度下降
- + featureNormalize.m - 标准化特征量
- + normalEqn.m - 计算正规方程
* 表示你需要完成的文件
+ 选做

在本练习中,使用脚本ex1.m和ex1 multi.m。这两个文件已经写好了,你不要改了。你只需要按照本作业中的说明修带星号的文件即可。对于这个练习,只需要完成练习单变量实现线性回归即可,多变量的线性回归量力而行。
1 简单函数


ex1.m的第一部分给你练习Octave/MATLAB语法和作业提交过程。在文件warmUpExercise.m中,你会发现一个Octave/MATLAB函数的轮廓。通过填写以下代码对其进行修改,以返回一个5 x 5的单位矩阵:
A = eye(5);
完成后,运行ex1.m(确保你的文件放在path中或者在当前目录中,在Octave/MATLAB提示符下键入“ex1”),正确的话应该嫩看到一个5×5的单位矩阵。
运行完刚才这个warmUpExercise函数之后ex1.m会暂停,直到你按下任意键继续执行,键入ctrl+c可以停止运行。

1.1 提交解决方案

完成练习的一部分后,在Octave/MATLAB命令行键入submit交作业进行评分。提交脚本将提示输入登录电子邮件和提交令牌,并询问想要提交哪些文件。你可以从分配的网页中获取提交令牌。多次提交取最高分。
这个交作业是对于Coursera网站说的。Linear Regression | Coursera
网站会给出你的提交令牌。

按步骤来,弄完之后会直接显示分数的。

2 单变量线性回归

在本练习的这一部分,你需要用单变量线性回归来预测快餐车的利润。现在假设你是一家餐厅的CEO,正在考虑在不同的城市开设一家新的分店。该连锁店已经在不同的城市有快餐车了,并且你还知道这些城市的利润和人口数据。


你需要用这些数据来预测接下来在哪里开店。文件ex1 data1.txt包含我们的线性回归问题的数据集。第一栏是一个城市的人口,第二栏是那个城市的餐车利润,利润的负值表示亏损。ex1.m脚本已经写好,可以直接加载这些数据。
2.1 绘制数据图

在开始任何任务之前,通常可以通过可视化来理解数据。对于本实验的数据集,您可以使用散点图来可视化数据,因为它只有两个属性要绘制(利润和人口)。(现实生活中你会遇到的很多其他问题都是多维度的,无法在二维图上画出来。)

在ex1.m中,数据被载入到变量X和y中,框框里的代码就是说怎么实现的这一步,这段代码写在ex1.m里边,你不需要对其进行修改。

接下来,脚本调用plotData来创建数据的散点图。你的工作是完成plotData.m然后画出图形;修改文件并填写以下代码:(就是你直接把下边那段代码写进文件plotData里就行了。)
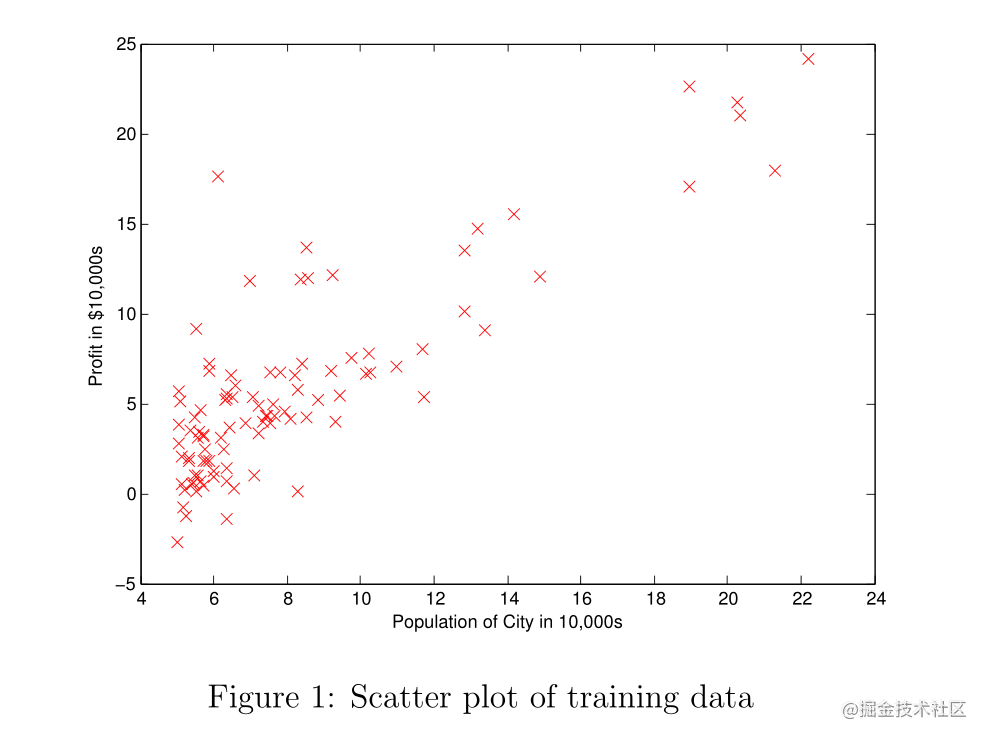
现在,继续运行ex1.m时,我们的最终结果应该如图1所示,带有相同的红色“x”标记和轴标签。
图一长这样:
2.2梯度下降
在这一部分中,您将使用梯度下降将线性回归参数θ拟合到我们的数据集。
2.2.1 更新方程
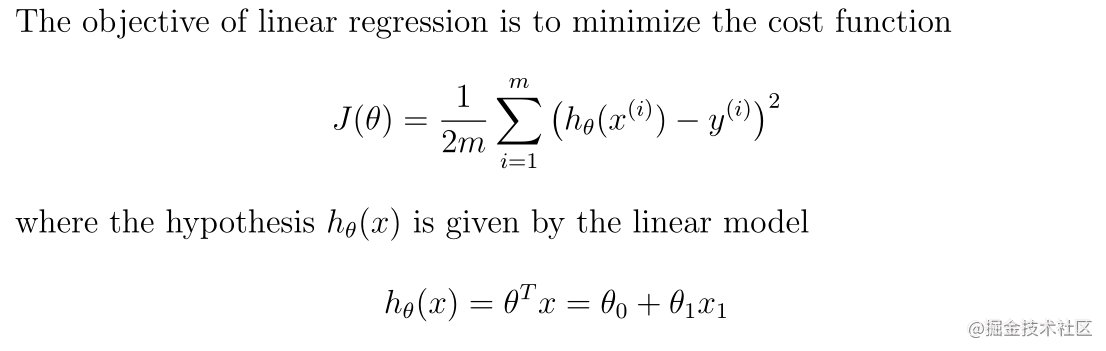
线性回归的目标是最小化成本函数:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
h θ ( x ) = θ T x = θ 0 + θ 1 x 1 h_{\theta}(x)=\theta^{T} x=\theta_{0}+\theta_{1} x_{1} hθ(x)=θTx=θ0+θ1x1


回想一下,模型的参数是 θ j θ_j θj。这些是您将调整以最小化成本 J ( θ ) J(θ) J(θ)的值。一种方法是使用批量梯度下降算法。在批量梯度下降中,每次迭代都执行更新
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
随着梯度下降的每一步,你的参数θ越来越接近最佳值,将实现最低的成本J(θ)。

注意:我们在Octave/MATLAB中把每个例子存储为X矩阵中的一行。为了考虑截距项 θ 0 θ_0 θ0,我们在X上增加一个额外的第一列,并将其设置为全1。这让我们可以将 θ 0 θ_0 θ0简单地视为另一个“特征”。
2.2.2 实现

在ex1.m中,我们已经为线性回归载入了数据。下面几行代码中我们向数据中添加了一列1作为 θ 0 \theta_0 θ0。我们还将初始参数初始化为θ,并将学习速率α初始化为0.01。
2.2.3 计算代价函数J(θ)

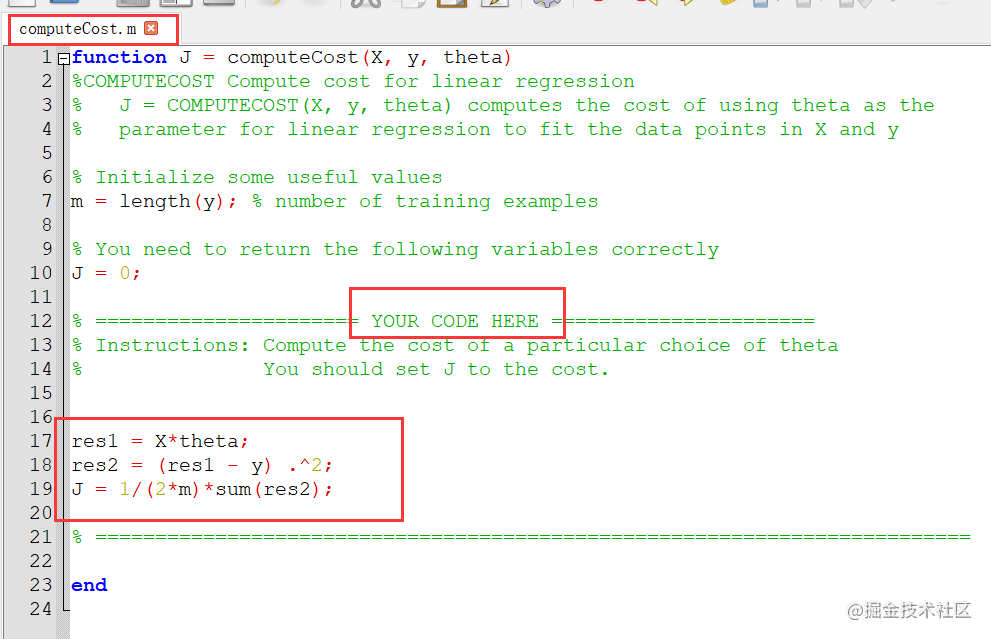
当执行梯度下降来最小化代价函数J(θ)时,通过计算成本来监控收敛是有帮助的。在本节中,你要实现一个计算J(θ)的函数,以便检查梯度下降实现的收敛性。完成文件computeCost.m中的代码,这是一个计算J(θ)的函数。完成后,ex1.m中下一步执行computeCost,将θ初始化为零向量。输出32.07英镑结果正确的。
在这个文件里写上我下边的这段代码。
hx = X*theta;
J = 1/(2*m)*sum((hx - y) .^2);
hx = X*theta;- X是两列的矩阵,第一列是1,第二列是城市人口
- theta是一个列向量,分别是 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1
- X*theta结果就是一个列向量,用hx存储h(x)预测结果
- 就是利用矩阵和向量相乘 θ T x \theta^{T} x θTx,求出 h θ ( x ) = θ T x = θ 0 + θ 1 x 1 h_{\theta}(x)=\theta^{T} x=\theta_{0}+\theta_{1} x_{1} hθ(x)=θTx=θ0+θ1x1
(hx - y) .^2- hx存储的h(x)减去y
- 计算的是这一步 h θ ( x ( i ) ) − y ( i ) h_{\theta}\left(x^{(i)}\right)-y^{(i)} hθ(x(i))−y(i)
J = 1/(2*m)*sum((hx - y) .^2);- J是函数的返回值
- 计算完整公式
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}
2m1∑i=1m(hθ(x(i))−y(i))2
在octave里运行之后如下,可见零向量那个测试数据结果确实是32.07,这一步也成功啦。!

2.2.4 梯度下降

接下来,在文件gradientDescent.m中实现梯度下降。循环结构已经写好了,只需要在每次迭代中提供对θ的更新。(就是让你写θ的值。)
代码如下:
hx = X * theta;
theta(1) = theta(1) - alpha*(1/m)*sum((hx-y) .* X(:,1:1));
theta(2) = theta(2) - alpha*(1/m)*sum((hx-y) .* X(:,2:2));
由于上边代价函数那里解释的很详细,所以这里就只写公式。(应该能看懂吧?看不懂再问)
hx = X * theta;- h θ ( x ) h_{\theta}(x) hθ(x)
theta(1) = theta(1) - alpha*(1/m)*sum((hx-y) .* X(:,1:1));- θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 1 ( i ) \theta_{1}:=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_1^{(i)} θ1:=θ1−αm1∑i=1m(hθ(x(i))−y(i))x1(i)
theta(2) = theta(2) - alpha*(1/m)*sum((hx-y) .* X(:,2:2));- θ 2 : = θ 2 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 2 ( i ) \theta_{2}:=\theta_{2}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_2^{(i)} θ2:=θ2−αm1∑i=1m(hθ(x(i))−y(i))x2(i)

最后会出来一个图像长这样:

如果你的图像没有散点图只有一个斜线,那问题就出在,显示第一张图像(散点图)被你关闭了,不关掉那张图就显示正常了。
2.3 调试
梯度下降时,需要记住以下几点:

Octave/MATLAB数组索引从1开始,而不是从0开始。和别的语言不太一样,注意区分,

这条是说矩阵维度的问题,如果报错了看看错误信息写的是啥,别只看到一个error就不动了,看看的后边错误信息有什么,都会写的很清楚你错在哪里。

如果一直出错不知道问题出在哪里,看看你是不是搞混了数学运算符和矩阵运算符。
2.4 可视化J(θ)

为了更好地理解代价函数J(θ),继续往下会生成代价函数的图像,一个二维一个三维。


在ex1.m的下一步中,下边框框里的代码就是使用你编写的computeCost函数在值网格上计算J(θ)。

执行这些行后,您将得到一个J(θ)的二维数组。然后ex1.m使用surf和contour命令,使用这些值生成J(θ)的曲面和等高线图,见图3:
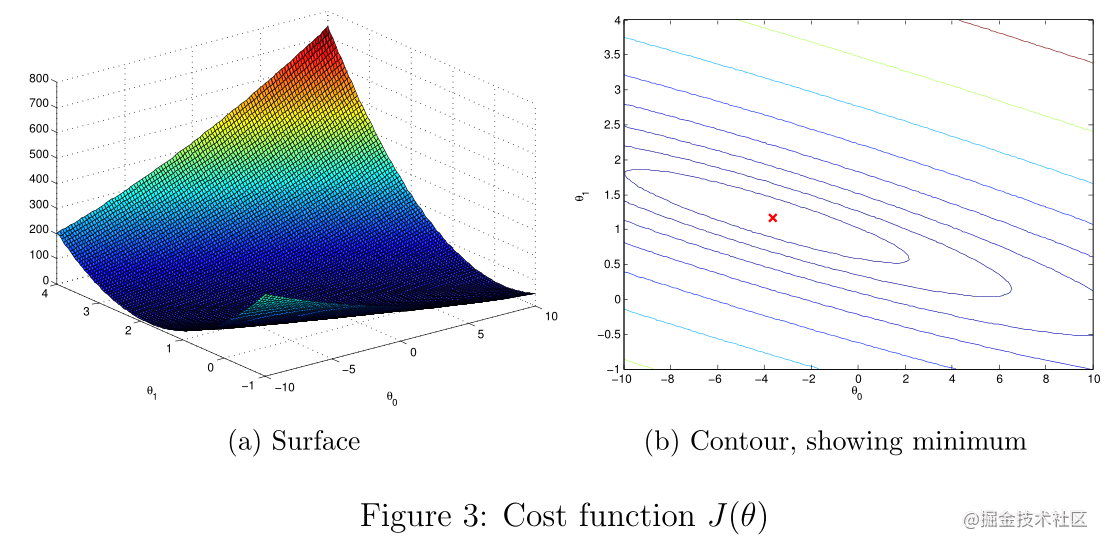

如图可以了解J(θ)如何随着 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1的变化而变化。成本函数J(θ)是碗形的,具有全局最小值。这个最小值是 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1的最优解,梯度下降的每一步都向这个点靠近。

最后提交一下子,做的这三个都是正确的。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










