【笔记】最大全0 or 1子矩阵

类型题正解悬线法。。。原谅我不深入去研究只是草草的水水二维前缀和与单调栈w
这个最大全类型子矩阵，，先姑且当做刷脸攒RP的内容学习吧w

对于二维前缀和版本的还是比较喜欢，而且看了些大佬的博客也觉得超好，尤其是有图有真相那种
但是感觉悬线法动起来真的好容易看懂，推荐大家有空时候看看2333

最大全零子矩阵

部分引用自大佬博客

http://blog.csdn.net/qq_35264769/article/details/53066287

这个题可以预处理矩阵前缀和然后用n^3的方法解决，可是明显会超时，所以有一种n^2的算法。
我们可以一行一行的去算，设h[j]为从当前行开始向上数连续的0的个数（当前第i行也为0），如果当前位置等于1的话那么h[j]=0。
比如说样例：

5
0 1 0 1 0
0 0 0 0 0
0 0 0 0 1
1 0 0 0 0
0 1 0 0 0
那么每个位置的h[j]为
1 0 1 0 1
2 1 2 1 2
3 2 2 2 0
0 3 4 3 1
1 0 5 4 2
然后我们在求出来每一行h[j]的同时，去找当前位置可以到达的左边界和右边界。我们设l[j]，r[j]为左右边界。我们设l[j],r[j]初始值都为j。显然，如果h[j]<=h[l[j]-1],那么l[j]=l[l[j]-1]；对应着，如果h[j]<=h[r[j]+1],那么r[j]=r[r[j]+1];
我们来举个例子；






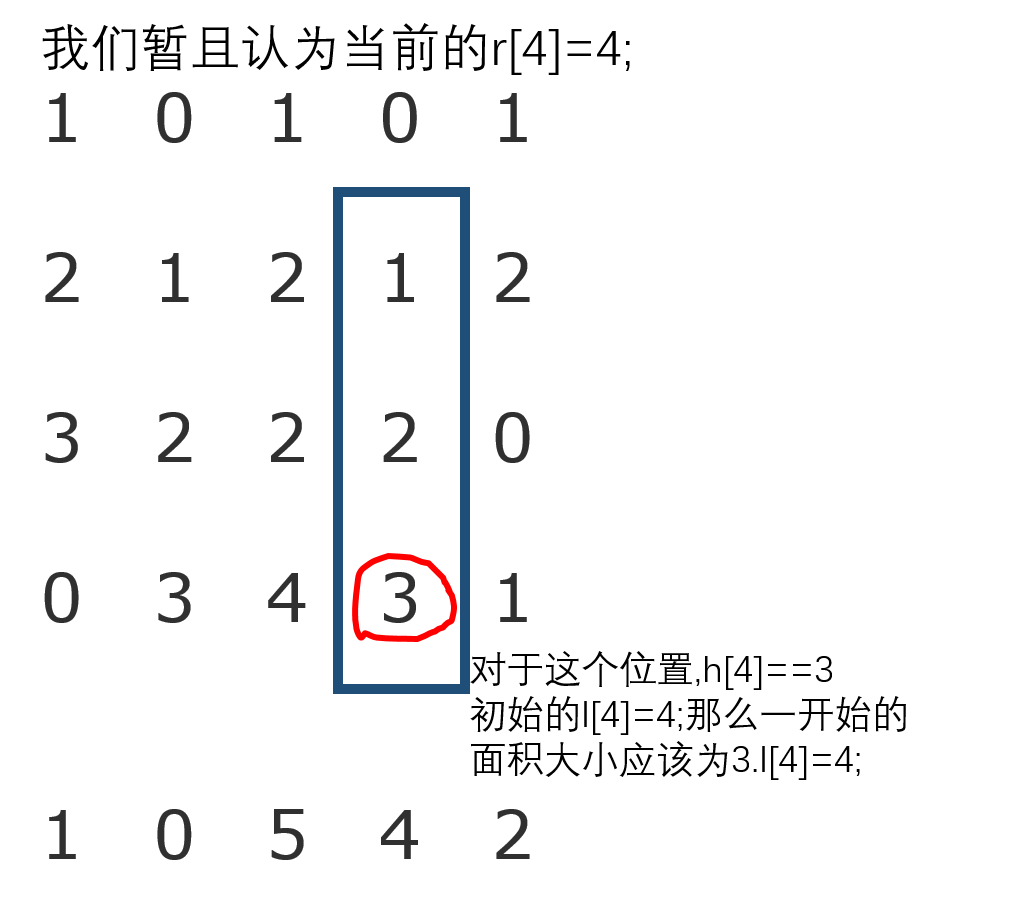
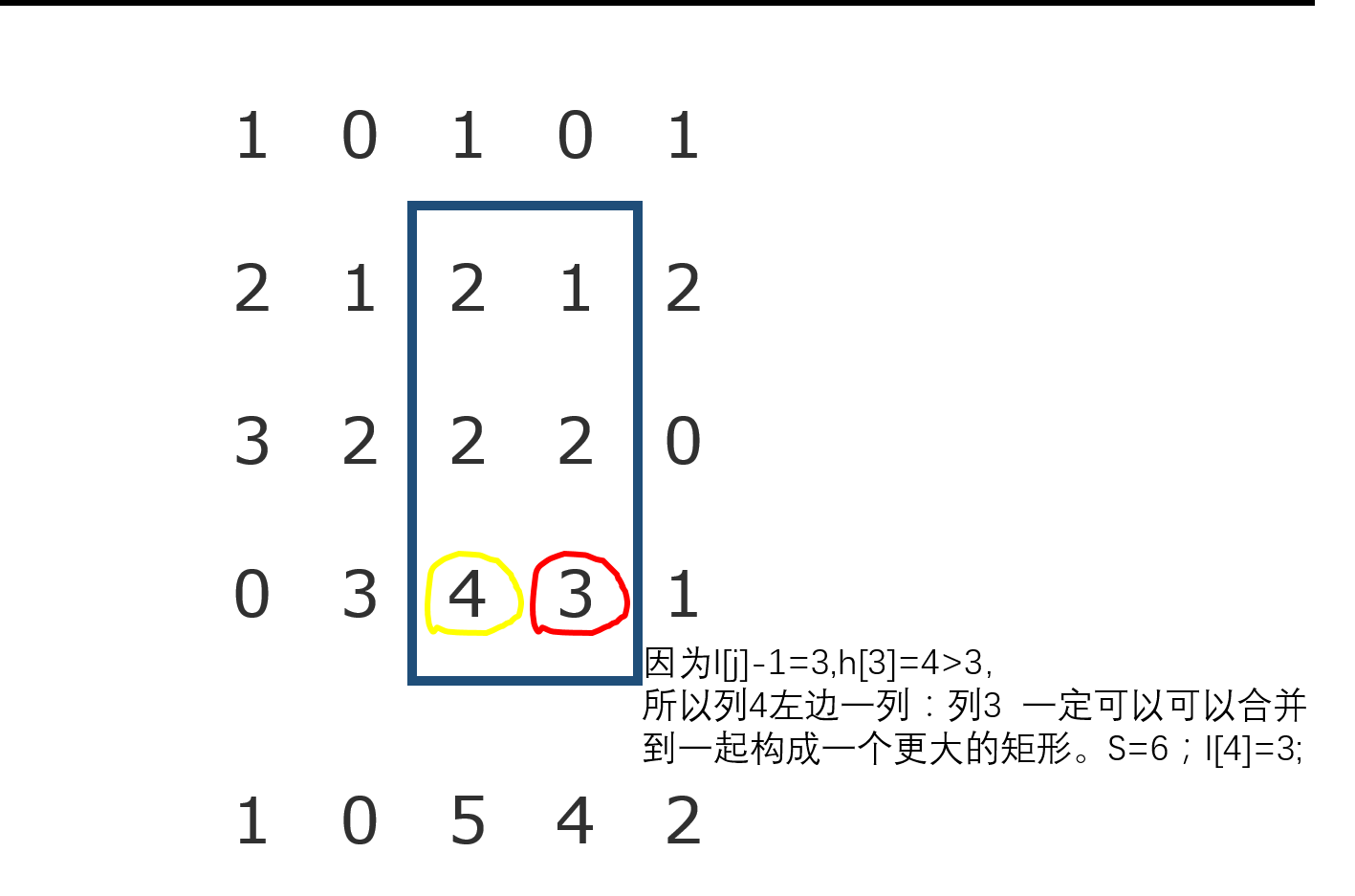
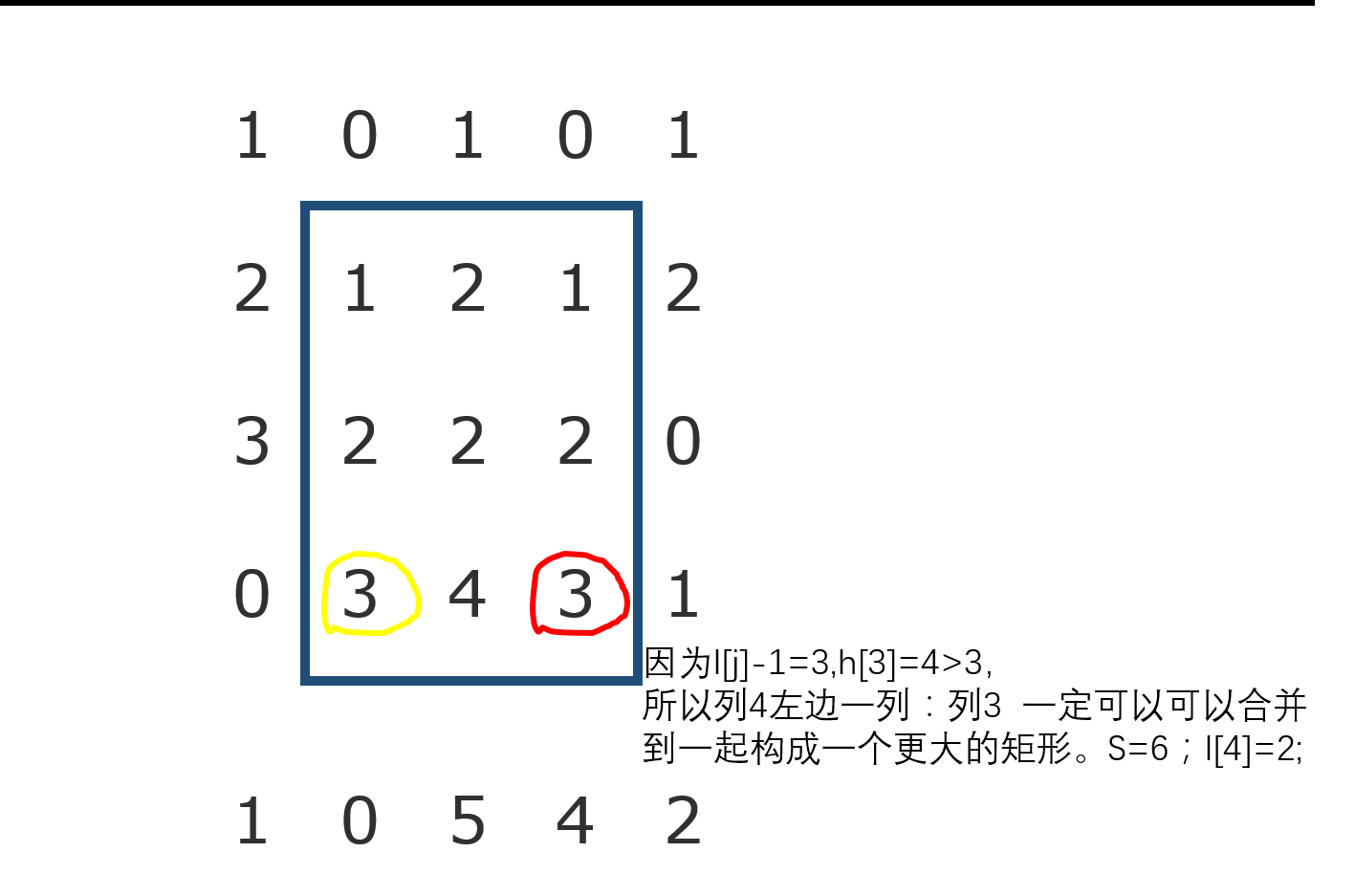
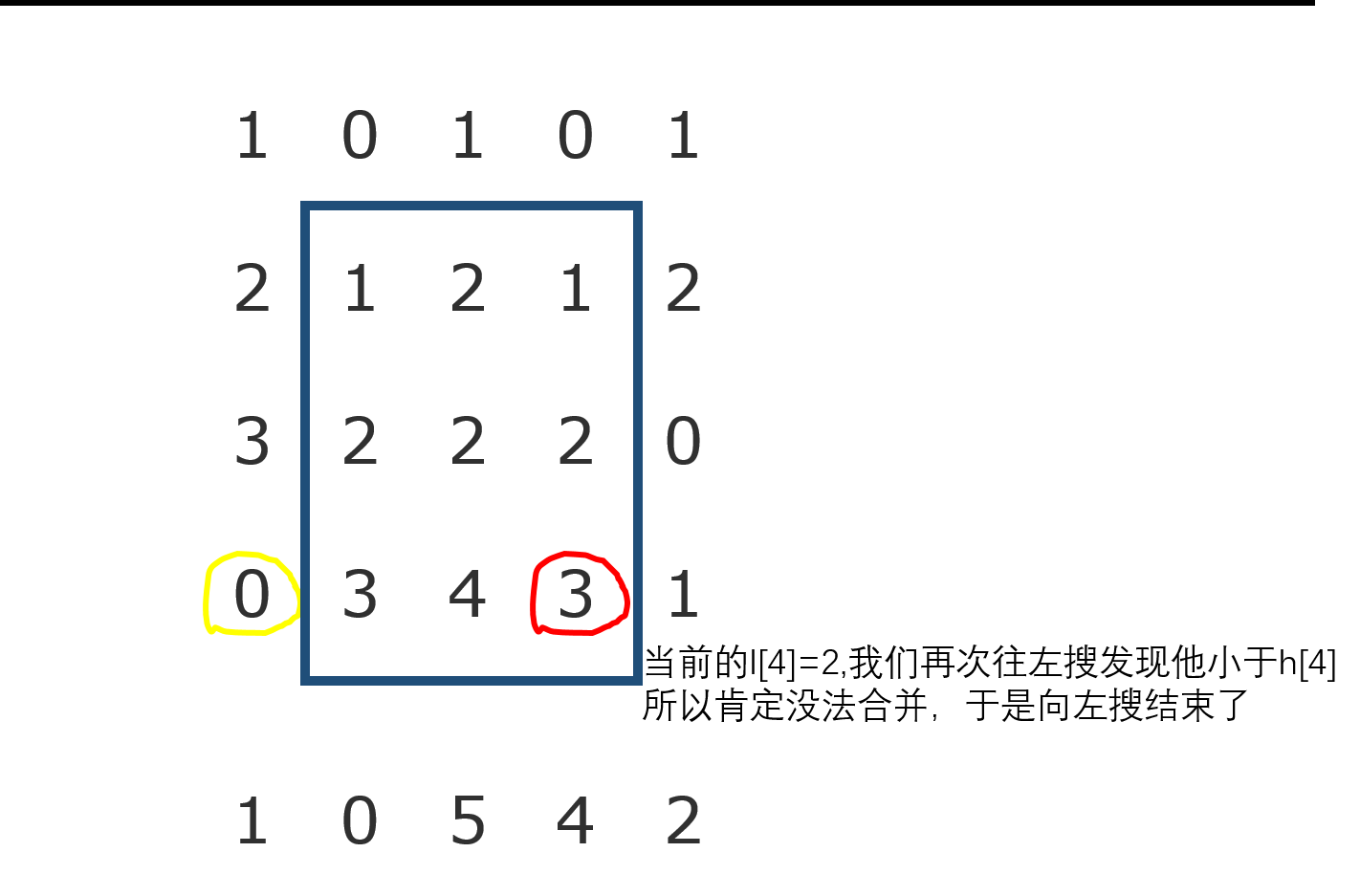
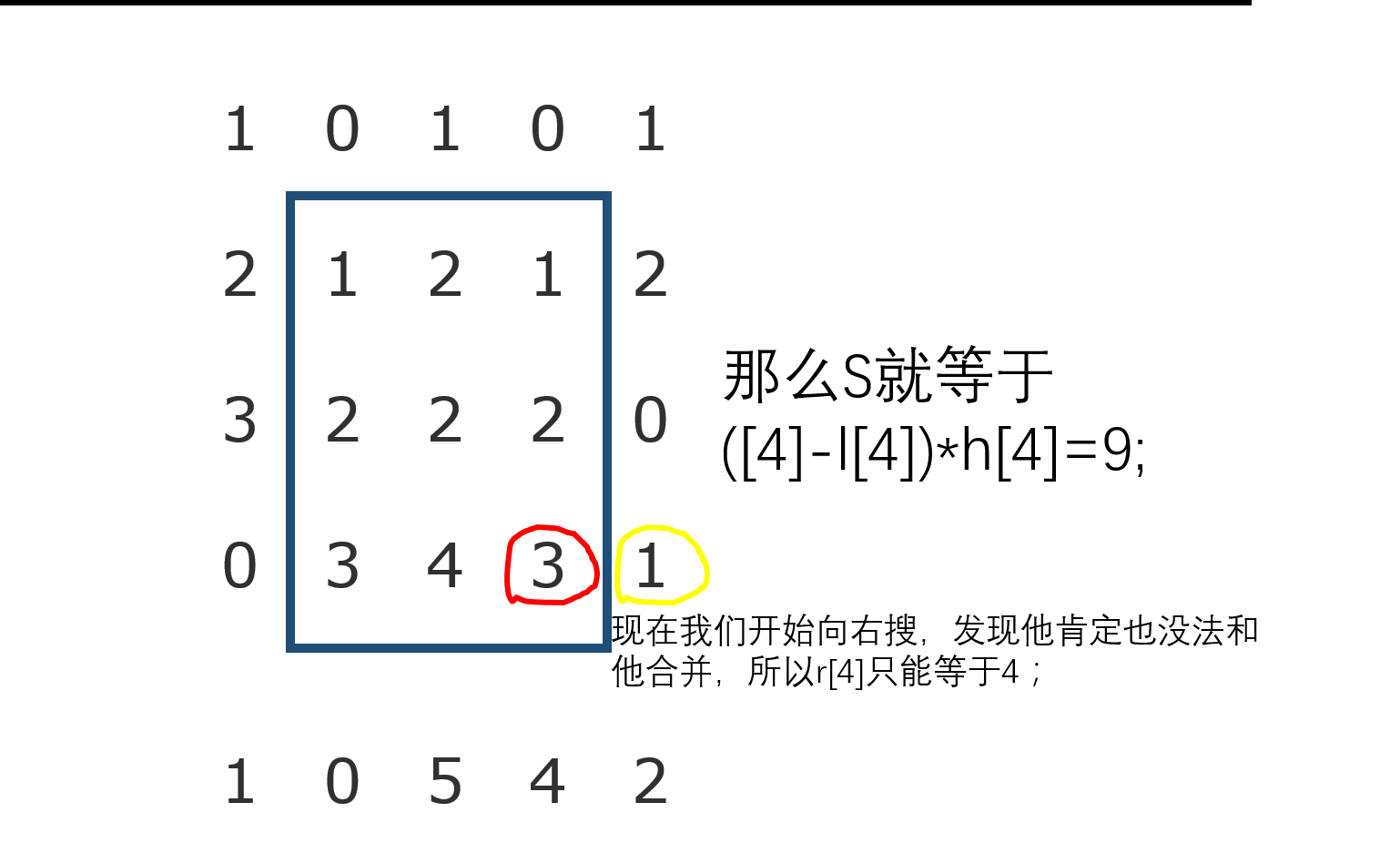
还有一个要注意的问题，因为到每一行的时候，h[j]都会跟着更新，所以我们每次求出来h[j]的时候应该紧跟着去求他的l和r，并且算面积。

#include<cstdio> 
#include<iostream>
#include<algorithm>
using namespace std;
const int sz = 2100;
int n,h[sz],map[sz][sz],l[sz],r[sz],ans;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
        cin>>map[i][j];
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {//一行一行处理，h[j]存储的是到第i行时，在第j列从i行开始往上的0的个数  
            if(map[i][j]==0)//此处改为1则变成最大全1子矩阵 
                h[j]++;
            else
                h[j]=0;
        }
        for(int j=1;j<=n;j++)
        {//每一行都要去算
            l[j]=j;
            while(l[j]>1&&h[j]<=h[l[j]-1])
                l[j]=l[l[j]-1];//如果能够扩展就向左扩展
        }
        for(int j=n;j>=1;j--)
        {//注意这里要从右向左，因为我们是根据右边的更新左边的
            r[j]=j;
            while(r[j]<n&&h[j]<=h[r[j]+1])
                r[j]=r[r[j]+1];
        } 
        for(int j=1;j<=n;j++)
            ans=max(h[j]*(r[j]-l[j]+1),ans);
    }
    cout<<ans<<endl;
    return 0; 
}

上面这个版本是我很喜欢的版本，主要是因为不会单调栈2333

下面是一位单调栈大佬的博客

http://www.cnblogs.com/shadowwalker9/p/6002878.html

http://www.cnblogs.com/fstang/archive/2013/05/19/3087746.html

这里的代码没有使用单调栈的方法：

题目：http://ac.jobdu.com/problem.php?cid=1045&pid=0

题目描述：

在一个M * N的矩阵中，所有的元素只有0和1，从这个矩阵中找出一个面积最大的全1子矩阵，所谓最大是指元素1的个数最多。

输入：

输入可能包含多个测试样例。
对于每个测试案例，输入的第一行是两个整数m、n(1<=m、n<=1000)：代表将要输入的矩阵的大小。
矩阵共有m行，每行有n个整数，分别是0或1，相邻两数之间严格用一个空格隔开。

输出：

对应每个测试案例，输出矩阵中面积最大的全1子矩阵的元素个数。

样例输入：

2 2
0 0
0 0
4 4
0 0 0 0
0 1 1 0
0 1 1 0
0 0 0 0

样例输出：

0
4

方法是：

1、先将0/1矩阵读入x，对每一个非零元素x[i][j]，将其更新为：在本行，它前面的连续的1的个数+1（+1表示算入自身）

　　比如，若某一行为0 1 1 0 1 1 1，则更新为0 1 2 0 1 2 3

2、对每一个非零元素x[i][j]，在第j列向上和向下扫描，直到遇到比自身小的数，若扫描了y行，则得到一个大小为x[i][j]*(y+1)的全1子矩阵（+1表示算入自身所在行）

　　比如，若某一列为[0 3 4 3 5 2 1]’(方便起见，这里将列表示成一个列向量)，我们处理这一列的第4个元素，也就是3，它向上可以扫描2个元素，向下可以扫描1个元素，于是得到一个4×3的全1子矩阵。

3、在这些数值中取一个最大的。

思想大概如下图所示（空白处的0没有标出）

对照步骤2中给出的例子，蓝色的箭头表示向上向下扫描，黑色的框表示最终得到的全1子矩阵

这样做为什么是对的？

想一想，对那个最大的全1子矩阵，用这种方法能不能找到它呢？——肯定可以。

一个最大全1子矩阵，肯定是四个边界中的每一个都不能再扩展了，如下图

假设图中全1子矩阵就是最大子矩阵，则左边界左侧那一列肯定有一个或多个0（否则就可以向左边扩展一列，得到一个更大的全1矩阵）

对其他3个边界有类似的情况。

然后看图中用黑圈标出的1（其特点是：和左边界左侧的某个0在同一行），从这个1出发，按照之前的方法，向上向下扫描，就可以得到这个子矩阵。所以，肯定可以找到。

下面是我的代码，实际实现的时候，为了提高效率，估计了一下upperbound，这个upperbound就是：在当前列，

包含x[i][col]的连续的非零序列的和，比如对某列[0 3 4 3 5 2 1]’，后面6个的upperbound都是
3 + 4 + 3 + 5 + 2 + 1 = 18，对于0元素，不需要upperbound

 

#include <stdio.h>
int m, n;
int x[1002][1002];
int upperbound[1002][1002];
//pre处理后，x[i][j]表示原矩阵第i行中x[i][j]前面有多少个连续的1
void pre() {
    for (int i = 0; i < m; i++) {
        for (int j = 1; j < n; j++) {//注意，j从1开始
            //每行第一个元素不用判断，0/1都不用改变,对应每一段的第一个1也是如此
            if (x[i][j] == 1 && x[i][j - 1] != 0) {
                x[i][j] = x[i][j - 1] + 1;
            }
        }
    }
}
//proc_col对第col列计算每个x[i][col]的upperbound，这个upperbound就是：在当前列，
//包含x[i][col]的连续的非零序列的和，比如对[0 3 4 3 5 2 1]，后面6个的upperbound都是
//3 + 4 + 3 + 5 + 2 + 1 = 18，对于0元素，不需要upperbound
void proc_col(int col) {
    for (int i = 0; i < m; i++) {
        if (x[i][col] == 0) {
            continue;
        }
        int sum = 0, j = i;
        while (j < m && x[j][col] > 0) {
            sum += x[j][col];
            j++;
        }
        for (int k = i; k < j; k++) {
            upperbound[k][col] = sum;
        }
        i = j;//之后i还会++，但是不会跳过重要的值，因为此时x[j][]=0或在界外
    }
}
//逐列计算upperbound
void calc_upper(){
    for (int col = 0; col < n; col++) {
        proc_col(col);
    }
}
//从x[row][col]向上向下扫描
int search_up_down(int row, int col) {
    int cnt = 1, val = x[row][col];
    for (int i = row - 1; i >= 0; i--) {
        if (x[i][col] >= val) {
            cnt++;
        } else {
            break;
        }
    }
    for (int i = row + 1; i < m; i++) {
        if (x[i][col] >= val) {
            cnt++;
        } else {
            break;
        }
    }
    return cnt * val;
}
//得到最大全1子矩阵的大小
int getMax() {
    int max = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (x[i][j] != 0 && max < upperbound[i][j]) {
                int val = search_up_down(i, j);
                if (val > max) {
                    max = val;
                }
            }
        }
    }
    return max;
}
int main(int argc, const char *argv[])
{
    while(scanf("%d%d", &m, &n) != EOF) {
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                scanf("%d", &x[i][j]);
            }
        }
        pre();
        calc_upper();
        printf("%d\n", getMax());
    }
    return 0;
}

 

单调栈的介绍：

http://www.cnblogs.com/ziyi–caolu/archive/2013/06/23/3151556.html

这里并不完备，有时间应当自己实现一下。

目前想到的最容易理解的方法是遍历两遍，从左往右，从右往左。每次都记录弹出的元素，和弹出元素本身计算出来的值。

两次逆序相加即可。(具体可以根据例子验证)