1. 八皇后问题
八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。计算机发明后,有多种计算机语言可以解决此问题。
八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。
八皇后问题的第一个解是在1850年由弗朗兹·诺克给出的。诺克也是首先将问题推广到更一般的n皇后摆放问题的人之一。1874年,S.冈德尔提出了一个通过行列式来求解的方法,这个方法后来又被J.W.L.格莱舍加以改进。
艾兹格·迪杰斯特拉在1972年用这个问题为例来说明他所谓结构性编程的能力。
八皇后问题出现在1990年代初期的著名电子游戏第七访客中。
在8*8国际象棋棋盘上,要求在每一行放置一个皇后,且能做到在竖方向,斜方向都没有冲突。国际象棋的棋盘如下图1所示:
2. 基本思路
基本思路采用逐步试探的方式,先从一个方向往前走,能进则进,不能进则退,尝试另外的路径,类似迷宫。首先我们来分析一下国际象棋的规则,这些规则能够限制我们的前进,也就是我们前进途中的障碍物。一个皇后q(x,y)能被满足以下条件的皇后q(row,col)吃掉
1)x=row(在纵向不能有两个皇后)
2) y=col(横向)
3)col + row = y+x;(斜向正方向)
4) col - row = y-x;(斜向反方向)
遇到上述问题之一的时候,说明我们已经遇到了障碍,不能继续向前了。我们需要退回来,尝试其他路径。
我们将棋盘看作是一个8*8的数组,这样可以使用一种蛮干的思路去解决这个问题,这样我们就是在8*8=64个格子中取出8个的组合,C(64,80) = 4426165368,显然这个数非常大,在蛮干的基础上我们可以增加回溯,从第0列开始,我们逐列进行,从第0行到第7行找到一个不受任何已经现有皇后攻击的位置,而第五列,我们会发现找不到皇后的安全位置了,前面四列的摆放如下:
第五列的时候,摆放任何行都会上图所示已经存在的皇后的攻击,这时候我们认为我们撞了南墙了,是回头的时候了,我们后退一列,将原来摆放在第四列的皇后(3,4)拿走,从(3,4)这个位置开始,我们再第四列中寻找下一个安全位置为(7,4),再继续到第五列,发现第五列仍然没有安全位置,回溯到第四列,此时第四列也是一个死胡同了,我们再回溯到第三列,这样前进几步,回退一步,最终直到在第8列上找到一个安全位置(成功)或者第一列已经是死胡同,但是第8列仍然没有找到安全位置为止
用回溯的方法解决8皇后问题的步骤为:
1)从第一列开始,为皇后找到安全位置,然后跳到下一列
2)如果在第n列出现死胡同,如果该列为第一列,棋局失败,否则后退到上一列,在进行回溯
3)如果在第8列上找到了安全位置,则棋局成功。
回溯就是对栈的使用,后入先出。
3. 功能函数
基本算法同上面描述,先在[0,0]位置放置一个皇后,数组queue表示每列放置皇后的位置,共8列。在[0,0]放完皇后后,queue的值就是{0,0,0,0,0,0,0,0},在第二列第二排放完皇后后,queue值就是{0,1,0,0,0,0,0,0}了。
判断是否能放的函数是
for(i = 0; i < n; i++)
{
if(queen[i]== queen[n] || abs(queen[i] - queen[n]) == (n - i))
{
return1;
}
}
此处i是从0到n循环检测,就是从第一行检测到第n行。如果相等queen[i] == queen[n],说明在同一行了,肯定不满足条件。abs(queen[i] - queen[n]) == (n - i) 表示在同一条斜线上,也不满足条件。
如果整列不满足放置皇后的条件,则进行回溯。其实当放完8个皇后成功后也是进行的回溯操作。
4. Main函数
先初始化棋盘,
初始化棋盘每个地方都为空心,放置棋盘的地方都是实心。
注意这个算法时间复杂度度比较高,棋盘规模调大,小心机器计算时间太长。
int main()
{
int iLine,iColumn; /* 行 列*/
/*初始化棋盘*/
for (iLine=0;iLine <max;iLine++){
for (iColumn=0;iColumn <max;iColumn++){
Queen[iLine][iColumn] = 1;
}
}
put(0);/*从横坐标为0开始依次尝试*/
printf("theresult is = %d\n", sum);
return0;
}
最后如下图所示:
5. 源码
#include<stdio.h>
#include<stdlib.h>
#definemax 8
int queen[max],sum=0; /* max为棋盘最大坐标*/
int Queen[max][max];
/*输出棋盘状态*/
void show_graph()
{
int iLine,iColumn;
for (iLine=0;iLine <max;iLine++){
for (iColumn=0;iColumn <max;iColumn++){
printf("%c",Queen[iLine][iColumn]);
}
printf("\n");
}
printf("\n");
sum++;
}
void show() /* 输出所有皇后的坐标 */
{
inti;
for(i= 0; i < max; i++)
{
printf("(%d,%d)", i, queen[i]);
}
printf("\n");
sum++;
}
int check(intn) /*检查当前列能否放置皇后 */
{
inti;
for(i= 0; i < n; i++) /* 检查横排和对角线上是否可以放置皇后 */
{
if(queen[i]== queen[n] || abs(queen[i] - queen[n])== (n - i))
{
return1;
}
}
return0;
}
void put(intn) /*回溯尝试皇后位置,n为横坐标 */
{
inti;
for(i= 0; i < max; i++)
{
queen[n]= i; /* 将皇后摆到当前循环到的位置*/
Queen[n][i]=2;//二维数组
if(!check(n))
{
if(n== max - 1)
{
//show();/* 如果全部摆好,则输出所有皇后的坐标*/
show_graph();
}
else
{
put(n +1); /* 否则继续摆放下一个皇后*/
}
}
Queen[n][i]=1;//二维数组
}
}
int main()
{
int iLine,iColumn; /* 行 列*/
/*初始化棋盘*/
for (iLine=0;iLine <max;iLine++){
for (iColumn=0;iColumn <max;iColumn++){
Queen[iLine][iColumn] = 1;
}
}
put(0);/*从横坐标为0开始依次尝试*/
printf("theresult is = %d\n", sum);
return0;
}
弗洛伊德(Floyd)算法是解决任意两点间的最短路径的一种算法,可以正确处理有向图或有向图或负权(但不可存在负权回路)的最短路径问题,同时也被用于计算有向图的传递闭包。
算法思想与过程
(一)算法思想:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)。
从任意节点i到任意节点j的最短路径不外乎2种可能,一是直接从i到j,二是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
(二)算法过程
1)首先把初始化距离dist数组为图的邻接矩阵,路径数组path初始化为-1。其中对于邻接矩阵中的数首先初始化为正无穷,如果两个顶点存在边则初始化为权重
2)对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是就更新它。
状态转移方程为
如果 dist[i][k]+dist[k][j] < dist[i][j]
则dist[i][j] = dist[i][k]+dist[k][j]
bool Floyd(){
for(int k = 1 ; k < this->Nv+1 ; k++){
for(int i = 1 ; i < this->Nv+1 ; i++){
for(int j = 1 ; j < this->Nv+1 ; j++){
if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){
this->dist[i][j] = this->dist[i][k] + this->dist[k][j];
if(i == j && this->dist[i][j] < 0){
return false;
}
this->path[i][j] = k;
}
}
}
}
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
例子
我们用如下图结构来演示Floyd算法:
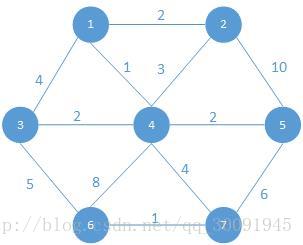
全部代码为:
#include <iostream>
#include <cstring>
#include <stack>
#include <queue>
using namespace std;
const int MAX = 65535;
class Graph{
private:
int** G;
int** dist;
int** path;
int Nv;
public:
Graph(int nv, int ne){
this->Nv = nv;
G = new int*[nv+1];
dist = new int*[nv+1];
path = new int*[nv+1];
for(int i = 0 ; i < nv+1 ; i++){
G[i] = new int[nv+1];
dist[i] = new int[nv+1];
path[i] = new int[nv+1];
memset(path[i],-1,sizeof(path[0][0])*(nv+1));
for(int j = 0 ; j < nv+1 ; j++){
this->G[i][j] = this->dist[i][j] = MAX;
}
}
cout<<"请输入边与权重:"<<endl;
for(int i = 0 ; i < ne ; i++){
int v1,v2,weight;
cin>>v1>>v2>>weight;
this->G[v1][v2] = this->G[v2][v1] = weight;
this->dist[v1][v2] = this->dist[v2][v1] = weight;
}
}
bool Floyd(){
for(int k = 1 ; k < this->Nv+1 ; k++){
for(int i = 1 ; i < this->Nv+1 ; i++){
for(int j = 1 ; j < this->Nv+1 ; j++){
if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){
this->dist[i][j] = this->dist[i][k] + this->dist[k][j];
if(i == j && this->dist[i][j] < 0){
return false;
}
this->path[i][j] = k;
}
}
}
}
return true;
}
void Print_Path(int start,int end){
stack<int> stack;
queue<int> queue;
int k = this->path[start][end];
int tmp = k;
if(k == -1){
cout<<start<<"->"<<end<<endl;
return;
}
stack.push(k);
while(this->path[start][k] != -1){
stack.push(this->path[start][k]);
k = this->path[start][k];
}
stack.push(start);
while(this->path[tmp][end] != -1){
queue.push(this->path[tmp][end]);
tmp = this->path[tmp][end];
}
queue.push(end);
cout<<stack.top();
stack.pop();
while(!stack.empty()){
cout<<"->"<<stack.top();
stack.pop();
}
while(!queue.empty()){
cout<<"->"<<queue.front();
queue.pop();
}
cout<<endl;
}
void Print_Floyd(){
int i,j,k;
cout<<" length path"<<endl;
for(i = 1 ; i < this->Nv+1 ; i++){
for(j = i+1 ; j < this->Nv+1 ; j++){
cout<<i<<"->"<<j<<" ";
cout<<this->dist[i][j]<<" ";
this->Print_Path(i,j);
}
cout<<endl;
}
}
};
int main()
{
cout<<"请输入顶点数与边长数:"<<endl;
int nv,ne;
cin>>nv>>ne;
Graph graph(nv,ne);
if(graph.Floyd()){
cout<<"各个顶点的最短路径为:"<<endl;
graph.Print_Floyd();
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
截图如下:
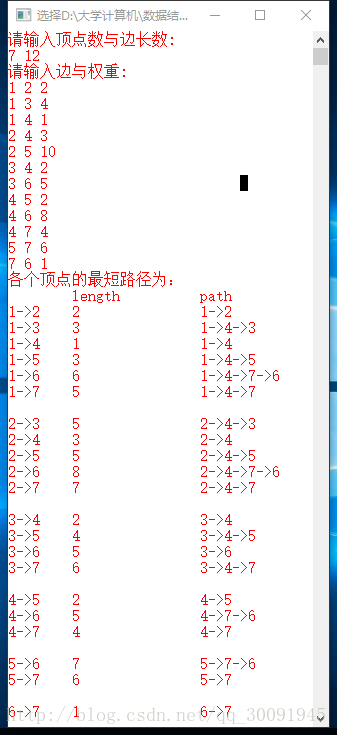
可以简化成如是描述:一个二维矩阵,每个点都有权重,需要找出从指定起点到终点的最短路径。
马上就想到了Dijkstra算法,所以又重新温故了一遍,这里给出Java的实现。
而输出最短路径的时候,在网上也进行了查阅,没发现什么标准的方法,于是在下面的实现中,我给出了一种能够想到的比较精简的方式:利用prev[]数组进行递归输出。
- package graph.dijsktra;
-
- import graph.model.Point;
-
- import java.util.*;
-
-
-
-
- public class Dijkstra {
- private int[][] map;
- private int[][] edges;
- private int[] prev;
- private boolean[] s;
- private int[] dist;
- private int pointNum;
- private Map<Integer, Point> indexPointMap;
- private Map<Point, Integer> pointIndexMap;
- private int v0;
- private Point startPoint;
- private Point endPoint;
- private Map<Point, Point> pointPointMap;
- private List<Point> allPoints;
- private int maxX;
- private int maxY;
-
- public Dijkstra(int map[][], Point startPoint, Point endPoint) {
- this.maxX = map.length;
- this.maxY = map[0].length;
- this.pointNum = maxX * maxY;
- this.map = map;
- this.startPoint = startPoint;
- this.endPoint = endPoint;
- init();
- dijkstra();
- }
-
-
-
-
- public void printShortestPath() {
- printDijkstra(pointIndexMap.get(endPoint));
- }
-
-
-
-
- private void init() {
-
- edges = new int[pointNum][pointNum];
- prev = new int[pointNum];
- s = new boolean[pointNum];
- dist = new int[pointNum];
- indexPointMap = new HashMap<>();
- pointIndexMap = new HashMap<>();
- pointPointMap = new HashMap<>();
- allPoints = new ArrayList<>();
-
-
- int count = 0;
- for (int x = 0; x < maxX; ++x) {
- for (int y = 0; y < maxY; ++y) {
- indexPointMap.put(count, new Point(x, y));
- pointIndexMap.put(new Point(x, y), count);
- count++;
- allPoints.add(new Point(x, y));
- pointPointMap.put(new Point(x, y), new Point(x, y, map[x][y]));
- }
- }
-
-
- for (int i = 0; i < pointNum; ++i) {
- for (int j = 0; j < pointNum; ++j) {
- if (i == j) {
- edges[i][j] = 0;
- } else {
- edges[i][j] = 9999;
- }
- }
- }
-
-
- for (Point point : allPoints) {
- for (Point aroundPoint : getAroundPoints(point)) {
- edges[pointIndexMap.get(point)][pointIndexMap.get(aroundPoint)] = aroundPoint.getValue();
- }
- }
-
- v0 = pointIndexMap.get(startPoint);
-
- for (int i = 0; i < pointNum; ++i) {
- dist[i] = edges[v0][i];
- if (dist[i] == 9999) {
-
-
- prev[i] = -1;
- } else {
-
- prev[i] = v0;
- }
- }
-
- dist[v0] = 0;
- s[v0] = true;
- }
-
-
-
-
- private void dijkstra() {
- for (int i = 1; i < pointNum; ++i) {
- int minDist = 9999;
- int u = v0;
-
- for (int j = 1; j < pointNum; ++j) {
- if (!s[j] && dist[j] < minDist) {
- u = j;
- minDist = dist[j];
- }
- }
- s[u] = true;
-
- for (int j = 1; j < pointNum; ++j) {
- if (!s[j] && edges[u][j] < 9999) {
- if (dist[u] + edges[u][j] < dist[j]) {
- dist[j] = dist[u] + edges[u][j];
- prev[j] = u;
- }
- }
- }
- }
- }
-
- private void printDijkstra(int endPointIndex) {
- if (endPointIndex == v0) {
- System.out.print(indexPointMap.get(v0) + ",");
- return;
- }
- printDijkstra(prev[endPointIndex]);
- System.out.print(indexPointMap.get(endPointIndex) + ",");
- }
-
- private List<Point> getAroundPoints(Point point) {
- List<Point> aroundPoints = new ArrayList<>();
- int x = point.getX();
- int y = point.getY();
- aroundPoints.add(pointPointMap.get(new Point(x - 1, y)));
- aroundPoints.add(pointPointMap.get(new Point(x, y + 1)));
- aroundPoints.add(pointPointMap.get(new Point(x + 1, y)));
- aroundPoints.add(pointPointMap.get(new Point(x, y - 1)));
- aroundPoints.removeAll(Collections.singleton(null));
- return aroundPoints;
- }
-
- public static void main(String[] args) {
- int map[][] = {
- {1, 2, 2, 2, 2, 2, 2},
- {1, 0, 2, 2, 0, 2, 2},
- {1, 2, 0, 2, 0, 2, 2},
- {1, 2, 2, 0, 2, 0, 2},
- {1, 2, 2, 2, 2, 2, 2},
- {1, 1, 1, 1, 1, 1, 1}
- };
- Point startPoint = new Point(0, 3);
- Point endPoint = new Point(5, 6);
- Dijkstra dijkstra = new Dijkstra(map, startPoint, endPoint);
- dijkstra.printShortestPath();
- }
- }
- package graph.model;
-
- public class Point {
- private int x;
- private int y;
- private int value;
-
- public Point(int x, int y) {
- this.x = x;
- this.y = y;
- }
-
- public Point(int x, int y, int value) {
- this.x = x;
- this.y = y;
- this.value = value;
- }
-
- public int getX() {
- return x;
- }
-
- public void setX(int x) {
- this.x = x;
- }
-
- public int getY() {
- return y;
- }
-
- public void setY(int y) {
- this.y = y;
- }
-
- public int getValue() {
- return value;
- }
-
- public void setValue(int value) {
- this.value = value;
- }
-
- @Override
- public String toString() {
- return "{" +
- "x=" + x +
- ", y=" + y +
- '}';
- }
-
- @Override
- public boolean equals(Object o) {
- if (this == o) return true;
- if (o == null || getClass() != o.getClass()) return false;
-
- Point point = (Point) o;
-
- if (x != point.x) return false;
- return y == point.y;
- }
-
- @Override
- public int hashCode() {
- int result = x;
- result = 31 * result + y;
- return result;
- }
- }
























 4124
4124

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








