【李航统计学笔记】Chap1：统计学习及监督学习概论

Chap1 都是些初步的概念，后续都有详细展开，在这里只对部分内容进行记录。

1 统计学习分类

1.1 基本分类

1.1.1 监督学习与无监督学习

pass

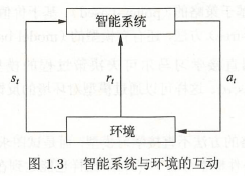
1.1.2 强化学习

1.1.3 半监督学习与主动学习

• 半监督学习（semi-supervised learning）：利用标注数据（少量）和未标注数据（大量）学习预测模型。利用未标注数据中的信息，辅助标注数据，进行监督学习，成本较低。
• 主动学习（active learning）：机器不断主动给出实例让人进行标注，然后利用标注数据学习预测模型。以较小的标注代价，达到较好的学习效果。

1.2 按算法分类

1.2.1 在线学习

• 在线学习（online learning）：每次接受一个样本，进行预测，之后学习模型，并不断重复该操作。
• 比批量学习难，每次模型更新中可用的数据有限难学到预测准确率更高的模型
• 适用场景：1）数据依次达到，无法存储，系统需及时处理。2）数据量很大，不能一次处理所有数据。3）数据的模式随时间动态变化，需要算法快速适应新模式。

1.2.2 批量学习

• 批量学习（batch learning）：一次接受所有数据，学习模型，之后进行预测

1.3 按模型分类

1.3.1 概率模型与非概率模型

• 概率模型（probabilistic model）：监督学习取条件概率分布形式P(y|x)，是生成模型；无监督学习取条件概率分布形式P(z|x)或P(x|z)。

  决策树、朴素贝叶斯、隐马尔可夫模型、条件随机场、概率潜在语义分析、潜在狄利克雷分配、高斯混合模型

• 非概率模型（non-probabilistic model）/确定性模型（deterministic model）：监督学习取函数形式y = f(x)，是判别模型；无监督学习取函数形式z = g(x)

  感知机、支持向量机、k近邻、AdaBoost、k均值、潜在语义分析、神经网络

1.3.2 线性模型与非线性模型

pass

1.3.3 参数化模型与非参数化模型

• 参数化模型（parametric model）：假设模型参数的维度固定，模型可以由有限维参数完全刻画。（适合问题简单的情况）
• 非参数化模型（non-parametric model）：假设模型参数的维度不固定或无穷大，随着训练数据量的增加而增大。（适合复杂问题，现实中常用）

2 各种概率与贝叶斯公式

看到一个信号发射的例子，感觉讲的非常好，终于理解了这一系列的概念。

2.1 问题描述

问题描述：
一个信号的发射端只发射A、B两种信号，其中发射信号A的概率为0.6，B概率为0.4。当发射信号A时，接收端接收到信号A的概率是0.9，接收到信号B的概率是0.1。当发射信号B时，接收端接收到信号B的概率为0.8，接收到信号A的概率为0.2。求当接收到信号A时，发射信号为A的概率。

发射信号为A的概率：$P(sendA)=0.6$
发射信号为B的概率：$P(sendB)=0.4$

发射信号A时，接收到信号A的概率：$P(receiveA|sendA)=0.9$
发射信号A时，接收到信号B的概率：$P(receiveB|sendA)=0.1$

发射信号B时，接收到信号B的概率：$P(receiv$