拉格朗日乘子法

搬运工
在求解最优化问题中，拉格朗日乘子法（Lagrange Multiplier）和KKT（Karush Kuhn Tucker）条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。

这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化，即最大值问题可以转化成最小值问题)。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法，不同之处在于应用的情形不同。

拉格朗日乘数法（Lagrange multiplier）有很直观的几何意义。举个2维的例子来说明：假设有自变量x和y，给定约束条件g(x,y)=c，要求f(x,y)在约束g下的极值。我们可以画出f的等高线图，如下图。此时，约束g=c由于只有一个自由度，因此也是图中的一条曲线（红色曲线所示）。显然地，当约束曲线g=c与某一条等高线f=d1相切时，函数f取得极值。两曲线相切等价于两曲线在切点处拥有共线的法向量。因此可得函数f(x,y)与g(x,y)在切点处的梯度（gradient）成正比。于是我们便可以列出方程组求解切点的坐标(x,y)，进而得到函数f的极值。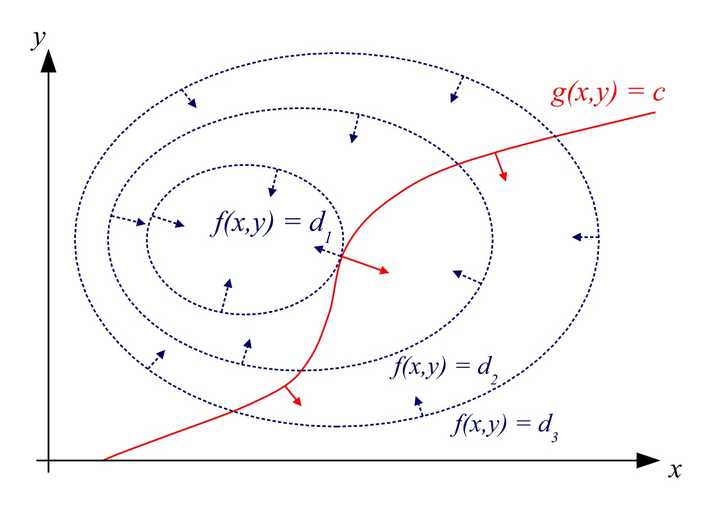
1 与原点的最短距离假如有方程：图像是这个样子滴：

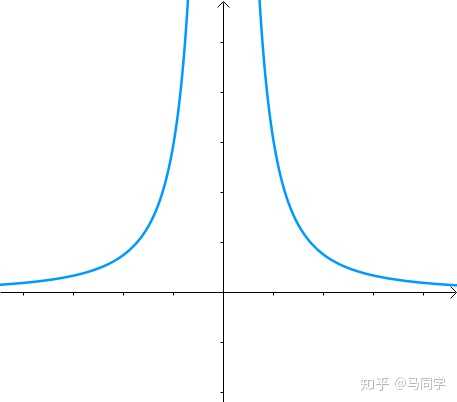
现在我们想求其上的点与原点的最短距离：

这里介绍一种解题思路。首先，与原点距离为 的点全部在半径为 的圆上：

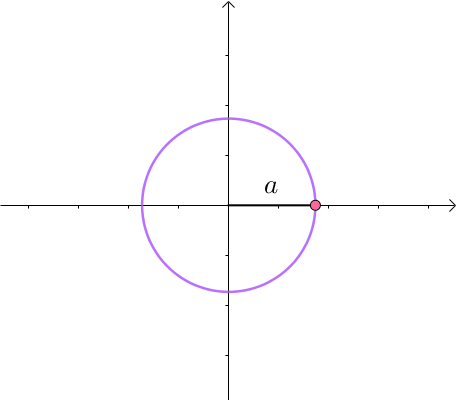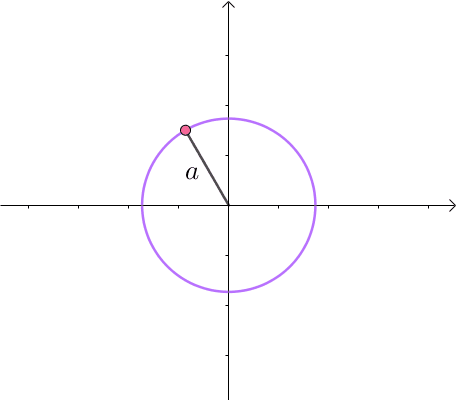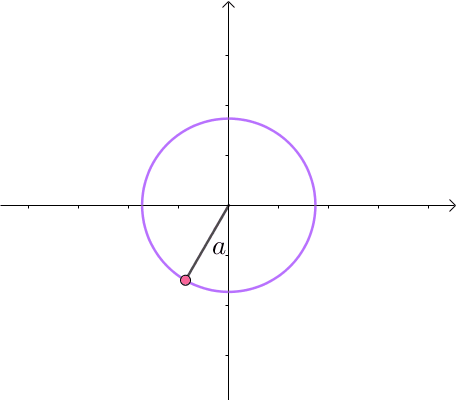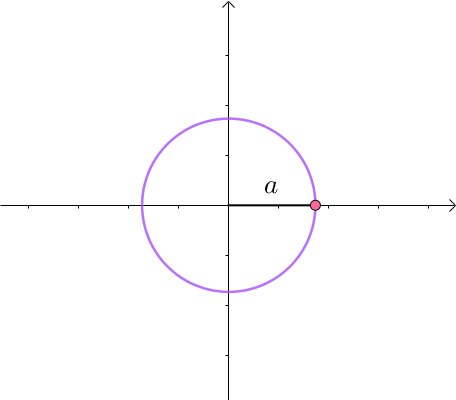
那么，我们逐渐扩大圆的半径：

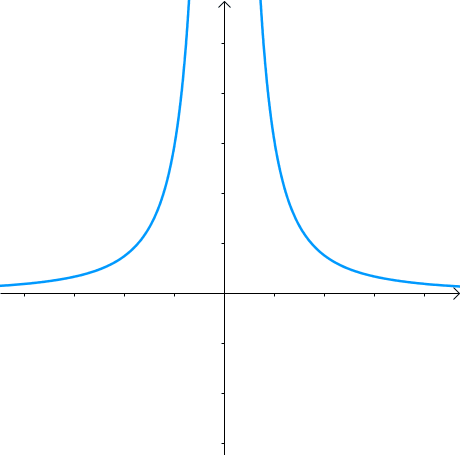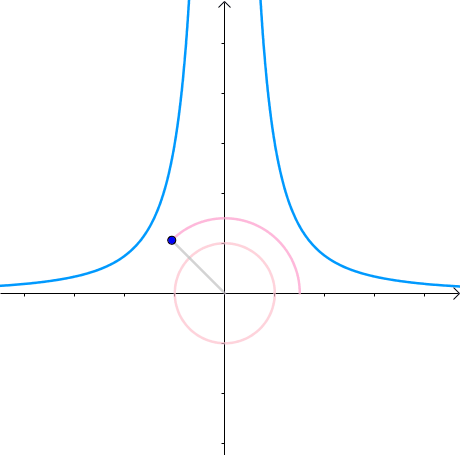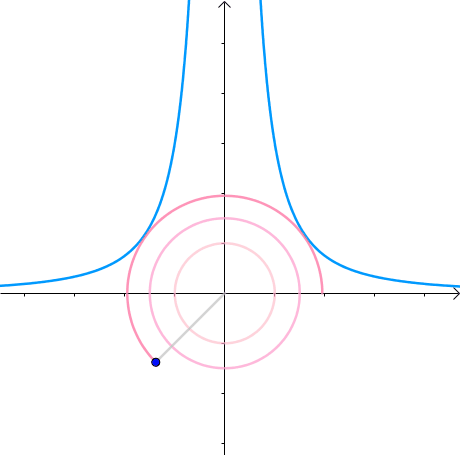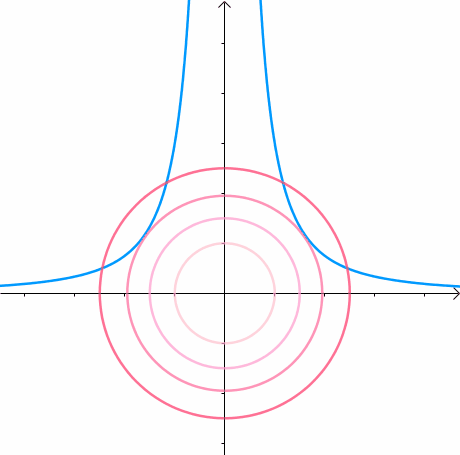
显然，第一次与 相交的点就是距离原点最近的点：

此时，圆和曲线相切，也就是在该点切线相同：

至此，我们分析出了：2 等高线为了继续解题，需要引入等高线。这些同心圆：

可以看作函数 的等高线：

根据梯度的性质（关于梯度可以查看如何通俗地理解梯度？），梯度向量：是等高线的法线：
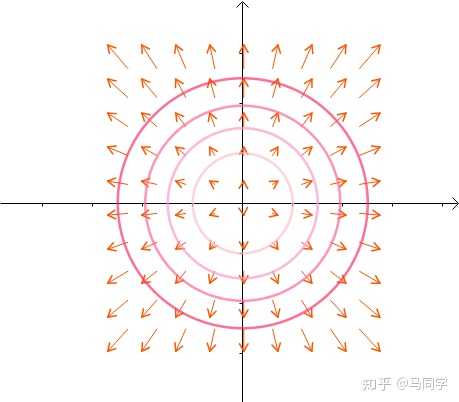另外一个函数 的等高线为：
之前的曲线 就是其中值为3的等高线：

因此，梯度向量：也垂直于等高线 ：

梯度向量是等高线的法线，更准确地表述是：3 拉格朗日乘子法3.1 求解根据之前的两个分析：综合可知，在相切点，圆的梯度向量和曲线的梯度向量平行：

也就是梯度向量平行，用数学符号表示为：还必须引入 这个条件，否则这么多等高线，不知道指的是哪一根：

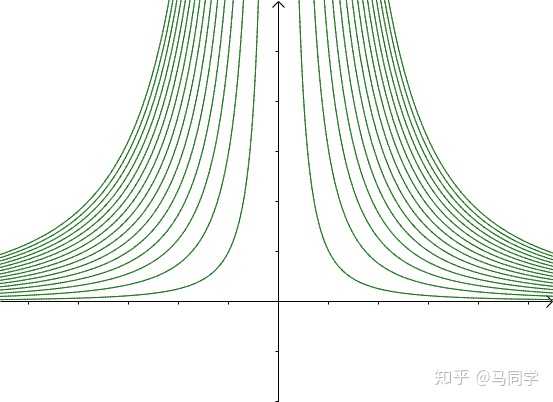
因此联立方程：求一下试试：这就是拉格朗日乘子法。3.2 定义要求函数 在 约束下的极值这种问题可以表示为： 意思是subject to，服从于，约束于的意思。可以列出方程组进行求解：用这个定义来翻译下刚才的例子，要求：令：求：联立方程进行求解：3.3 变形这个定义还有种变形也比较常见，要求：定义：求解下面方程组即可得到答案：把等式左边的偏导算出来就和上面的定义是一样的了。3.4 多个约束条件如果增加一个约束条件呢？比如说：求：从图上看约束条件是这样的：

很显然所求的距离是这样的：

那这三者的法线又有什么关系呢？ 的法线是 和 的法线的线性组合：

假设：那么线性组合就表示为：联立方程：即可求解。往更高纬度走的话，多约束条件的情况下，问题变为了 围成的曲线 和 相切，直观上看 必然在 张成的空间中：

这点的严格性这里就不证明了。文章最新版本在（有可能会有后续更新）：如何理解拉格朗日乘子法？编辑于 2018-07-31予人玫瑰，手有余香赞赏8 人已赞赏​已赞同 1505​​64 条评论​分享​收藏​喜欢​收起​lemonvisual state estimation256 人赞同了该回答为什么出现拉格朗日乘子法？最短路径问题从几何意义中获得灵感：从数学公式中获得灵感推广到高维空间------------------------------------------------------一个最短路径问题

假设你在M点，需要先到河边（上图右侧曲线 ）再回到C点，如何规划路线最短？假设： 河流曲线满足方程 g(x,y) = 0 （例如 如果它是一个圆： ）用P表示河边上的任意P(x,y)点，用d(M,P)表示M,P之间距离，那么问题可以描述为： , 约束于 如何求解问题？ 1. 从几何意义中获得灵感：首先，f§是一个标量（只有大小没有方向），那么在上图的二维空间中必然存在了一个标量场f§，即对于每一个点P都对应着一个f§值，它代表经过该点的路径总和是多少。如果我们画出它的等值线（场线)，就会发现它呈椭圆向外辐射：

显然，f§的等值线与河边曲线的交点P即为我们想求的点。那么问题来了: 这样的点满足何种性质？ （如果没有性质也就无法列出关系式进行求解，但是这么特殊的点极有可能存在良好某种特性）最直观的性质： 等值线（椭圆）在P点的法向量n与河边曲线的法向量m平行：

而在多元微积分中，一个函数h在某一点P的梯度是点P所在等值线（二维）或等值面（三维）的法向量，即，所以对于函数 f , g ： （注意 梯度是一个向量，准备在另一个问题中对梯度的概念做详细阐述）即由相交点的性质我们得到了2个关系式（因为是二维平面，对于三维则可以得到三个关系式，以此类推），再加上我们的约束条件：一共3个关系式，由线性代数中知识可知 3个关系式，3个未知量（）极有可能有唯一解，当然也不排除会出现多个解甚至无穷多解 （例如 下图 河边是一条直线，且M,C就在河边时）。(关于这个知识点稍后在其它答案中给出解释)。

2. 从数学公式中获得灵感仍人是问题： 我们知道在多元微积分中如果想求一个函数的极值一般的做法是把 ，如何把这个公式和我们的约束条件 统一在一起呢？答案是： 引入 并且定义一个新的函数： ，令： 与我们要求解的优化问题是 等价的： 因为: 与约束条件等价，而且此时 即拉格朗日函数与我们的目标函数 取相同值。 用拉格朗日函数把目标函数和约束条件统一在了一起。 实际上这种方法与上面的几何方法是完全等价的：
3. 3. 推广到高维空间以上我们一直在讨论 二维的情形，下面让我们看看这个问题的高维情况： 以几何观点为例：假设约束条件变成 ，其中 h是紫色椭球面， g是平面。它们相交于黑色的环，且在相交线上（黑色环）各自的方向向量（） 与相交线垂直。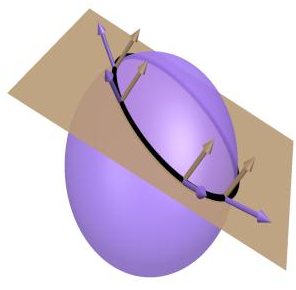对于我们的目标函数 ，下图中红色椭球是它的等值面。它与黑色环的交点 ，此处的向量
4. 更高维度同理。
主要内容转载自知乎如何理解拉格朗日乘子法？ - 马同学的回答 - 知乎
https://www.zhihu.com/question/38586401/answer/457058079
其他参考：
https://www.cnblogs.com/mo-wang/p/4775548.html
用于个人学习记录，侵删