[Algorithm][回溯][有效的数独][解数独]详细讲解-CSDN博客

本文链接：https://blog.csdn.net/qq_37281656/article/details/138978779

1.有效的数独

1.题目链接

有效的数独

2.算法原理详解

本题理应算是一道哈希应用的一道题，但是可作为解数独的剪枝条件
本题可以学习哈希表的使用，并且在一个二维数组中，哈希表对对应值的映射方法
如何判断一行/一列是否出现过某个数？
- bool row[9][9] -> 共9行，每行9个数是否出现过
- bool col[9][9] -> 共9列，每列9个数是否出现过
如何判断每个小九宫格是否出现过某个数
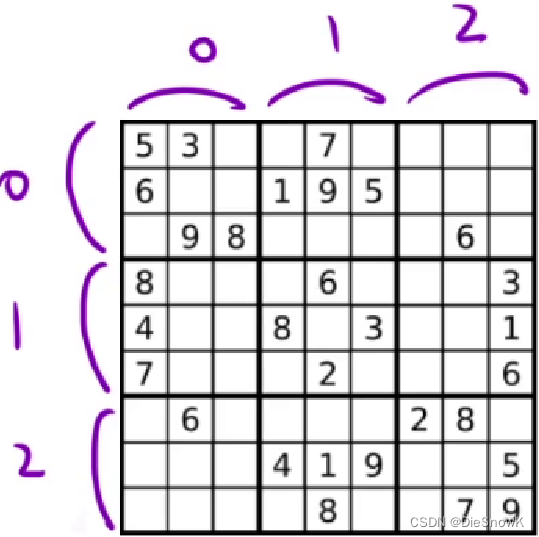
- bool grid[3][3][9] -> 每个九宫格三行三列，9个数是否出现过
- 此设计比较巧妙，row / 3 && col / 3就是对应每一"大行"特定九宫格内的对应下标
实际改如何操作呢？
- 穷举每个元素，执行上述判断即可

3.代码实现

bool isValidSudoku(vector<vector<char>>& board) 
{
    bool row[9][9] = {false};
    bool col[9][9] = {false};
    bool grid[3][3][9] = {false};

    for(int i = 0; i < 9; i++)
    {
        for(int j = 0; j < 9; j++)
        {
            if(board[i][j] != '.')
            {
                int num = board[i][j] - 1 - '0';
                if(row[i][num] || col[j][num] || grid[i / 3][j / 3][num])
                {
                    return false;
                }

                row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
            }

        }
    }

    return true;
}

2.解数独

1.题目链接

解数独

2.算法原理详解

本题函数设计，特别是返回值很值得推敲
思路：遍历棋盘每个格子，尝试填入1~9，判断是否合法
- 需要返回值来判断，是否陷入了一种无解的情况，此时return false
- 若已经无数字可填，则说明获得了最终解，此时return true
- 若某种情况下，其递归树下已经获得了最终解，那么一路返回上来，DFS(board) == true，此时无需再向后遍历了，直接return true即可
剪枝：
- 如何判断一行/一列是否出现过某个数？
  - bool row[9][9] -> 共9行，每行9个数是否出现过
  - bool col[9][9] -> 共9列，每列9个数是否出现过
- 如何判断每个小九宫格是否出现过某个数
  - bool grid[3][3][9] -> 每个九宫格三行三列，9个数是否出现过
  - 此设计比较巧妙，row / 3 && col / 3就是对应每一"大行"特定九宫格内的对应下标
- 实际改如何操作呢？
  - 穷举每个元素，执行上述判断即可

3.代码实现

class Solution 
{
    bool row[9][10] = {false};
    bool col[9][10] = {false};
    bool grid[3][3][10] = {false};
public:
    void solveSudoku(vector<vector<char>>& board) 
    {
        // Init
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] != '.')
                {
                    int num = board[i][j] - '0'; // 下标映射
                    row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                }
            }
        }
        
        DFS(board);
    }
    
    bool DFS(vector<vector<char>>& board)
    {
        for(int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                if(board[i][j] == '.') // 此处无数字
                {
                    for(int num = 1; num <= 9; num++) // 枚举每一个数字
                    {
                        if(!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num]) // 合法性检验
                        {
                            board[i][j] = num + '0';
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = true;
                        
                            if(DFS(board) == true)
                            {
                                // 当得到最终解后，就没必要往后枚举了
                                return true; // 重点理解
                            }
                        
                            // 若没有最终解，说明上述情况不行，需要回溯
                            board[i][j] = '.';
                            row[i][num] = col[j][num] = grid[i / 3][j / 3][num] = false;
                        }
                    }
                    
                    // 当全部数字都尝试无果后，标识这种情况无解
                    return false; // 重点理解
                }
            }
        }
        
        // 无数字可填，表明解出最终解
        return true; // 重点理解
    }
};