UVALive3126[Taxi Cab Scheme] DAG最小路径覆盖模型

DAG最小路径覆盖模型

---

1.最小路径覆盖是什么？

最小路径覆盖，就是在图中找尽量少的路径，使得每个结点恰好在一条路径上。

换句话说就是，任意两条路径没有公共点。

2.如何求最小路径覆盖？

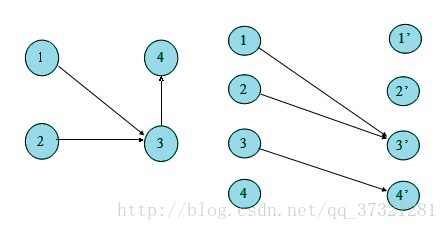
我们可以发现： 在DAG中，每条路径除了结尾的点，其他每个点都有一个唯一的后继结点。

举个例子：上图中 2->3->4 这条路径上， 2的后继3、3的后继是4、4没有后继。

---

那么求 路径条数 的问题可以转换为求 结尾结点 的个数。

1.我们把DAG中的每个点 u 拆分成两个点 u 和 u’把 u放入二分图的X集合，u’放入Y集合。

2如果u->v有一条边，那么在二分图中连接u->v’ .

上面左图 ，按照以上两个步骤 ，可以建出右图。

因为每个点只属于一条路径，我们可以想到二分图匹配。

因为DAG中每个点的后继结点 就是 它在二分图上的匹配点

所以 二分图最大匹配数=DAG中有后继结点的点的个数。

我们要求 结尾结点（没有后继结点的点）的个数， 那么

最小路径数=结尾结点数=n-非结尾结点数=n-最大匹配数。 所以，

最小路径覆盖数=结点数-最大匹配数

---

题目链接

---

题目大意：现在有n个客户，他们要乘出租车，他们每个人，有一个出发时间t，起点位置和终点位置。现在要安排尽量少的出租车送他们到目的地。出租车必须在客户出发前至少提前一分钟赶到那个客户出发的位置才行，或者这个客户就是这辆出租车的第一个乘客。让你输出需要的最少的出租车数。

---

solution：如果客户u和客户v能用一辆出租车搞定，那么就连一条边。然后跑匈牙利算法。

#include <vector>
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 505;

vector<int> G[N];

int line[N], n;
bool S[N], T[N];

bool find(int x){
    S[x]=true;
    for ( int i=0; i<G[x].size(); i++ ){
        int v=G[x][i];
        if( !T[v] ){
            T[v]=1;
            if( line[v]==0 || find( line[v] ) ){
                line[v]=x;
                return true;
            } 
        }
    }
    return false;
}

int HUN(){
    int ans=0;
    memset(line,0,sizeof(line));
    for ( int i=1; i<=n; i++ ){
        memset(S,0,sizeof(S));
        memset(T,0,sizeof(T));
        if( find(i) ) ans++;
    }
    return n-ans;
}

struct Point{
    int t, tE;
    int xS, yS, xE, yE;
}P[N];

int get_t( Point x, Point y ){
    return abs( y.yE-x.yS ) + abs( y.xE-x.xS );
}
int get_tP( Point x ){
    return abs( x.yE-x.yS ) + abs( x.xE-x.xS );
}
int readin(){
    int x=0; char ch=getchar();
    while( !isdigit(ch) ) {
        ch=getchar();
    }
    while( isdigit(ch) ) {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x;
}

int main(){
    int tt=readin();
    while( tt-- ){
        scanf("%d", &n);
        for ( int i=1; i<=n; i++ ) G[i].clear();
        for ( int i=1; i<=n; i++ ) {
            int t1=readin();
            P[i].t=readin()+t1*60;
            P[i].xS=readin(), P[i].yS=readin(), P[i].xE=readin(), P[i].yE=readin();
            P[i].tE=P[i].t+get_tP( P[i] );
        }
        for ( int i=1; i<=n; i++ )
            for ( int j=1; j<=n; j++ )
                if( i!=j && P[j].t-P[i].tE > get_t( P[j], P[i] ) ) G[i].push_back(j);
        printf("%d\n", HUN() );
    }
}