1.推荐系统概览
1.1 推荐系统是互联网的增长引擎
-
互联网企业的核心需求是“增长”,而推荐系统正处在增长引擎的核心位置。
-
推荐系统要解决的用户痛点是用户如何在信息过载的情况下高效的获得感兴趣的信息。
1.2 推荐系统的架构
-
数据部分 客户端及服务端实时数据处理 ——> 流处理平台准实时数据处理 ——> 大数据平台离线数据处理 场景信息 - 物品信息 - 用户信息 ——> 特诊工程 ——> 用户特征 - 物品特征 - 场景特征
-
模型部分 候选物品库 ——> 召回层 -》排序层 -》补充策略与算法层 ——> 物品推荐列表 模型离线训练(离线测试) — 模型在线更新(线上A/B测试)
图片引用自 GitHub项目:https://github.com/wzhe06/SparrowRecSys

2.传统推荐学习算法
2.1 传统推荐模型的演化关系图

2.2.协同过滤算法族(CF - collaborative filtering)
1.协同过滤
1)相似性度量
-
余弦相似度
-
皮尔逊相关系数(减去均值的余弦相似度,减去用户均值、物品均值)
2)评分预测
-
userCF 适用于兴趣变化场景、社交性强的场景
相似度作为权重,加权其他用户对于该物品的评分
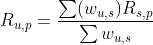
-
itemCF
适用于兴趣稳定场景
选取目标用户的正反馈物品 寻找相似物品,基于相似度排序推荐
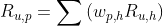
3)缺点、限制(userCF)
-
用户数目大于物品数目
-
指数增长的相似度矩阵大小
-
用户历史数据稀疏
-
处理稀疏向量能力差,容易出现头部效应
-
无法引入其他信息:用户年龄、商品描述等
2.矩阵分解
1) 分解隐含向量维度k,取值越大表达能力强,泛化能力弱。
2) 分解方法:
-
奇异值分解 缺点:要求原始矩阵稠密;分解复杂度达到
-
特征值分解
-
梯度下降法 消除用户和物品打分偏差
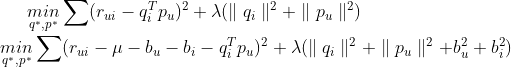
3) 优缺点
-
不方便加入其他特征
-
泛化能力强
-
算法复杂度低
-
隐含变量方便特征拼接
2.3 逻辑回归模型族(LR - logistic regression)
1)转化为点击率(CTR - click through rate)预测问题
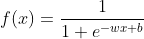
2) 优缺点
-
无法进行特征交叉,特征筛选
-
辛普森悖论:在特征组合分组中占优势的一方,在但特征汇总情况下可能变成劣势一方。
2.4 因子分解机模型族(FM - factorization machine)
1.POLY2模型
无差别进行特征组合
参数量:nn
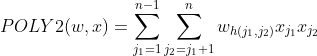
优缺点:
-
特征矩阵更加稀疏
-
参数量从n变为
2.FM模型 —— 隐向量特征交叉
从单纯的用户物品隐向量 ——> 所有特征隐向量,为每个特征构建一个隐向量
参数量:nk
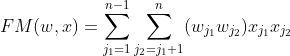
优缺点:
-
大幅降低对于数据稀疏性要求
3.FFM模型 ——特征域
引入特征域,参数量变为:nkf —> knn
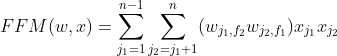
2.5 组合模型
1.GBDT + LR
利用GBDT自动进行特征筛选和组合,生成新的特征向量。
通过LR进行CTR任务。
优缺点:
-
决策树的深度决定特征交叉阶数
-
GBDT容易产生过拟合,丢失了大量的数值特征
2.LS-PLM (large scale piece-wise linear model)
又被称为MLR (mixed logistic regression)
阿里巴巴曾经主流的推荐模型。
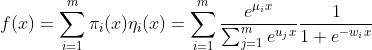
1)主要思想
先聚类在LR预测
2)优缺点
-
端到端的非线性学习能力,分片能力,挖掘数据中蕴含的非线性模式。
-
模型的稀疏性强








 本文介绍推荐系统,它是互联网增长引擎,可解决用户信息过载问题。阐述其架构,包括数据和模型部分。还介绍传统推荐学习算法,如协同过滤算法族、逻辑回归模型族、因子分解机模型族及组合模型,分析各算法优缺点。
本文介绍推荐系统,它是互联网增长引擎,可解决用户信息过载问题。阐述其架构,包括数据和模型部分。还介绍传统推荐学习算法,如协同过滤算法族、逻辑回归模型族、因子分解机模型族及组合模型,分析各算法优缺点。
















 8025
8025

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








