毕业设计：基于WEB的RSA加密算法优化系统

目录

前言

课题背景和意义

实现技术思路

一、算法理论技术

1.1 RSA 加密算法

1.2 多素数 RSA 加密算法

1.3 参数替换

二、实验及结果分析

最后

---

前言

    📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。

🚀对毕设有任何疑问都可以问学长哦!

    选题指导:

        最新最全计算机专业毕设选题精选推荐汇总

        大家好,这里是海浪学长毕设专题,本次分享的课题是

       🎯基于WEB的RSA加密算法优化系统

课题背景和意义

       随着网络技术的飞速发展，信息安全问题日益凸显，加密算法作为保障信息安全的重要手段之一，受到了广泛关注。RSA加密算法作为公钥加密算法的代表，被广泛应用于数据加密和数字签名等领域。然而，传统的RSA加密算法在实现效率和安全性方面仍存在一定的不足，亟待优化。基于WEB的RSA加密算法优化系统的研究，旨在通过改进算法实现方式、提高加密解密效率、增强系统安全性，以满足日益增长的信息安全需求。这一课题的研究不仅具有重要的理论价值，还有助于推动加密算法在实际应用中的发展和完善。

实现技术思路

一、算法理论技术

1.1 RSA 加密算法

       RSA公钥密码体制基于大素数和模幂算法。它安全、易于实现，广泛用于数据加密、数字签名和证书制作。尽管应用广泛，但密钥生成和加解密操作的耗时问题制约了其更广泛应用。RSA包括密钥生成、加密和解密三个阶段：选择大素数生成模数和公私钥，用公钥加密消息为密文，再用私钥从密文解密出原消息。

       RSA加密解密全过程如下：

       密钥生成阶段：

• 选择两个不相等的质数p和q，计算它们的乘积n=p*q，n将作为公钥和私钥的一部分。
• 计算n的欧拉函数φ(n)=(p-1)*(q-1)。
• 选择一个小于φ(n)且与φ(n)互质的整数e作为公钥的一部分，e通常选择65537。
• 计算e对于φ(n)的模反元素d，即满足e*d mod φ(n) = 1的整数d，d将作为私钥的一部分。
• 公钥为(e, n)，私钥为(d, n)。销毁p、q和φ(n)的记录，只保留公钥和私钥。

        加密阶段：

• 假设要加密的明文消息为M，首先将M转换为一个小于n的非负整数m。这可以通过将明文消息的每个字符转换为对应的ASCII码，然后将这些ASCII码连接在一起实现。
• 使用公钥(e, n)对m进行加密，加密公式为C = m^e mod n，其中C为加密后的密文。
• 将密文C发送给接收方。

       解密阶段：

• 接收方收到密文C后，使用私钥(d, n)对C进行解密，解密公式为m = C^d mod n，其中m为解密后的明文对应的整数。
• 将m转换回原始的明文消息M。这可以通过将m的每一段对应回ASCII码，然后将这些ASCII码转换回字符实现。

 相关代码示例：

import rsa  
  
# 密钥生成阶段  
(public_key, private_key) = rsa.newkeys(512)  # 生成512位的RSA密钥对  
  
# 将密钥对转换为可用于加密解密的格式  
pub_key_pem = public_key.save_pkcs1('PEM')  
priv_key_pem = private_key.save_pkcs1('PEM')  
  
# 加载密钥对  
public_key_loaded = rsa.PublicKey.load_pkcs1(pub_key_pem)  
private_key_loaded = rsa.PrivateKey.load_pkcs1(priv_key_pem)  
  
# 加密阶段  
message = 'Hello, RSA!'.encode('utf8')  # 明文消息  
crypto_message = rsa.encrypt(message, public_key_loaded)  # 加密  
  
# 解密阶段  
decrypted_message = rsa.decrypt(crypto_message, private_key_loaded)  # 解密  
decrypted_message = decrypted_message.decode('utf8')  # 将解密后的字节串解码为字符串  
  
# 输出结果  
print('Original message:', message)  
print('Encrypted message:', crypto_message)  
print('Decrypted message:', decrypted_message)  
  
# 验证解密后的消息是否与原始消息相同  
assert message == decrypted_message.encode('utf8'), 'Decryption failed!'  
print('Decryption successful!')

1.2 多素数 RSA 加密算法

       多素数RSA加密算法是RSA的一个变种，它使用多个强素数来生成密钥，从而增加了算法的安全性。在密钥生成阶段，选择多个不同的强素数并计算它们的乘积作为模数，再计算模数的欧拉函数。公钥是一个小于欧拉函数且与欧拉函数互质的正整数，而私钥则是公钥关于欧拉函数的模逆元素。加密时，使用公钥对明文消息进行加密得到密文消息。解密时，使用私钥对密文消息进行解密得到明文消息。这种方法通过增加素数的数量和复杂度来提高RSA算法的安全性，但也需要更多的计算资源和时间来处理。

       强素数快速生成算法通过结合随机大数生成与概率素数测试来产生强素数。算法首先构造特定格式的大数，随后根据数值大小选择试除法或Miller-Rabin素性检测来验证其素性，从而在保证速度的同时提高了素数检测的准确性。经Miller-Rabin测试通过的数在很大概率上可被视为素数。

相关代码示例：

def generate_random_large_number(bits=256):  
    random_bytes = random.getrandbits(bits - 2).to_bytes((bits + 7) // 8, 'big')  
    random_bytes = (1 << ((bits - 1) % 8)) | random_bytes  
    if bits % 8 == 0:  
        random_bytes |= 1  
    return int.from_bytes(random_bytes, 'big')  
  
def generate_strong_prime(bits=256, k=5, attempts=100):  
    """  
    尝试生成指定位数的强素数  
    attempts指定最大尝试次数  
    """  
    for _ in range(attempts):  
        p = generate_random_large_number(bits)  
        if miller_rabin(p, k):  
            return p  
    raise ValueError("Unable to find a strong prime within the specified attempts.")  

1.3 参数替换

       在多素数RSA加密算法的基础上，通过引入全新参数𝑥代替原算法中的模数𝑁，提高了算法的安全性。新参数的计算依赖于所选的多个强素数，确保𝑥与𝑁之间存在特定的数学关系，从而使攻击者难以通过因式分解攻击获取私钥。在加密和解密过程中，使用新参数𝑥代替模数𝑁进行操作，保证了算法的正确性和安全性。这种优化方法增加了算法的复杂性和破解难度，提高了RSA加密算法的整体安全性。

二、实验及结果分析

       获取私钥d的时间取决于多个因素，包括所使用的加密算法、密钥长度、计算能力以及攻击方法等。私钥d是通过公钥加密算法生成的，其生成时间取决于算法的复杂性和计算能力。然而，一旦私钥d生成，获取它的时间将取决于如何存储和保护它。对于合法的密钥持有者或使用者来说，他们通常会有安全的方式来存储和访问私钥d，而不需要进行破解。

       基于多重密钥的RSA加密算法相较于传统RSA算法，在素数长度较小时提升获取私钥时间的效果较缓慢，但随着素数长度的增加，其提升效果愈发显著。该算法通过使用不同的密钥对明文消息进行加密，有效避免了公共模数攻击，并确保了整体明文消息不再单一依赖于同一个公钥，从而显著增强了算法的安全性。

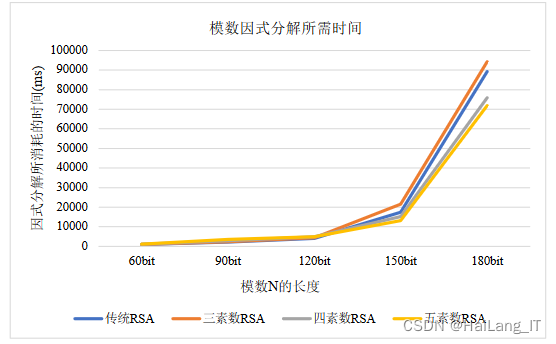
 相关代码示例：

def mod_inverse(a, m):  
    for x in range(1, m):  
        if (a * x) % m == 1:  
            return x  
    return None  
  
# RSA密钥生成函数  
def generate_keypair(p, q):  
    n = p * q  
    phi = (p - 1) * (q - 1)  
  
    # 选择一个e，使得1 < e < phi，且gcd(e, phi) = 1  
    e = random.randrange(1, phi)  
    while gcd(e, phi) != 1:  
        e = random.randrange(1, phi)  
  
    # 计算d，使得d是e关于phi的模逆元  
    d = mod_inverse(e, phi)  
    return ((e, n), (d, n))  # 返回公钥和私钥  
  
# RSA加密函数  
def encrypt(pk, plaintext):  
    e, n = pk  
    ciphertext = [pow(ord(char), e, n) for char in plaintext]  
    return ciphertext  

实现效果图样例：

最后

我是海浪学长,创作不易,欢迎点赞、关注、收藏。

毕设帮助，疑难解答，欢迎打扰！