acm用到的数学公式记录

最新推荐文章于 2024-05-20 15:27:11 发布

qq_37383726

最新推荐文章于 2024-05-20 15:27:11 发布

阅读量1.8k

点赞数 9

分类专栏：结构的模版

本文链接：https://blog.csdn.net/qq_37383726/article/details/76532157

版权

结构的模版专栏收录该内容

101 篇文章 0 订阅

订阅专栏

& o(n)筛出n以内数字的质因子个数。

Vis[0] = Vis[1] = true;
    for(int i = 2; i < MAXN; i++) {
        if(!Vis[i]) {
            Primefactor[i] = 1;
            for(int j = 2 * i; j < MAXN; j += i) {
                Vis[j] = true;
                Primefactor[j]++;
            }
        }
    }

& 求一个区间所有数的所有因子的和（包括自身和1）

LL sum[MAXN],sum[MAXN];
void dabiao(){// 打表因子和
    for(int i=2;i*i<=MAXN;i++){
        for(int j=i;i*j<=MAXN;j++){
            if(i!=j)  ans[j*i]+=i+j;
            else ans[j*i]+=i;
        }
    }
    sum[1]=1;//这里打表啦前缀和 来求区间的
    for(int i=2;i<=MAXN;i++)
        sum[i]=sum[i-1]+ans[i]+i+1;// 要加上 自身 和 1
}

& 欧拉筛筛出每个数的最小非1因子

int mifac[maxn];bool prime[maxn]={0};
void init(){
    for(int i=2;i<maxn;i++)  mifac[i]=i;
    for(int i=2;i<maxn;i++){
        if(prime[i]==0){
            for(int j=2;i*j<maxn;j++){
                mifac[i*j]=min(mifac[i*j],i);
                prime[i*j]=1;
            }
        }
    }   
}


bool su[MAXN + 1];
int mu[MAXN + 1], phi[MAXN + 1], prm[MAXN + 1], cnt;
inline void euler()
{
    su[0] = su[1] = true;
    mu[1] = 1;
    phi[1] = 1;
    for (int i = 2; i <= MAXN; i++) {
        if (!su[i]) {
            prm[++cnt] = i;
            mu[i] = -1;
            phi[i] = i - 1;
        }
        for (int j = 1; j <= cnt; j++) {
            int t = i * prm[j];
            if (t > MAXN) break;
            su[t] = true;
            if (i % prm[j] == 0) {
                mu[t] = 0;
                phi[t] = phi[i] * prm[j];
                break;
            } else {
                mu[t] = -mu[i];
                phi[t] = phi[i] * (prm[j] - 1);
            }
        }
    }
}

< 1 > 欧拉函数的求解
欧拉函数定义
这里写图片描述

性质
1 一个素数的比它小的互质数的个数为该数减一，ψ(P)=P-1。
2 假如ψ(N)的欧拉函数值为p，则N的最小值为大于p的最小素数。
两种

 LL eular(LL n){ //单独求欧拉函数值
    LL ans=n;
    for(LL i=2;i*i<=n;i++){
        if(n%i==0){
            ans=ans/i*(i-1); 
            while(n%i==0)   n/=i;
        }
    }
    if(n>1) ans=ans/n*(n-1);
    return ans;
}

LL e[MAXN];//欧拉筛法
void eular(){
    for(int i=0;i<MAXN;i++) e[i]=i;
    for(int i=2;i<MAXN;i++)
        if(e[i]==i)
            for(int j=i;j<MAXN;j+=i) e[j]=e[j]/i*(i-1);
}

&
这里写图片描述

bool su[MAXN]={1,1,0};//素筛
void shai(){
    for(int i=2;i*i<=MAXN;i++)
        if(!su[i])  
            for(int j=i*i;j<MAXN;j+=i) 
                su[j]=1;
}

//筛出素数
int su[MAXN], prm[MAXN],sz;
void init() {
    for(int i = 2; i < MAXN; ++i) {
        if(!su[i])  prm[sz++] = i;
        for(int j = 0; j < sz; ++j) {
            int t = i * prm[j];
            if(t >= MAXN) break;
            su[t] = true;
            if(i%prm[j] == 0) break;
        }
    }
}

& 在O(log n / log p)时间内求出n!的质因子分解中质数p的指数：(勒让德定理的简化算法）

inline int getn(int n, int p) {  //n！的质因子p的指数
    int sum = 0;  
    while (n) {   n /= p;  sum += n; }   
    return sum;  
}

&
这里写图片描述

& 逆元
知识点链接

< 2 > 容斥原理
1）求数n的质因数

LL p[30],ge;
void getn(LL n){
    ge=0;
    for(LL i=2;i*i<=n;i++){
        if(n%i==0) p[ge++]=i;
        while(n%i==0) n/=i;
    }
    if(n>1) p[ge++]=n;
}

2）求[1,n] 区间内和m互质的个数

LL p[30],ge;
void getn(LL n){
    ge=0;
    for(LL i=2;i*i<=n;i++){
        if(n%i==0) p[ge++]=i;
        while(n%i==0) n/=i;
    }
    if(n>1) p[ge++]=n;
}
int que[MAXN],top;
LL nop(LL m){
    top=0;
    que[top++]=-1;
    for(int i=0;i<ge;i++){
        int t=top;
        for(int j=0;j<t;j++)
            que[top++]=(-1)*que[j]*p[i];
    }
    LL ans=0;
    for(int i=1;i<top;i++) ans+=m/que[i];
    return m-ans;
}

3 ）求q区间[1,n]和区间[1,n] 不重复的质数对==》求[1,n]的所有数字的欧拉函数的和

4）给定个数组arr和数n，问这个数组内有多少个数与m互质。
我门我可以先求能够被整除的个数，然后一减，就是不可以整除的个数。
这里写图片描述

LL gcd(LL a,LL b) {  return b==0?a:gcd(b,a%b) ; }
LL lcm(LL a,LL b) { return a/gcd(a,b)*b ; }
LL arr[MAXN],ge;  // 容斥定理
LL que[MAXN],top;
LL nop(LL m){
    top=0;
    que[top++]=-1;
    for(int i=0;i<ge;i++){
        LL temp=top;
        for(int j=0;j<temp;j++){ // 这里也是控制了 奇加偶减。
            LL f=1;
            if(que[j]<0) f=-1;
            que[top++]=f*lcm(abs(que[j]),p[i])*(-1);
        }
    }
    LL sum=0;
    for(LL i=1;i<top;i++){
        sum+=m/que[i];
    }
    return m-sum; //sum中是能够被整除的不重复的个数
}

< 3 > 欧几里得
这里写图片描述

LL gcd(LL a,LL b) {  return b==0?a:gcd(b,a%b) ; }
LL lcm(LL a,LL b) { return a/gcd(a,b)*b ; }

扩展欧几里得
这里写图片描述

用扩展欧几里得计算最小逆元
这里写图片描述

< 4 > 矩阵
1）矩阵快速幂
常用来求递归式子的第n项
初始矩阵*过渡矩阵的k次幂==最后的结果
例题
下面代码是上述例题的代码

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int MAXN = 20;
const int MAXM = 1e6;
const int inf=0x3f3f3f3f;
LL mod,n;
struct Matrix {
    LL a[MAXN][MAXN];
    int h,w;
}ori,res,it;
LL f[20]={0,1,2,3,4,5,6,7,8,9}; //  初始函数值 

void init(){
    res.h=res.w=10;
    memset(res.a,0,sizeof(res.a));//单位矩阵，结果矩阵
    for(int i=1;i<=10;i++) res.a[i][i]=1;
    ori.h=ori.w=10;
    memset(ori.a,0,sizeof(ori.a));
    //此处输入过渡矩阵

//  puts("res ;");
//  for(int i=1;i<=10;i++) {//输出 单位矩阵
//      for(int j=1;j<=10;j++)
//      printf("%lld ",res.a[i][j]);
//      puts("");
//  }
//  puts("ori ;");
//  for(int i=1;i<=10;i++) {//输出过渡矩阵
//      for(int j=1;j<=10;j++)
//      printf("%lld ",ori.a[i][j]);
//      puts("");
//  }
//  puts("it ;");  // 输出初始矩阵
//  for(int i=1;i<=1;i++) {
//      for(int j=1;j<=10;j++)
//      printf("%lld ",it.a[i][j]);
//      puts("");
//  }
}
Matrix multi(Matrix x,Matrix y){
    Matrix z;
    z.h=x.h;z.w=y.w;memset(z.a,0,sizeof(z.a));
    for(int i=1;i<=x.h;i++){
        for(int k=1;k<=x.w;k++){
            if(x.a[i][k]==0) continue;
            for(int j=1;j<=y.w;j++){
                z.a[i][j]=(z.a[i][j]+x.a[i][k]*y.a[k][j]%mod)%mod;
            }
        }
    }
    return z;
}
void Matrix_mod(int n){
    while(n){
        if(n&1) res=multi(ori,res);
        ori=multi(ori,ori);
        n>>=1;
    }
    res=multi(it,res);//结果矩阵乘初始矩阵
    printf("%lld\n",res.a[1][1]%mod);
}
int main(){
    it.h=1;it.w=10;
    for(int i=10;i>=1;i--) it.a[1][i]=f[10-i];
    while(scanf("%lld%lld",&n,&mod)!=EOF){
        for(int i=1;i<=10;i++){
            scanf("%lld",&a[i]);
          }
        init();
        if(n<10) printf("%lld\n",f[n]%mod);// 小于的时候应该输出 初值
        else  Matrix_mod(n-9); // 否则输出快速幂求解的
    }
    return 0;
}

& 斐波那契的通项公式
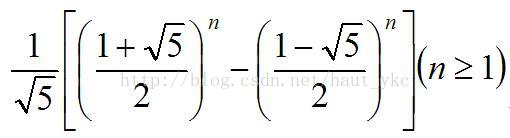
这里写图片描述
取完对数之后

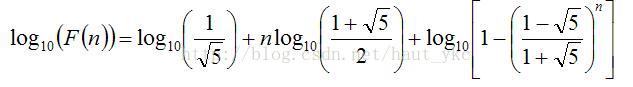
求第n项的前m位
又因为当n很大时，log10(1-((1-√5)/(1+√5))^n)->0
故原始可化为log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0); 最后取小数部分即可
代码

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int MAXN = 1e2;
const int MAXM = 1e5;
LL f[55]={0,1,1,2};
int main(){
    for(int i=4;i<27;i++) {
        f[i]=f[i-1]+f[i-2];
    //printf("i== %d   %lld\n",i,f[i]);
    }
    int n;
    while(scanf("%d",&n)!=EOF){
        if(n<=25) printf("%d\n",f[n]) ;
        else {
         double temp=-0.5*log(5.0)/log(10.0)+((double)n)*log((sqrt(5.0)+1.0)/2.0)/log(10.0);
         temp-=floor(temp);
         temp=pow(10.0,temp);
         while(temp<10000) temp*=10;  // 这里是前五位
         printf("%d\n",(int)temp);
        }
    }
    return 0;
}

& 一般的求一个数字的前n位

double x,temp;
while(scanf("%lf",&x)!=EOF)
{
temp=log(x)/log(10.0);
temp=temp-floor(temp); //floor(temp)函数求出小于temp的最大整数
temp=pow(10.0,temp);
while(temp<1000)// 此处是四位
temp*=10;
//printf("%.0lf\n",temp); //采用浮点表达法时会四舍五入
printf("%d\n",(int)temp);//此处不需四舍五入，直接舍弃后面的位
}
}

& 判断n!是否能够被m整除

&因子和的计算方法
因子和：一个数的所以因子的和就叫因子和。。。
举个例子：12的因子和为：1+2+3+4+6+12
计算方法是把12分解为质因数的表达形式2^2*3
那么他的因子和就是：(1+2+2^2)*(1+3) // 其实每一个都可以用等比数列求和公式
证明写起来比较麻烦，大体上思路就是牛顿二项式。。

&高斯公式
这里写图片描述
& 哥德巴赫猜想
一个大偶数(>=4)必然可以拆分为两个素数的和，虽然目前还没有人能够从理论上进行证明，不过我根据科学家们利用计算机运算的结果，如果有一个偶数不能进行拆分，那么这个偶数至少是一个上百位的数！！
所以在ACM的世界中（数据量往往只有2^63以下）哥德巴赫猜想是成立的！！所以拆分程序一定能够实现的
哥德巴赫猜想的推广
任意一个>=8的整数一定能够拆分为四个素数的和
先来说8=2+2+2+2，（四个最小素数的和）不能再找到比2小的素数了，所以当n小于8，就一定不可能拆分为四个素数的和！
那么当n大于等于8，可以分情况讨论：
（1）n&1==0(n为偶数)，那么n就一定可以拆分为两个偶数的和
那么根据哥德巴赫猜想，偶数可以拆分为两个素数的和，于是，n一定可以拆分为四个素数的和
（2）n&1==1(n为奇数)，n一定可以拆分为两个偶数+1
由于有一个素数又是偶数，2，那么奇数一定有如下拆分：2+3+素数+素数

& 抽屉原理
如果现在有3个苹果，放进2个抽屉，那么至少有一个抽屉里面会有两个苹果
抽屉原理的运用扩展
现在假设有一个正整数序列a1,a2,a3,a4…..an，试证明我们一定能够找到一段连续的序列和，让这个和是n的倍数，该命题的证明就用到了抽屉原理
先构造一个序列si=a1+a2+…ai
然后分别对于si取模，如果其中有一个sk%n==0，那么a1+a2+…+ak就一定是n的倍数（该种情况得证）
下面是上一种情况的反面，即任何一个sk对于n的余数都不为0
对于这种情况，我们可以如下考虑，因为si%n!=0
那么si%n的范围必然在1——（n-1），所以原序列si就产生了n个范围在1——（n-1）的余数，于是抽屉原理就来了，n个数放进n-1个盒子里面，必然至少有两个余数会重复，那么这两个sk1,sk2之差必然是n的倍数，
而sk1-sk2是一段连续的序列，那么原命题就得到了证明了

& 立方和公式
这里写图片描述
计算结果如下： 1³+2³+3³+…+n³=（n*(n+1)/2）²

& 求约数的个数
例题

& 求一个定积分的值
例题
Simpson`s 3/8 rule

 double a1,b1;
inline double f(double x){  // 被积函数，据题而定
    return a1*x+b1;
}

inline double getappr(double a,double b){
    return (b-a)*(f(a)+f(b)+3*f((2*a+b)/3)+3*f((a+2*b)/3))/8.0;
 } 
double simpson(double l,double r) { // 近似计算 积分
    double sum=getappr(l,r);
    double mid=(l+r)/2;
    double suml=getappr(l,mid);
    double sumr=getappr(mid,r);
    return fabs(sum-suml-sumr)<eps?sum:simpson(l,mid)+simpson(mid,r);
 }

& n！的末尾有几个0

int f(int n) {// n！末尾有几个0
    int ans=0;
    while(n){
        ans+=n/5;
        n/=5;
    }
    printf("%d\n",ans);
}

& 进制转换

int main(){
    int n;int r; //  n转r进制  
    while(scanf("%d%d",&n,&r)!=EOF){
        int f=1; if(n<0) f=-1;  n=abs(n);
        string s="";
        while(n){
            int k=n%r;
            if(k<10) s+=k+'0';
            else s+=k+'A'-10;
            n/=r;
         }
        if(f==-1)putchar('-') ;
        reverse(s.begin(),s.end());
         cout<<s<<endl;
     }
    return 0;
}

& 将分数a/b化为小数后，小数点后第n位的数字是多少？
输入 a b n 输出第n位数字
公式 (a*10^(n-1)%b)*10/b 优先级从左到右依次
代码

LL power(LL a,LL b,LL c)
{
    LL s=1,base=a;
    while(b)
    {
        if(b&1) s=s*base%c;
        base=base*base%c;
        b>>=1;
    }
    return s%c;
}
int main()
{
    LL a,b,n;//a/b小数点后第n位
    while(~scanf("%lld%lld%lld",&a,&b,&n))
    {
        LL c=((a%b)*(power(10,n-1,b)))%b;
        printf("%lld\n",c*10/b);
     }
    return 0;
}

& 把一个正整数n拆分成若干个正整数的和，请求出这些数乘积的最大值。
根据指数函数可以知道相同的数字越多越好，所以只能是 2 和 3 的加减，
另外 2*2*2<3*3
代码

LL power(LL a,LL b,LL c){
    LL s=1,base=a%c;
    while(b){
        if(b&1) s=s*base%c;
        base=base*base%c;
        b>>=1;
    }
    return s;
}
int main(){
        LL  n;
        scanf("%lld",&n);
        if(n<4) printf("%lld\n",n);
        else{
            if(n%3==0) printf("%lld\n",power(3,n/3,mod));
            else if(n%3==1) printf("%lld\n",(4*power(3,n/3-1,mod))%mod); //多余的一个1和去掉的一个3组合成2*2=4；
            else if(n%3==2) printf("%lld\n",(2*power(3,n/3,mod))%mod);//
        }
    return 0;
}

& 判断组合数C(n,m)的奇偶性：当n&m==m为奇数，反之就是偶数

& n的k进制数的位数是多少

double a[M];
void dabiao(){//n的k进制数的位数是多少
    double d=0; a[0]=0.0;
    for(int i=1;i<M;i++) { d+=log(i); a[i]=d; }
}
int main(){   
    dabiao(); int n,m;
    scanf("%d%d",&n,&m); 
    printf("%d\n",int(a[n]/log(m))+1);
    return 0;
}

& n！有多少位
这里写图片描述

         LL n;
        scanf("%lld",&n);
        LL sum=1+0.5*log10(2*pi*n)+n*log10(n/e);//  阶乘近似公式 
        printf("%lld\n",sum);

& 求逆序对归并排序【有元素重复也可以用】

int a[MAXN],temp[MAXN];
LL ans=0;
int n;
void merge(int le,int mid,int ri){
    int i,j,k;
    i=le;j=mid+1;k=le;
    for(;i<=mid&&j<=ri;){
        if(a[i]>a[j]){
            temp[k++]=a[j++];
            ans+=mid-i+1;
        }else  temp[k++]=a[i++];
    }
    while(i<=mid) temp[k++]=a[i++];
    while(j<=ri) temp[k++]=a[j++];
    for(i=le;i<=ri;i++) a[i]=temp[i];
}
void merge_sort(int le,int ri){
    if(le<ri){
        int  mid=(le+ri)>>1;
        merge_sort(le,mid);
        merge_sort(mid+1,ri);
        merge(le,mid,ri);
    }
}
int main(){
    while(~scanf("%d",&n)){
        for(int i=0;i<n;i++) scanf("%d",&a[i]);
        ans=0;
        merge_sort(0,n-1);
        printf("%lld\n",ans);
    }
    return 0;
}

qq_37383726

关注

9
点赞
踩
19

收藏

觉得还不错? 一键收藏
1
评论
acm用到的数学公式记录

bool su[MAXN + 1];int mu[MAXN + 1], phi[MAXN + 1], prm[MAXN + 1], cnt;inline void euler(){ su[0] = su[1] = true; mu[1] = 1; phi[1] = 1; for (int i = 2; i <= MAXN; i++) { if (
复制链接

扫一扫

专栏目录