编译原理之如何绘制NFA状态图

NFA状态图设计到很多的空串驱动，无论是刚开始学还是一段时间没看，都会搞不清楚，以此文作为记录

NFA其实核心就是三种状态

r=s|t

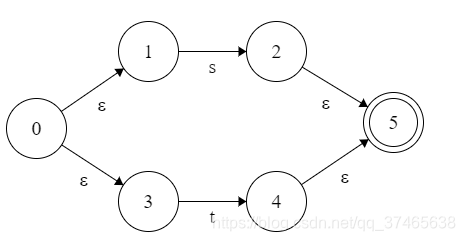
r=st

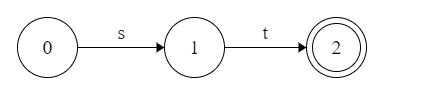
r=s*

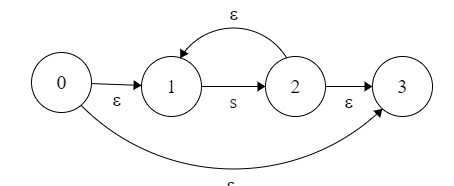
方法

其余的所有表达式都是以上三种的集合，所以我们要做的，是两点

1、记清楚三种表达式

2、区别清楚搭配的时候哪个状态和哪个状态是一致的

我们来看例子

r=(s|t)*
这显然是其中两种的组合，括号优先，我们先画括号里面,同时也分析外面

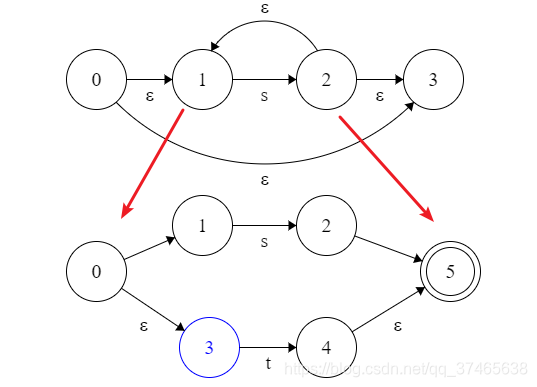
可以发现，下面的0和5作为s|t最外层的始末状态，就是(s|t)最内层的始末状态，所以两者相对应合成一个

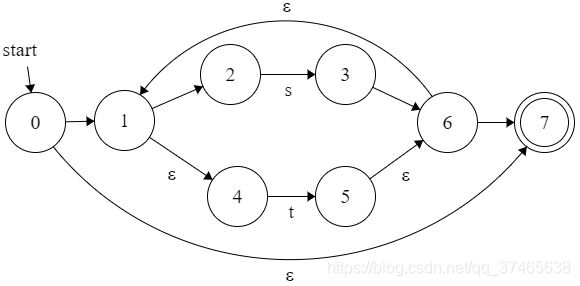
再来一个稍难的
($ϵ$|a)b*
可以看到这是 r=s|t 与r=s的合体

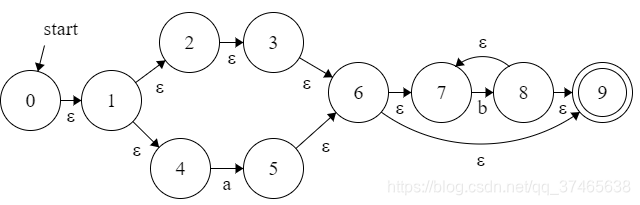
如图所示，本来1状态时初始状态，但是加了括号之后，他成为($ϵ$|a)的内部初始状态，而不是整个表达式的初始状态
同时6状态作为($ϵ$|a)的结束状态，是无缝成为b的开始状态的，因为6状态对于b来说是“其他状态的结束状态，或者是b的外部开始状态”，然后通过空串驱动而来，b的核心状态时7和8，9是“b*的外部结束状态”，所以也可作为其他状态的开始状态

总结一下 任何表达式的开始状态和结束状态都可以直接使用 r=s*的开始状态和结束状态

当然了，上式其实是可以化简的，注意到1，2，3，6之间的驱动都是$ϵ$

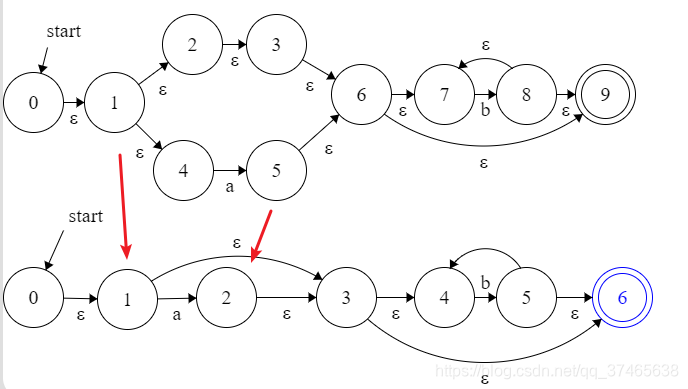
两者对比如上，由于$ϵ$直接化简，两者也不需要通过$ϵ$驱动来区分，2，4，状态也将省略

---

接下来是将NFA转换为DFA的过程，需要求出闭包
NFA的状态集对应一个DFA的状态，画表，然后绘制DFA，最后再最小化DFA的状态数量，即可画出一个DFA

这就是词法分析器的核心思想