【实验名称】基于龟壳的信息隐藏实验
值得说明的是,网上有很多龟壳算法其实现过程是不够完整的,省去了一些例如边界处理的部分。而本报告中的代码对于龟壳算法实现的是完整的,可以说是一个比较完美的复现。
【实验目的】
1、加深对图像信息隐藏基本原理和方法的掌握
2、学习并实现基于龟壳的信息隐藏和提取算法
【实验原理】
1、龟壳矩阵为一种矩阵元素有着特殊分布规律的N*N(常见如256*256)矩阵,其元素值为0-7,按照一定的差值规律连续组成。因在矩阵中值为0-7的8个元素连线形状恰如龟壳而得名
2、基于龟壳魔术矩阵的方法修改载体图像的像素来隐藏秘密信息,每个像素平均可以隐藏1.5个比特。隐藏信息后的图像用人类的肉眼很难发现和原来的载体图像有任何差异
【实验内容】
代码:
function Turtle_Shell()
clc;clear;close all;
I=imread('coverlena.bmp');
figure;subplot(1,2,1);imshow(I);
title('原图');
Secret=23; %待隐藏数据的大小
data=round(rand(1,Secret)); %随机生成大小为Secret的待隐藏的2进制数据
fprintf('隐藏数据:');disp(data);
[length,width]=size(I);
data1=zeros(1,fix(Secret/3)+1);
point=size(data1,2);
for i=Secret:-3:1
if i-3<0
num=1;
for i=i:-1:1
data1(1,point)=data1(1,point)+num*data(1,i);
num=2*num;
end
break;
end
data1(1,point)= 4*data(1,i-2)+2*data(1,i-1)+data(1,i);
point=point-1;
end
fprintf('转换成8进制:');disp(data1);
%生成龟壳矩阵
tortoise=Tortoise();
%进行信息隐藏
point=1;
for i=1:length
if point>size(data1,2)
break;
end
for j=1:2:width
if point>size(data1,2)
break;
end
%像素值0到255龟壳矩阵1到256,需将两者对齐,故此处tortoise输出时,行列+1
%输出原始信息
fprintf('待隐藏信息:%d 原像素值:%3d %3d 对应龟壳矩阵值:%d ',...
data1(point),I(i,j),I(i,j+1),tortoise(double(I(i,j))+1,double(I(i,j+1))+1));
%进行信息隐藏,即像素值修改
[I(i,j),I(i,j+1)]=find(I(i,j),I(i,j+1),data1(point),tortoise);
%输出信息隐藏后信息
fprintf('信息隐藏后像素值:%3d %3d 对应龟壳矩阵值:%d\n',...
I(i,j),I(i,j+1),tortoise(double(I(i,j))+1,double(I(i,j+1))+1));
point=point+1;
end
end
fprintf('信息隐藏成功!\r\n');
subplot(1,2,2);imshow(I);
title('隐藏后图像');
%隐藏信息读取
point=1;
for i=1:length
if point>size(data1,2)
break;
end
for j=1:2:width
if point>size(data1,2)
break;
end
%在龟壳矩阵中找出信息隐藏点,注意到像素值0到255,龟壳矩阵1到256,需将两者对齐
Data1(point)=tortoise(double(I(i,j))+1,double(I(i,j+1))+1);
point=point+1;
end
end
Data1=double(Data1);
fprintf('提取数据:');disp(Data1);
point=size(Data1,2);
for i=Secret:-3:1
if i-3<0
for i=i:-1:1
Data(1,i)=mod(Data1(1,point),2);
Data1(1,point)=(Data1(1,point)-mod(Data1(1,point),2))/2;
end
break;
end
Data(1,i)=mod(Data1(1,point),2);
Data1(1,point)=(Data1(1,point)-mod(Data1(1,point),2))/2;
Data(1,i-1)=mod(Data1(1,point),2);
Data1(1,point)=(Data1(1,point)-mod(Data1(1,point),2))/2;
Data(1,i-2)=mod(Data1(1,point),2);
point=point-1;
end
fprintf('转换成2进制:');disp(Data);
end
%生成龟壳矩阵
function tortoise=Tortoise()
tortoise(1,1)=6;
for i=2:256
tortoise(1,i)=mod(tortoise(1,i-1)+1,8);
end
for i=2:256
if mod(i,2)==0
tortoise(i,:)=mod(tortoise(i-1,:)-2,8);
else
tortoise(i,:)=mod(tortoise(i-1,:)-3,8);
end
end
end
%进行信息隐藏,带入当前两个像素值,返回信息隐藏点的行列
function [X,Y]=find(X,Y,number,tortoise)
%像素值0到255,龟壳矩阵1到256,需将两者对齐
X=double(X);Y=double(Y);
X=X+1;Y=Y+1;
%对边界进行特殊处理
if (X==1&&Y==1)||(X==256&&Y==1)||(X==1&&Y==256)||(X==256&&Y==256)||...
(X==1&&mod(Y,2)==1)||(X==256&&mod(Y,2)==1)||...
(Y==1&&(mod(X,4)==0||mod(X,4)==1))||(Y==256&&(mod(X,4)==2||mod(X,4)==3))
fprintf('该点在边界上 ');
if X==1&&Y==1 %判断其是否是龟壳矩阵的左上顶点
[X1,Y1,X2,Y2]=matrix(X,Y,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif X==256&&Y==1 %判断其是否是龟壳矩阵的左下顶点
[X1,Y1,X2,Y2]=matrix(X-2,Y,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif X==1&&Y==256 %判断其是否是龟壳矩阵的右上顶点
[X1,Y1,X2,Y2]=matrix(X,Y-2,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif X==256&&Y==256 %判断其是否是龟壳矩阵的右下顶点
[X1,Y1,X2,Y2]=matrix(X-2,Y-2,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif X==1&&mod(Y,2)==1 %判断其是否在龟壳矩阵上边界、是否需要边界处理
[X1,Y1,X2,Y2]=matrix(X,Y-1,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif X==256&&mod(Y,2)==1%判断其是否在龟壳矩阵下边界、是否需要边界处理
[X1,Y1,X2,Y2]=matrix(X-2,Y-1,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif Y==1&&(mod(X,4)==0||mod(X,4)==1)%判断其是否在龟壳矩阵左边界、是否需要边界处理
[X1,Y1,X2,Y2]=matrix(X-1,Y,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
elseif Y==256&&(mod(X,4)==2||mod(X,4)==3)%判断其是否在龟壳矩阵右边界、是否需要边界处理
[X1,Y1,X2,Y2]=matrix(X-1,Y-2,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
X=temp1;Y=temp2;
end
X=X-1;Y=Y-1; %将像素值恢复到0到255范围内
return;
end
%判断其是否是龟壳内部两点中的上内部点
if (tortoise(X,Y)==1 && tortoise(X+1,Y)==6)||(tortoise(X,Y)==3 && tortoise(X+1,Y)==0)||...
(tortoise(X,Y)==5 && tortoise(X+1,Y)==2)||(tortoise(X,Y)==7 && tortoise(X+1,Y)==4)
fprintf('该点在龟壳内 ');
[X,Y]=traversal(X-1,Y,number,tortoise);
X=X-1;Y=Y-1; %将像素值恢复到0到255范围内
return;
end
%判断其是否是龟壳内部两点中的下内部点
if (tortoise(X,Y)==6 && tortoise(X-1,Y)==1)||(tortoise(X,Y)==0 && tortoise(X-1,Y)==3)||...
(tortoise(X,Y)==2 && tortoise(X-1,Y)==5)||(tortoise(X,Y)==4 && tortoise(X-1,Y)==7)
fprintf('该点在龟壳内 ');
[X,Y]=traversal(X-2,Y,number,tortoise);
X=X-1;Y=Y-1; %将像素值恢复到0到255范围内
return;
end
%剩下的点全在龟壳的边上,且只有上下顶点两类
if mod(tortoise(X,Y),2)==1 %判断其是否在龟壳边的上顶点
fprintf('该点在龟壳边 ');
[X1,Y1]=traversal(X,Y,number,tortoise);
[X2,Y2]=traversal(X-2,Y-1,number,tortoise);
[X3,Y3]=traversal(X-2,Y+1,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
if (X3-X)^2+(Y3-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X3;temp2=Y3;
end
X=temp1;Y=temp2;
X=X-1;Y=Y-1; %将像素值恢复到0到255范围内
return;
end
if mod(tortoise(X,Y),2)==0 %判断其是否在龟壳边的下顶点
fprintf('该点在龟壳边 ');
[X1,Y1]=traversal(X-3,Y,number,tortoise);
[X2,Y2]=traversal(X-1,Y-1,number,tortoise);
[X3,Y3]=traversal(X-1,Y+1,number,tortoise);
temp1=X1;temp2=Y1;
if (X2-X)^2+(Y2-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X2;temp2=Y2;
end
if (X3-X)^2+(Y3-Y)^2<(temp1-X)^2+(temp2-Y)^2
temp1=X3;temp2=Y3;
end
X=temp1;Y=temp2;
X=X-1;Y=Y-1; %将像素值恢复到0到255范围内
return;
end
end
%从上顶点开始遍历一个龟壳,并返回需要寻找点的坐标
function [X,Y]=traversal(X,Y,number,tortoise)
if X<1||X>256||X+1<1||X+1>256||X+2<1||X+2>256||X+3<1||X+3>256||...
Y<1||Y>256||Y-1<1||Y-1>256||Y+1<1||Y+1>256
X=inf;Y=inf;
elseif tortoise(X,Y)==number
elseif tortoise(X+1,Y)==number
X=X+1;
elseif tortoise(X+1,Y-1)==number
X=X+1;
Y=Y-1;
elseif tortoise(X+1,Y+1)==number
X=X+1;
Y=Y+1;
elseif tortoise(X+2,Y)==number
X=X+2;
elseif tortoise(X+2,Y-1)==number
X=X+2;
Y=Y-1;
elseif tortoise(X+2,Y+1)==number
X=X+2;
Y=Y+1;
elseif tortoise(X+3,Y)==number
X=X+3;
end
end
%分别从左上顶点和右下顶点开始,遍历一个3*3矩阵,并返回需要寻找点的坐标
%分别从左上顶点和右下顶点开始遍历的作用是找出距离最小的点
function [X1,Y1,X2,Y2]=matrix(X1,Y1,number,tortoise)
flag=0;
X2=X1;Y2=Y1;
for i=0:1:2
for j=0:1:2
if tortoise(X1+i,Y1+j)==number
X1=X1+i;
Y1=Y1+j;
flag=1;
break;
end
end
if flag==1
break;
end
end
flag=0;
for i=2:-1:0
for j=2:-1:0
if tortoise(X2+i,Y2+j)==number
X2=X2+i;
Y2=Y2+j;
flag=1;
break;
end
end
if flag==1
break;
end
end
end
实验结果:


其中,生成的龟壳矩阵(部分)如下:

分析实验代码和结果,可以看到:
整个过程是先随机生成10个2进制数,并将其转换成8进制数,再进行信息隐藏,最后进行隐藏数据的提取,观察是否隐藏成功。
在该示例结果中,既有点在龟壳内部(第4个待隐藏值)也有点在龟壳边上(第1、2、3个待隐藏值),既有点对应的像素值不是待隐藏值(第1、3、4个待隐藏值)也有点刚好是待隐藏值(第2个待隐藏值)。实验结果显示,待隐藏信息全都顺利隐藏并且成功读取。
而且根据龟壳矩阵进行手动分析,可以验证整个实验过程是正确的。
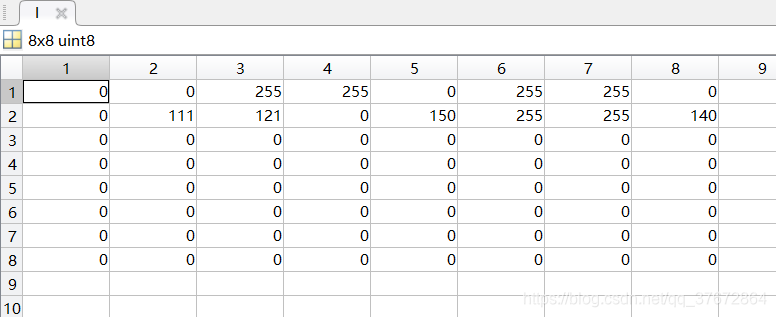
但是由于图像“coverlena.bmp”的特殊性,实验中并不会遇到点在边界上的情况。所以,我手动构造了一个特殊的8×![]() 8图像,以检查其边界的特判处理是否正确。
8图像,以检查其边界的特判处理是否正确。
这个图像包括:龟壳矩阵四个顶点(图像第1行)、龟壳矩阵上下左右四条边上随机各取一点(图像第2行)。图像具体像素值如下:
实验结果:

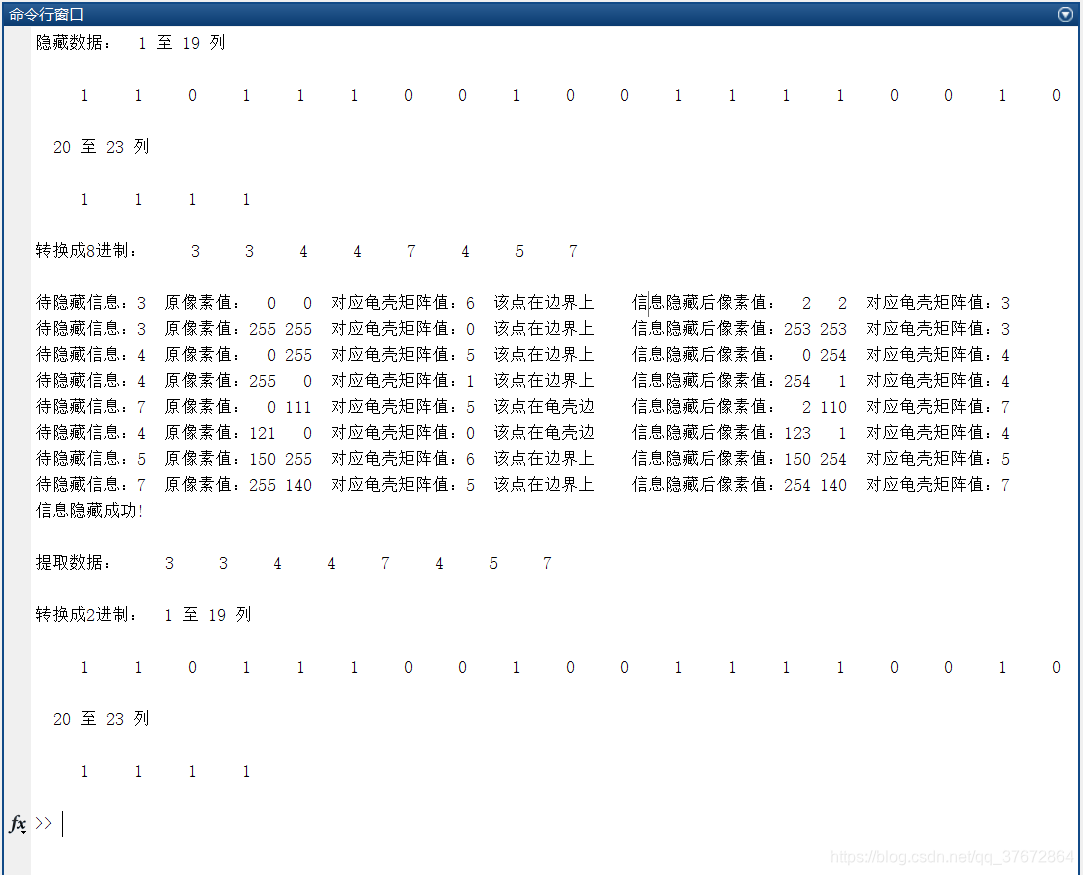
注意到其中第8、9个待隐藏信息显示在龟壳边上而不在边界上,这是因为虽然取的这八个点都是在龟壳矩阵的边上,却并不意味着需要进行“特判处理”即不在“边界”上,龟壳矩阵的四条边上也有一部分点是在龟壳上的。
实验结果显示,待隐藏信息全都顺利隐藏并且成功读取。根据龟壳矩阵进行手动分析,可以验证整个实验过程是正确的。
至此,对龟壳内、龟壳边和边界上的点都进行了测试,实验结果和手动验证都显示算法是正确的。
【小结或讨论】
基于龟壳的信息隐藏算法从本质上来说和EMD算法是一样的,都是利用魔术矩阵进行信息隐藏。但EMD的有一个很大的缺点,就是它隐藏的数据需要是5进制的,这无疑会使信息隐藏的效率变得低下。而基于龟壳的信息隐藏算法很好地解决了这个问题,它采用的是8进制的魔术矩阵,2进制同8进制的转换远比同5进制的转换有效率的多,而且使得每个信息隐藏点的容量进一步扩大到3bits。
基于龟壳的信息隐藏算法的基本原理:
龟壳矩阵是这个算法的基础,其中每个元素的值都在0-7之间,并且按照一定的差值规律排列,每一个龟壳都无冗余的包含了0-7的8个数。在进行信息隐藏时,先以图像中的两个像素值作为横、纵坐标来找到龟壳矩阵中对应的元素值,再在对应的龟壳中找到待隐藏信息值相同的点,以该点的横纵坐标替换掉数字图像中的原像素值。这样使得隐藏容量增加的同时,图像失真却保持很小。
当然效率的大幅提升必然会导致算法复杂度的提升。基于龟壳的信息隐藏算法和上一次实验的LSB和EMD算法相比难度大大增加,导致整个算法完整实现后,代码近300行。由于算法的复杂,我想在这里总结一下整个代码的构写思路和最核心的在龟壳中寻找待隐藏值的思路。
代码构写思路:
整个代码包含以下5个函数
1、Turtle_Shell()为主函数
2、Tortoise()作用是生成龟壳矩阵
3、find(X,Y,number,tortoise)作用是找到对应龟壳并找到待隐藏点,进行像素值替换。其中X为行数,Y为列数,number为待隐藏值,tortoise是已生成的龟壳矩阵。之所以将龟壳矩阵带入,是为了避免每次进行信息隐藏时都重新生成龟壳矩阵,从而降低代码运行效率。
4、traversal(X,Y,number,tortoise)作用是从上顶点开始遍历一个龟壳。其中X为该龟壳上顶点行数,Y为该龟壳上顶点列数。比较重要的一点是,若遍历龟壳不完整则返回无穷大,这是为了靠近边界处有时只需要遍历1个或2个龟壳而设立的。其他同上。
5、matrix(X1,Y1,number,tortoise)作用是分别从矩阵的左上顶点和右下顶点开始,遍历一个3×![]() 3矩阵,并返回需要寻找点的坐标。分别从两个起点的作用是两者遍历的路径刚好互补,从而若与待隐藏值相同的点有两个,可以找出距离最小的点。其他同上。
3矩阵,并返回需要寻找点的坐标。分别从两个起点的作用是两者遍历的路径刚好互补,从而若与待隐藏值相同的点有两个,可以找出距离最小的点。其他同上。
主函数Turtle_Shell控制整个流程,先调用Tortoise生成龟壳矩阵,再通过find函数进行信息隐藏。在find函数中,分类判断了待隐藏值的位置后,若在龟壳边/内则调用traversal遍历周围对应龟壳,若在边界则调用matrix遍历3×![]() 3矩阵,最终找到信息隐藏点并返回行列值。
3矩阵,最终找到信息隐藏点并返回行列值。
在龟壳中寻找待隐藏值的思路:
1、判断点在边界的特殊情况
(1)、四个顶点
(2)、龟壳矩阵第1行且列数为奇数(上边界特判)
(2)、龟壳矩阵第256行且列数为奇数(下边界特判)
(2)、龟壳矩阵第1列且行数为模4余0或1(左边界特判)
(2)、龟壳矩阵第256列且行数为模4余2或3(右边界特判)
2、判断点在龟壳内的情况
根据观察,整个魔术矩阵有4种龟壳,其内部两个值各不相同,分别为:<1,6>、<3,0>、<5,2>、<7,4>。若符合其中一种排列情况,说明其在龟壳内部。
3、判断点在龟壳边的情况
排除了以上两种情况后,该点则必在龟壳边上。根据分析,在龟壳边上的点实际上只有两类:龟壳上顶点和龟壳下顶点。
(1)、该点值为奇数则为龟壳上顶点
(2)、该点值为偶数则为龟壳下顶点
这次实验比较复杂,整个算法也是在不断地试错和分析中逐步完善的。实验过程中遇到过很多bug,比如我在将像素值和龟壳矩阵对齐时,遇见255+1始终等于255的奇怪现象。最后分析才发现,原来像素值默认为uint8格式,其表示的最大值就是255,最后将变量转换成double类型就解决了问题。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








